Continuité uniforme - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés
Fonctions lipschitziennes
Soit I un intervalle quelconque sur les nombres réels. Toute fonction k-lipschitzienne f de I dans l'ensemble des réels est uniformément continue.
En particulier, si f est dérivable et de dérivée bornée sur I, alors f est uniformément continue. En effet, si k est nul la fonction est constante et toute valeur de η satisfait la condition, sinon, ε/k est une valeur satisfaisante pour η.
Théorème de Heine
Le théorème de Heine indique que toute fonction continue d'un espace métrique dans un espace métrique est uniformément continue si l'ensemble de départ est compact.
En particulier, toute fonction continue d'un segment de l'ensemble des réels dans un espace métrique est uniformément continue.
Prolongement par continuité
Toute fonction uniformément continue à valeurs dans un espace complet se prolonge par continuité sur l' adhérence de son espace de départ (et ce, de façon unique).
Cette existence d'un prolongement continu découle du fait que l'image d'une suite de Cauchy par une application uniformément continue est une suite de Cauchy (l'unicité du prolongement continu, étant, elle, un fait général, de même que le fait que ce prolongement hérite de la continuité uniforme).
Cette propriété est utilisée parfois pour définir des fonctions comme l'intégrale ou l'exponentielle ou encore compléter des applications linéaires ou bilinéaires définies sur des espaces vectoriels normés.
Soient f une application uniformément continue, de F (un sous-ensemble de (E, d)) dans (G, δ), et (xn) une suite de Cauchy de F.
-
- La suite (f(xn)) est de Cauchy :
La fonction f est uniformément continue, c'est-à-dire :
![\forall \varepsilon > 0, \; \exists \eta >0, \; \forall x,y \in F, \quad [d(x,y)<\eta \Rightarrow \delta ( f(x),f(y))< \varepsilon]](https://upload.wikimedia.org/math/c/f/b/cfbe62973c575c025d69f5e9b95e5ffc.png) .
.La suite (xn) est de Cauchy, c'est-à-dire :
![\forall \eta > 0,\; \exists N \ge 0,\; \forall n,m \in\N \quad [(n>N \;\text{et}\; m>N )\Rightarrow d(x_n,x_m)<\eta ]](https://upload.wikimedia.org/math/b/5/1/b511475e5b4570afaa7f8bfe1f9fa1f4.png) .
.Ces deux propriétés montrent que :
![\forall \varepsilon > 0, \; \exists N \ge 0, \; \forall n,m \in \N \quad [(n>N \;\text{et}\; m>N )\Rightarrow \delta ( f(x_m),f(x_m))< \varepsilon]](https://upload.wikimedia.org/math/b/4/5/b4571602ee07a245d31723bea076f05f.png) .
.autrement dit la suite (f(xn)) est de Cauchy.
Soit A l'adhérence de F et G est maintenant supposé complet.
-
- La fonction f se prolonge en une application uniformément continue sur A :
Soit a un élément de A et (xn) une suite d'éléments de F convergeant vers a. La suite est de Cauchy car elle converge. La proposition précédente montre que la suite (f(xn)) est de Cauchy, donc convergente puisque G est complet. Soit (yn) une autre suite convergeant vers a, la suite (f(yn)) est aussi convergente. Montrons que les deux limites sont les mêmes. Soit la suite (zn) définie par : z2n=xn et z2n+1=yn. Pour les mêmes raisons que précédemment, la suite (f(zn)) converge. Or sa limite est égale à celle de toute suite extraite, donc à celles de (f(xn)) et (f(yn)), ce qui montre bien que ces deux limites sont égales.
Cela permet de définir g comme l'application de A dans G qui à a associe la limite de la suite (f(xn)) où (xn) est n'importe quelle suite d'éléments de F convergeant vers a. En particulier pour a appartenant à F on peut choisir xn=a, donc g(a)=f(a), donc g est bien un prolongement de f.
Montrons que g est uniformément continue. Soit ε un réel strictement positif, l'uniforme continuité de f sur F montre l'existence d'un réel strictement positif η tel que :
![\forall x,y\in F,\quad [d(x,y) < \eta \ \Rightarrow \ \delta(f(x),f(y))<\varepsilon]\!](https://static.techno-science.net/illustration/Definitions/autres/0/0c2fd3b1ee9e698aa15031e67b8c082c_af55284b375e741aa00bd76a071f26e6.png)
Soient a et b deux éléments de A à une distance strictement inférieure à η l'un de l'autre et soit (an) (resp. (bn)) une suite d'éléments de F convergeant vers a (resp. b). On a donc
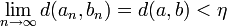
si bien que pour n suffisamment grand, d(an,bn)<η et par conséquent δ(f(an),f(bn))<ε, donc (par passage à la limite) δ(g(a),g(b))≤ε.
Cela démontre l'uniforme continuité de g sur A.
















































