Construction du pentagone régulier à la règle et au compas - Définition

Introduction

La construction d'un pentagone régulier à la règle et au compas est une des premières constructions (après le triangle équilatéral et le carré) non triviale réalisable grâce aux axiomes d'Euclide. La construction exacte d'un pentagone régulier fait intervenir le nombre d'or et surtout son pendant géométrique : le triangle d'or. Euclide propose une construction d'un pentagone régulier inscrit dans un cercle donné. Mais d'autres méthodes de construction plus rapides existent et sont exposées ci-dessous.

D'autres mathématiciens ou géomètres proposent aussi des constructions approchées réalisables avec un seul écartement de compas. C'est le cas par exemple d'Abu l-Wafa dans son Livre sur l’indispensable aux artisans en fait de construction (X^e siècle), ou de Matthaüs Roritzer dans sa Geometria deutsch (1486), construction qu'Albrecht Dürer reprend dans son Instructions pour la mesure, à la règle et au compas, des lignes, plans et corps solides (1525)

Construction selon Euclide

Euclide construit un pentagone régulier (équilatéral et équiangle) inscrit dans un cercle. Son élément de base est le triangle d'or : un triangle isocèle dont les angles avec la base sont double de l'angle au sommet (et ainsi l'angle au sommet est le 5^e de l'angle plat). 180/5=36

Construction du triangle d'or

Dans la figure jointe, I est le milieu de [AC], AC = AB, IB = ID, AD = AE = BF. Euclide démontre que le triangle ABF est un triangle d'or en utilisant des propriétés assez longues

• AE² = BA × BE
• Puissance d'un point par rapport au cercle circonscrit à AEF
• Théorème de l'angle inscrit dans ce même cercle.

De nos jours, la démonstration est plus simple car si on note AC = 1, on obtient

• grâce au théorème de Pythagore
• où est le nombre d'or

Les dimensions du triangle ABF sont donc 1 - 1 - . C'est bien un triangle d'or.

Construction du pentagone

Euclide prouve qu'il peut construire un triangle d'or dans un cercle.

1. À partir du triangle d'or OA'C construire le triangle d'or CDA grâce à l'arc de cercle de centre A' et de rayon A'C
2. En prenant les bissectrices des angles C et D en les prolongeant jusqu'au cercle, il obtient les deux sommets B et E manquant.

Pentagone approché

Méthode de Dürer

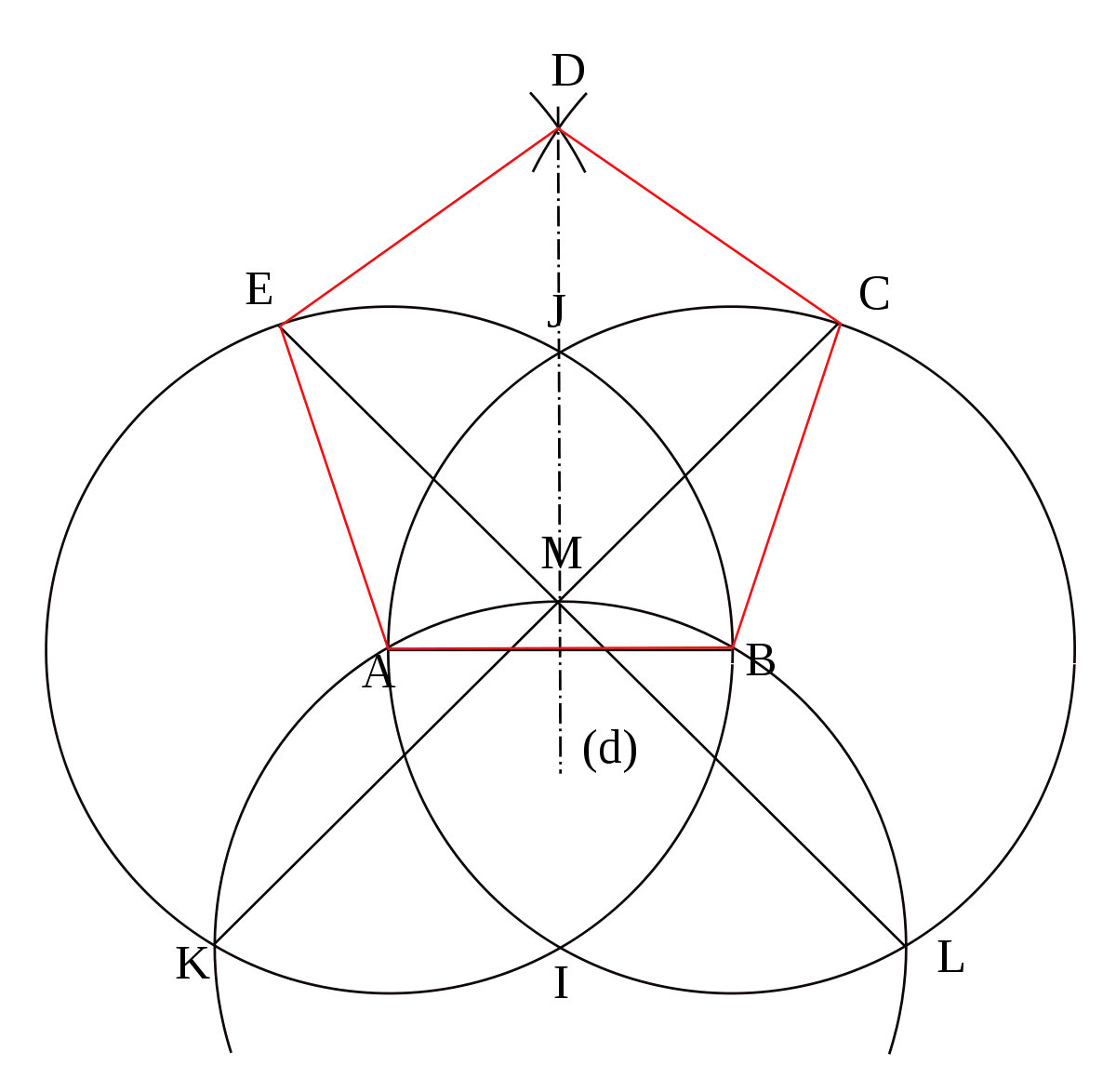
Dans son livre ''Instructions pour la mesure, à la règle et au compas, des lignes, plans et corps solides, Albert Dürer propose cette construction qu'il estime exacte. L'intérêt de cette construction vient du fait de l'économie de moyens mis en œuvre: tous les cercles tracés ont même rayon.

Cependant, le pentagone tracé est bien équilatéral mais il n'est pas équiangle : les angles de base font environ 108,35 ° au lieu des 108° attendus et l'angle au sommet fait un peu plus de 109° . Cette preuve est apportée par les géomètres Giovanni Battista Benedetti et Clavius .

1. Tracer le segment [AB] et la médiatrice (d) de ce segment.
2. Tracer les cercles de rayon AB de centres A et B. Ils se coupent en I et J
3. Tracer un cercle de centre I et de rayon AB. Il coupe les cercles précédents en K et L et la droite (d) en M. les droites (KM) et (LM) recoupent les cercles en C et E
4. D est tel que CD = ED = AB

Avec découpage de segments

pentagone régulier inscrit

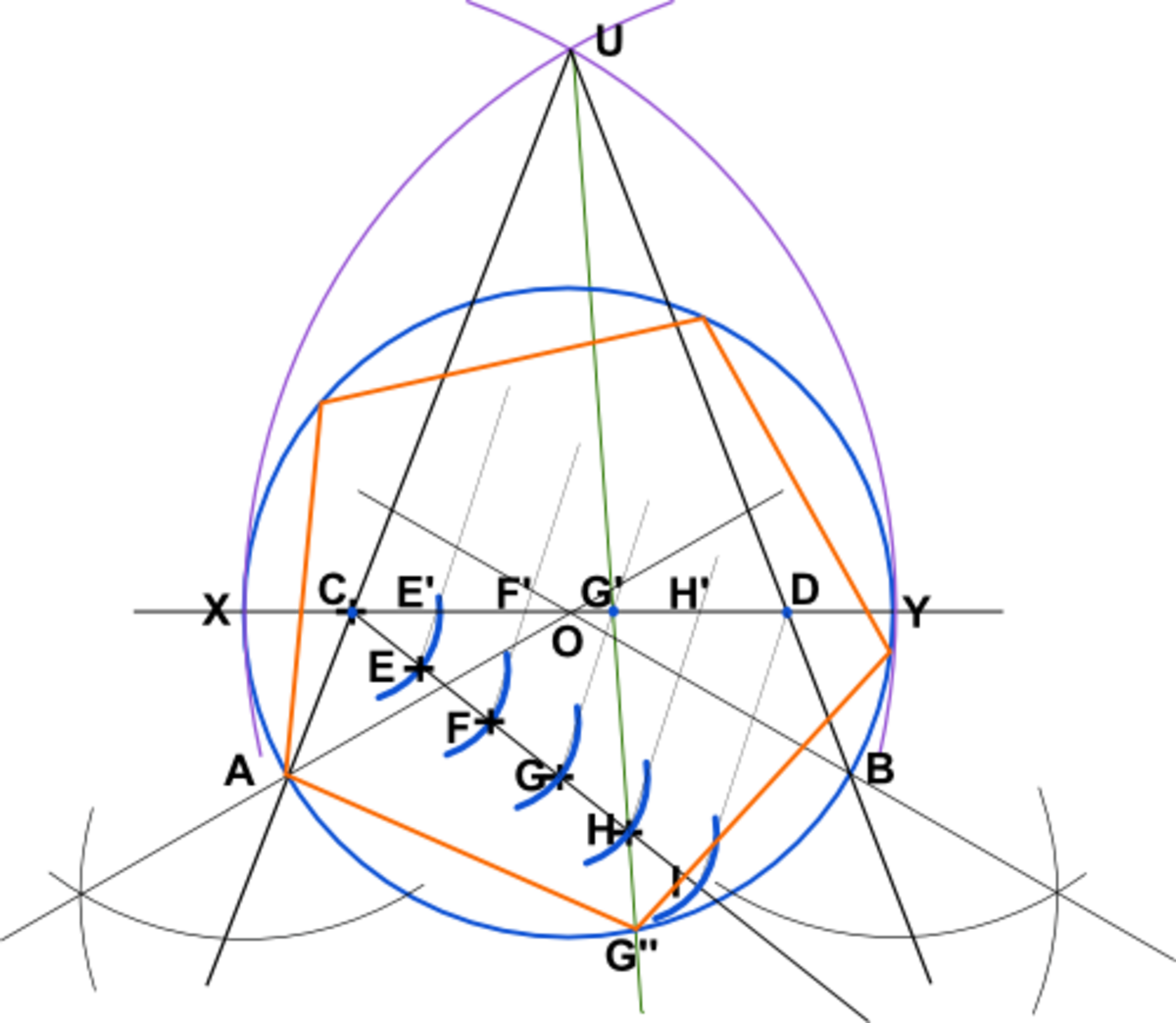
En s'inspirant de la construction de l'enneagone, on peut tracer une construction approchée d'un pentagone régulier, à la règle et au compas, selon la méthode identique à celle donnée pour l'heptagone.

Tracer le cercle de centre O de rayon OX, avec un angle OÂB = 120°.

Tracer l'arc de cercle de rayon XY et de centre X

Tracer l'arc de cercle de rayon YX et de centre Y

Ces arcs se coupent en U

Tracer les droites (UA) et (UB). Ils coupent le diamètre (XY) en C et D

A partir de C, sur une droite quelconque, porter avec un compas cinq segments égaux CE = EF = FG = GH = HI

Tracer la droite ( ID) et tracer la parallèle à celle-ci passant par G (au moyen de la règle et du compas). Elle coupe (XY) en G’.

Tracer la droite (UG').Elle coupe le cercle en G’’.

Reportez au compas tout le long du cercle la longueur AG’’, on trouve alors les cinq sommets du pentagone régulier inscrit dans le cercle.

Remarque : pour faire un pentagone comprenant le point B, il aurait fallu prendre le point F’.

Par cette construction, l'angle au centre AOG’’est d'environ 72,14 degré au lieu des 72 attendus, soit une erreur relative de 1,92 pour mille.

Cette méthode permet de faire n'importe quel polygone régulier. Il suffit de sectionner le segment CD en autant de secteurs identiques qu'il y a de côtés souhaités pour le polygone. Ensuite, on prend le troisième point en partant de C (G’), on trace le segment qui le relie à U et on obtient G’’ à l'intersection entre le cercle et ce segment (dans le demi-plan inférieur à XY). L'erreur commise sur l'angle au centre pour cette méthode varie de 1,92 pour mille à 11,7 pour mille selon le nombre de côtés.