Construction des nombres réels - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, il existe différentes constructions des nombres réels, dont les deux plus connues sont
- les coupures de Dedekind,
- les suites de Cauchy.
Construction intuitive à partir des nombres décimaux
Un nombre réel est une quantité qui a pour représentation décimale x = n + 0.d1d2d3..., où n est un entier, chaque di est un chiffre entre 0 et 9, et la séquence ne se termine pas par une infinité de 9. La définition de x est alors le nombre qui satisfait cette double inéquation pour tout k :
Cette construction, outre son manque de rigueur sous cette forme, présente divers inconvénients, dont le plus important est la difficulté de donner des algorithmes simples pour la multiplication, et même pour l'addition dans des cas tels que 
.
Construction via les suites de Cauchy
Cette construction est plus difficile à aborder mais la construction des opérations y est plus naturelle. Cette méthode est analogue, formellement, à la méthode de construction qui permet, à partir d'un espace métrique E, d'obtenir un espace métrique complet E' tel que E soit dense dans E' .
Comment et pourquoi parler de suites de Cauchy
Il ne saurait être question, sous peine de cercle vicieux, de définir a priori, sur un corps totalement ordonné K, une distance à valeurs dans ... 
, que l'on n'a pas encore défini ! Les deux notions de suite de Cauchy et de suite convergente sont donc à prendre (ici, mais surtout dans le paragraphe "Équivalence des deux constructions") non pas au sens usuel de suite de Cauchy et de suite convergente dans un espace métrique, mais au sens suivant : une suite 
dans K
- est de Cauchy si
- converge vers un élément a si
où pour tout 
, l'élément 
désigne le plus grand des deux éléments x et − x.
Ces deux définitions de suites de Cauchy et de suites convergentes - qui sur correspondront a posteriori aux définitions usuelles - sont celles liées respectivement à la structure uniforme sur le groupe ordonné (K,+,
) et à la topologie de l'ordre qu'elle induit. La complétude d'un espace uniforme implique la convergence de ses suites de Cauchy. La réciproque, fausse en général, est vraie si le corps K est archimédien (et le sera). Ceci fournira un critère simple pour montrer que est complet (en tant qu'espace uniforme) avant même de l'avoir muni de sa structure usuelle d'espace métrique. On utilisera de plus constamment que si K est archimédien alors les 
qui interviennent dans ces définitions peuvent toujours être pris dans 
.
Définition en tant qu'ensemble
L'idée de Cantor (et quelques années avant lui de Méray) réside dans le fait que l'on peut atteindre tout nombre réel par une suite de Cauchy de 
. L'élément limite auquel il va falloir donner un sens sera alors défini comme un nombre réel. L'ensemble des suites de Cauchy de , que nous noterons 
, apparaît cependant bien trop vaste. En effet, par exemple pour un rationnel donné, il existe une infinité de suites de Cauchy convergeant vers cette limite. Il est nécessaire de quotienter cet ensemble par une relation d'équivalence 
entre les suites : deux suites de Cauchy de rationnels seront dites équivalentes si leur différence converge vers 0 (la convergence d'une suite dans ayant le sens défini ci-dessus, de même que la propriété d'être de Cauchy) vers 0 :
Cette relation est bien une relation d'équivalence : elle est
- réflexive car la suite nulle converge bien vers 0,
- symétrique car si une suite converge vers 0, alors la suite opposée converge aussi vers 0,
- transitive en raison de l'inégalité triangulaire sur la valeur absolue dans 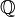. Si (un), (vn) et (wn) sont trois suites de rationnels, nous avons en effet :
On définit alors comme l'ensemble des classes d'équivalence de suites de Cauchy de rationnels (pour cette relation d'équivalence sur ).
Opérations
L'ensemble des suites dans est naturellement muni d'une structure d'anneau commutatif avec l'addition et la multiplication héritées de la structure de corps de . Si (un) et (vn) sont deux suites, alors ces opérations sont définies par :
Ces opérations conservent le critère de Cauchy, c'est-à-dire que la somme et le produit de deux suites de Cauchy sont encore des suites de Cauchy. Dans l'anneau des suites à valeurs rationnelles, le sous-ensemble est donc un sous-anneau.
Dans cet anneau , le sous-ensemble des suites qui convergent vers 0 est un idéal (c'est-à-dire que la somme de deux suites qui convergent vers 0, et le produit d'une suite qui converge vers 0 par une suite de Cauchy, convergent vers 0). La relation d'équivalence apparaît dès lors comme celle associée à cet idéal, ce qui permet de munir d'une structure d'anneau quotient (encore commutatif et unitaire).
On plonge dans via les suites stationnaires. On notera (a) la classe contenant la suite constante égale à 
.
L'anneau quotient
est un corps.
Il s'agit de montrer que tout nombre réel non nul admet un inverse. Soient a un élément de différent de (0) et 
une suite de cette classe a. Dire que la classe a est différente de la classe (0) c'est dire que la suite ne converge pas vers 0, ce qui s'écrit :
ou encore : pour un certain 
, il y a une infinité de termes de la suite qui ont une valeur absolue plus grande que . Comme cette suite est de Cauchy, à partir d'un certain rang N, la valeur absolue de la différence de deux termes est plus petite que 
. On en déduit, en utilisant (1) :
Soit la suite (bn) définie par 
si 
et bn = 0 (par exemple) sinon. Cette suite de rationnels est de Cauchy, car d'après (2),
On peut donc considérer sa classe b dans , et l'on a
Ordre
On définit 
comme le sous-ensemble des classes contenant au moins une suite de Cauchy à valeurs dans 
(l'ensemble des rationnels positifs ou nuls), puis on définit une relation d'ordre total sur en posant
Le fait que cette relation soit réflexive et transitive est immédiat. Qu'elle soit également antisymétrique (donc définisse bien un ordre) résulte du fait que 
. Que cet ordre soit total vient de 
.
On a ainsi muni le corps d'une structure de corps totalement ordonné. En effet, cet ordre est compatible avec l'addition (par construction) mais aussi avec la multiplication (car est clairement stable par produits). On remarque que cette relation d'ordre coïncide, sur 
(plongé dans comme déjà mentionné), avec la relation d'ordre usuelle.
On démontre de plus que est archimédien. On peut donc conclure :
est un corps totalement ordonné archimédien.
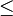- est antisymétrique :
Il s'agit de prouver que . Soient 
tels que a = − b, montrons que a = (0). Il existe deux suites de Cauchy (an), (bn) de rationnels positifs ou nuls représentant respectivement a et b. Alors a + b = (0) se traduit par : (an + bn) converge vers 0 dans , ce qui (puisque 
) entraîne que (an) converge aussi vers 0, si bien que a = (0).
- L'ordre 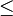est total :
Il s'agit de prouver que . Soient 
et (an) une suite de Cauchy de rationnels représentant cette classe. Si cette suite admet une infinité de termes positifs ou nuls, comme la sous-suite correspondante représente la même classe, 
. Même chose en remplaçant "positifs" par "négatifs" et par 
. Or ces deux cas (non exclusifs) recouvrent toutes les possibilités.
- est archimédien :
Il s'agit de montrer que, pour tous réels 
et 
, il existe un entier 
tel que 
. Il suffit de poser 
. Le réel x a pour représentant (xn) suite de Cauchy rationnelle donc majorée. On prend un majorant N entier de cette suite. Pour tout entier n, on a alors 
donc 
donc 
donc .
Complétude
Sur , l'ordre qu'on vient de définir donne un sens aux notions de suite de Cauchy et de suite convergente. On va montrer que tout réel est limite d'une suite de rationnels. Plus précisément : si une suite de Cauchy de rationnels (an) représente un réel a alors la suite de réels ((an)) converge dans vers a. Ainsi, toutes les suites de Cauchy de rationnels convergent dans . On va montrer que c'est aussi le cas pour toute suite de Cauchy de réels :
- Toute suite de Cauchy de rationnels converge dans vers sa classe :
On utilisera les majuscules pour désigner les réels et les minuscules pour désigner les rationnels. Soient (an) une suite de Cauchy de rationnels, A sa classe, et (pour tout entier n) An le réel représenté par la suite constante an. On cherche, pour un rationnel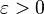 
fixé, à prouver l'existence d'un entier N tel que
Il suffit pour cela d'appliquer le critère de Cauchy à la suite (an), en remarquant que si 
alors pour tout , la suite de rationnels 
est positive ou nulle à partir du rang N donc la classe 
qu'elle représente est dans .
- Dans , toute suite de Cauchy converge :
Soit (Un) une suite de Cauchy de réels, il s'agit de prouver que cette suite converge dans . On a vu précédemment que tout réel est limite de rationnels. On peut donc choisir, pour tout entier n>0, un rationnel an tel que 
. La suite (Un − an) converge alors vers 0. La suite (an) est donc, comme (Un), de Cauchy. On peut donc considérer sa classe : notons U ce réel. Puisque (an) converge vers U et que (Un − an) converge vers 0, la suite (Un) converge vers U.