Constante gravitationnelle - Définition
La liste des auteurs de cet article est disponible ici.
Comparaison avec les autres forces fondamentales
Quand on compare les quatre forces fondamentales (force de gravitation, force électromagnétique, force faible, force forte), il apparait que la force de gravitation est extrêmement plus faible que les autres. Par exemple, la force de gravitation entre un électron et un proton séparés par un mètre serait d'environ 10-67 newton, tandis que la force électromagnétique entre les deux mêmes particules à la même distance serait d'environ 10-28 newton, c'est-à-dire 39 ordres de grandeur (ou 1039 fois) plus importante.
Les dimensions de
La valeur de
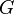
Cependant, cette valeur a une signification fondamentale selon les unités de Planck : la constante gravitationnelle est égale numériquement et aussi dimensionnellement au cube de la longueur de Planck, divisé par la masse de Planck et le carré du temps de Planck.
Finalement, ce sont ces unités de Planck qui sont les plus fondamentales, puisqu'elles représentent les plus petites quantités ayant un sens dans la physique moderne (et notamment la physique quantique).
En d'autres termes, on pourrait dire que
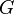
Constantes associées
Le paramètre gravitationnel standard
Le produit
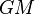
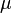
Ce paramètre fournit une simplification pratique des différentes formules liées à la gravitation.
Selon que
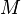
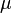
En fait, pour la Terre et le Soleil, ce produit est connu avec une plus grande précision que celle associée à chacun des deux facteurs
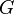
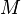
- Pour la Terre :
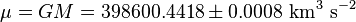
La constante gravitationnelle de Gauss
De même, les calculs de la mécanique céleste peuvent être faits dans les unités de masse solaire plutôt que celles du Système international d'unités, comme le kilogramme.
Dans ce cas, on utilise la constante gravitationnelle de Gauss, qui se note
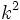
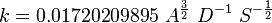
avec :
-
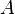
-
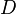
-
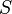
Si à la place du jour solaire moyen, on utilise l'année sidérale comme unité de temps, la valeur de