Conjugué - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, le conjugué d'un nombre complexe z est le nombre complexe formé de la même partie réelle que z mais de partie imaginaire opposée.
Définition
Le conjugué d'un nombre complexe ![]() , où a et b sont réels, est
, où a et b sont réels, est ![]() (lu « z barre ») mais est très souvent noté aussi z * ,
(lu « z barre ») mais est très souvent noté aussi z * ,
Dans le plan, le point d'affixe ![]() est le symétrique du point d'affixe
est le symétrique du point d'affixe ![]() par rapport à l'axe des abscisses.
par rapport à l'axe des abscisses.
Le module du conjugué reste inchangé.
On peut définir une application, appelée conjugaison, par
La conjugaison est une opération linéaire qui est de plus continue. C'est de plus un automorphisme de corps de ![]() dans lui-même.
dans lui-même.
Quaternions
Le conjugué du quaternion ![]() est
est ![]() .
.
Propriété
- On peut calculer aisément l'inverse d'un quaternion en utilisant les propriétés du quaternion conjugué.
Propriétés
On prend ![]() .
.
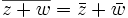
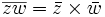
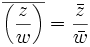 si
si 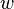 est non nul
est non nul- si
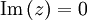 alors
alors 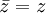
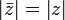
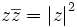
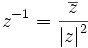 pour z non-nul.
pour z non-nul.
Populaires