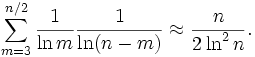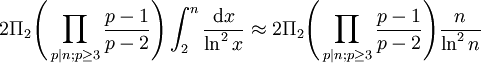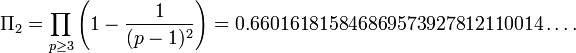Conjecture de Goldbach - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La conjecture de Goldbach stipule que tout nombre entier pair strictement supérieur à 2 peut être écrit comme la somme de deux nombres premiers (le même nombre premier pouvant être utilisé plusieurs fois). C'est l'un des plus vieux problèmes non résolus de la théorie des nombres et des mathématiques.
Par exemple,
- 4 = 2 + 2
- 6 = 3 + 3
- 8 = 3 + 5
- 10 = 3 + 7 = 5 + 5
- 12 = 5 + 7
- 14 = 3 + 11 = 7 + 7
- etc.
Une formulation équivalente via une division par deux :
Tout nombre entier strictement supérieur à 1 est la moyenne de deux nombres premiers.
Origine
En 1742, le mathématicien prussien Christian Goldbach écrivit une lettre au mathématicien suisse Leonhard Euler dans laquelle il proposait la conjecture suivante :
Tout nombre supérieur ou égal à 3 peut être écrit comme une somme de trois nombres premiers.
(Goldbach admettait 1 comme nombre premier; la conjecture moderne exclut 1, et remplace donc 3 par 6)
Ceci est équivalent à ce que tout nombre pair supérieur ou égal à 4 soit somme de deux nombres premiers impairs:
- n'importe quel nombre supérieur ou égal à 6 peut être obtenu en ajoutant 2 ou 3 à un nombre pair supérieur ou égal à 4.
- inversement, pour tout entier pair n supérieur ou égal à 4, si n+2 peut s'écrire comme somme de trois nombres premiers, l'un d'eux est nécessairement pair, donc égal à 2, donc n est somme de deux nombre premiers.
Une version plus faible de la conjecture stipule simplement que tout nombre impair supérieur ou égal à 9 est somme de trois nombres premiers impairs.
État des recherches
Cette conjecture a fait l'objet de recherches par plusieurs théoriciens des nombres et a été vérifiée par ordinateur pour tous les nombres pairs jusqu'à
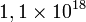
Nous savons que tout nombre pair peut être écrit comme une somme d'au plus six nombres premiers. Comme conséquence du travail de Vinogradov, nous pouvons affirmer que tout nombre pair suffisamment grand peut être écrit comme la somme d'au plus quatre entiers premiers. Vinogradov a montré de plus que presque tout nombre pair peut être écrit comme la somme de deux nombres premiers (dans le sens que la proportion des nombres pairs qui peuvent s'écrire sous cette forme tend vers 1). En 1966, Chen Jingrun a montré que tout nombre pair suffisamment grand peut être écrit comme somme d'un nombre premier et d'un nombre ayant au plus deux facteurs premiers.
Afin de faire de la publicité pour le livre Uncle Petros and Goldbach's Conjecture de Apostolos Doxiadis, l'éditeur britannique Tony Faber offrit un prix de 1 000 000 $ pour une preuve de la conjecture en 2000. Le prix ne pouvait être attribué qu'à la seule condition que la preuve soit soumise à la publication avant avril 2002. Il n'a jamais été réclamé.
La conjecture de Goldbach est un cas particulier d'une conjecture liée à l'hypothèse H de Schinzel.
Justification heuristique
La majorité des mathématiciens pense que la conjecture de Goldbach est vraie, surtout sur des considérations statistiques axées sur la répartition probabiliste des nombres premiers : plus le nombre est grand, plus il y a de manières disponibles pour le représenter sous forme de somme de deux ou trois autres nombres, et la plus « compatible » devient celle pour qui au moins une de ces représentations est constituée entièrement de nombres premiers.
Une version très grossière de l'argument probabiliste heuristique (pour la forme forte de la conjecture de Goldbach) est la suivante. Le théorème des nombres premiers affirme qu'un entier
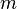
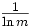
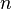
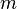
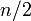
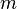
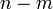
-
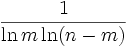
Cet argument heuristique n'est pas rigoureux pour de nombreuses raisons ; par exemple, il est supposé que les éventualités que
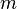
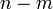
Puisque cette quantité tend vers l'infini lorsque n augmente, nous pouvons espérer que chaque grand entier pair n'a pas qu'une seule représentation sous forme de somme de deux nombres premiers, mais en fait possède beaucoup plus de telles représentations.
L'argument heuristique ci-dessus est en fait quelque peu imprécis, car il ignore certaines corrélations entre les probabilités que
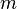
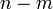
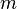
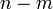
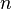
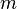
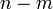
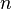
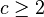
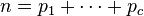
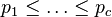
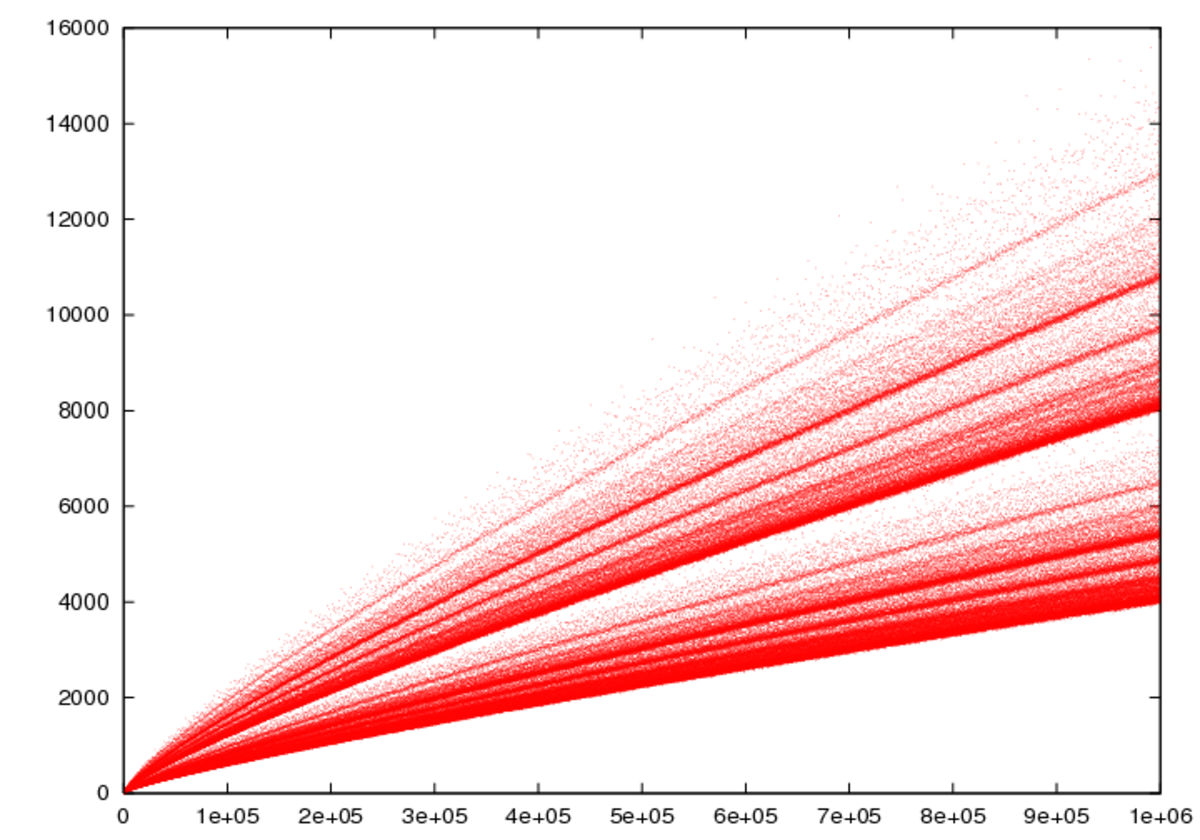
où le produit couvre tous les nombres premiers
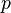
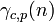
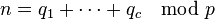
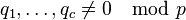
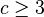
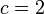
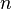
lorsque
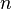
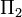
Cette formule asymptotique est quelquefois connue comme la conjecture étendue de Goldbach. La conjecture forte de Goldbach est en fait très similaire à la conjecture des nombres premiers jumeaux, et les deux conjectures sont reconnues comme étant globalement de difficulté comparable.