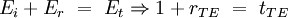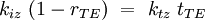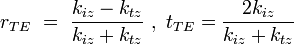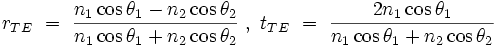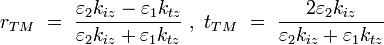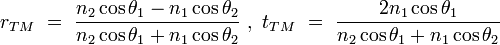Coefficients de Fresnel - Définition

Calculs des coefficients dans le cas général

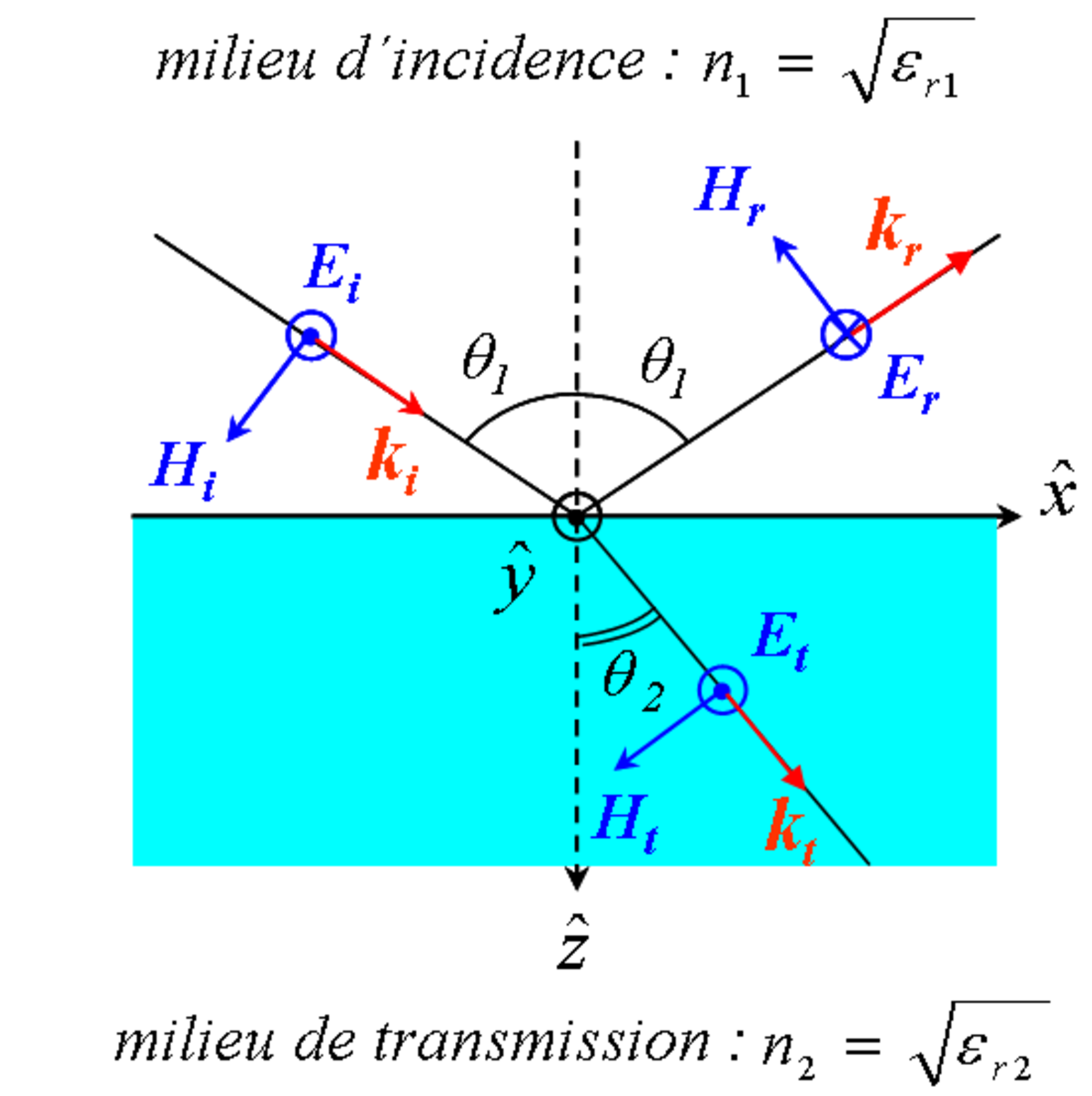
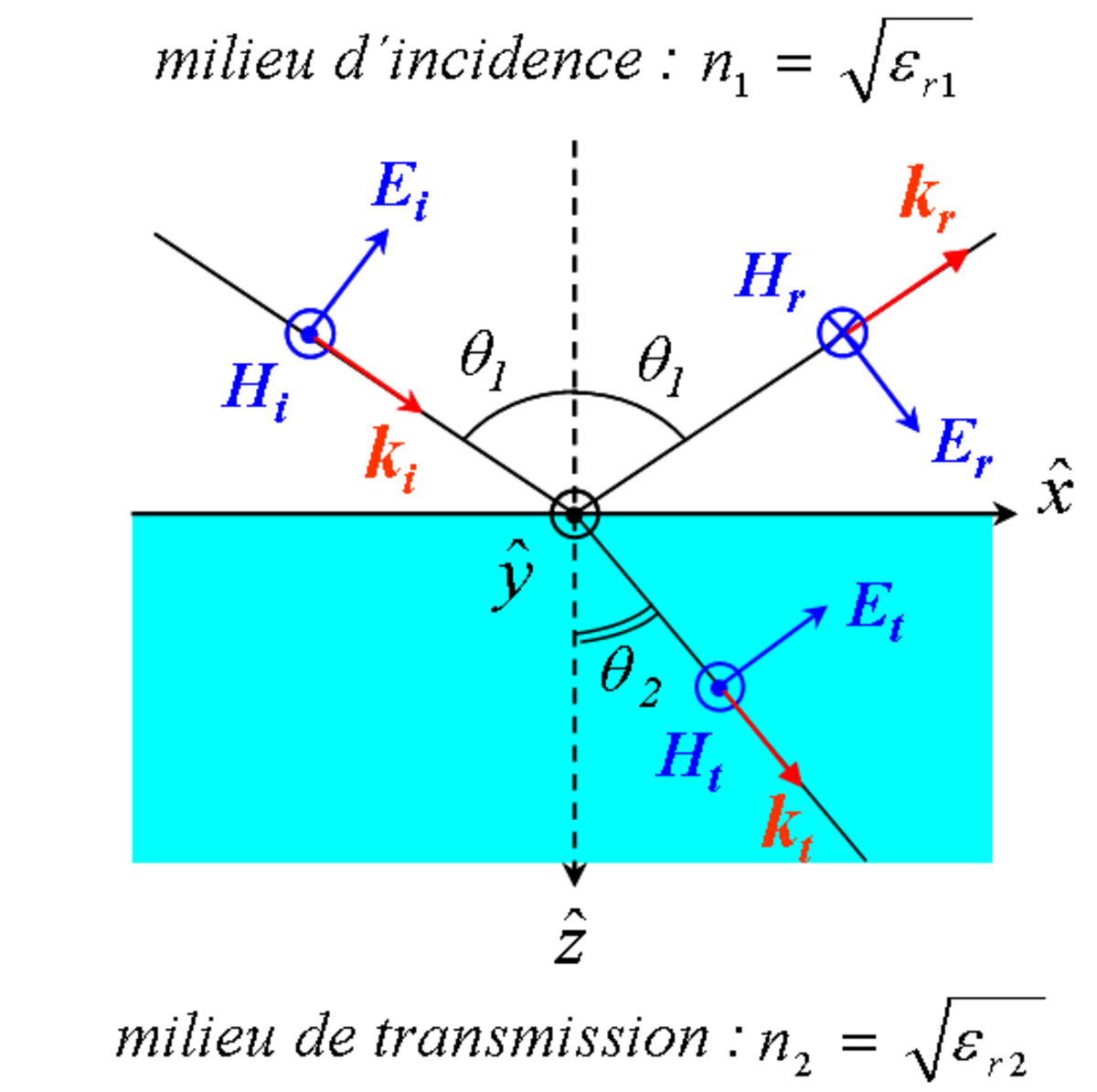
Considérons 2 milieux, d'indices de réfraction différents, séparés par une interface plane.

Hypothèses de travail

L'onde incidente est une onde plane, de vecteur d'onde , et de pulsation ω.

Les coefficients de Fresnel calculés ici ne sont valables que sous les hypothèses suivantes sur les milieux :

• Ils sont non magnétiques.
• Ils sont linéaires, homogènes et isotropes.

On rajoute aussi une hypothèse de calcul à savoir l'hypothèse harmonique qui consiste à considérer les grandeurs électromagnétiques à une fréquence particulière, et à les noter comme les parties réelles de grandeurs complexes. Ceci simplifie les calculs et permet aussi de déduire des équations de manière esthétique des phénomènes électromagnétiques comme l'absorption, le déphasage de l'onde, les ondes évanescentes...

Les coefficients de Fresnel dépendent de la polarisation du champ électromagnétique, on considère en général 2 cas:

• Transverse électrique (TE): le champ électrique incident est polarisé perpendiculairement au plan d'incidence, le champ magnétique est contenu dans le plan d'incidence.
• Transverse magnétique (TM): le champ magnétique incident est polarisé perpendiculairement au plan d'incidence, le champ électrique est contenu dans le plan d'incidence.

Cas des ondes transverses électriques

Champ électrique polarisé perpendiculairement au plan d'incidence

Considérons une onde plane électromagnétique :

où E représente l'amplitude complexe

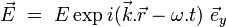
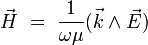
Dans le cas où le champ électrique incident est polarisé perpendiculairement au plan d'incidence, la composante tangentielle du champ électrique et magnétique sont continues:

Les coefficients de transmission et de réflexion s'écrivent alors :

En introduisant, pour chaque milieu, la relation de dispersion , on obtient les coefficients de Fresnel en fonction des caractéristiques de l'incidence (n₁,θ₁) et de la réfraction (n₂,θ₂) :

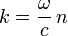
Discussion : les indices de réfraction étant complexes, la polarisation de l'onde transmise et réfléchie peut être modifiée par rapport à l'onde incidente. Même dans le cas où ces indices seraient réels, dans le cas , il se peut que le coefficient de réflexion devienne négatif, l'onde réfléchie est alors déphasée de 180° par rapport à l'onde incidente (voir figure).
La seule façon d'annuler le coefficient de réflexion est, en tenant compte des Lois de Snell-Descartes, d'avoir n₁ = n₂. Par conséquent, une onde polarisée transverse électrique subit une réflexion dès qu'elle passe dans un milieu d'indice optique différent, ce qui n'est pas le cas d'une onde transverse magnétique (existence d'un Angle de Brewster).

Cas des ondes transverses magnétiques

Champ magnétique polarisé perpendiculairement au plan d'incidence

En introduisant, pour chaque milieu, la relation de dispersion , on obtient les coefficients de Fresnel en fonction des caractéristique de l'incidence (n₁,θ₁) et de la réfraction (n₂,θ₂) :

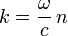
Remarque : suivant les ouvrages, les signes des coefficients de Fresnel diffèrent. Ceci provient des orientations arbitraires faites au départ. Par exemple, orienter sur la figure H_r vers l’avant, revient à remplacer, pour le calcul de r, E_r par -E_r ce qui changera le signe du coefficient. Dans le calcul de filtres interférentiels, on tiendra compte des coefficients de Fresnel pour calculer le déphasage à la réflexion entre les couches du filtre.

Discussion : le cas TM est remarquable à deux titres :

• le coefficient de réflexion peut devenir nul pour un angle d'incidence, dit angle de Brewster;
• dans certaines situations (interface métal-air), le dénominateur du coefficient de réflexion TM peut devenir nul (le coefficient devient infini !). On obtient alors une onde réfléchie et une onde transmise sans onde incidente : l'étude du dénominateur précise alors les conditions de réalisation, les composantes des vecteurs d'ondes sont alors imaginaires. Le processus emploie donc les ondes évanescentes, et provoque l'apparition des plasmons de surface.