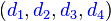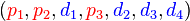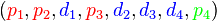Code de Hamming (7,4) - Définition
La liste des auteurs de cet article est disponible ici.
Construction du code
Code linéaire
Un code linéaire dispose d'une structure algébrique plus riche que celle du cadre général des codes correcteurs. L'ensemble E des messages à envoyer est celui de mots de quatre lettres prises dans l'ensemble {0,1}, le message est codé en un mot de sept lettres encore prises dans le même ensemble. On note F l'espace des mots de sept lettres binaires. E et F peuvent être considérés comme des espaces vectoriels sur le corps binaire {0,1}. Les tables d'addition et de multiplication sont les suivantes:
|
|
L'addition est intéressante car la somme d'une suite de valeurs est égale zéro dans le corps si la somme est paire dans les entiers et un sinon. La multiplication est habituelle, multiplier par zéro donne toujours zéro et multiplier par un ne modifie pas la valeur.
L' encodage, c’est-à-dire l'opération consistant à transformer le message de E de quatre lettres en un code de F de sept lettres apparait alors comme une application linéaire de E dans F. Elle se décrit par une matrice. Même si le corps est inhabituel, tous les résultats de l'algèbre linéaire s'appliquent ici. Pour cette raison, un tel code est dit linéaire. L'encodage consiste à multiplier le vecteur de quatre lettres binaires par une matrice 7x4 pour obtenir un vecteur composé de sept lettres binaires.
Matrice génératrice
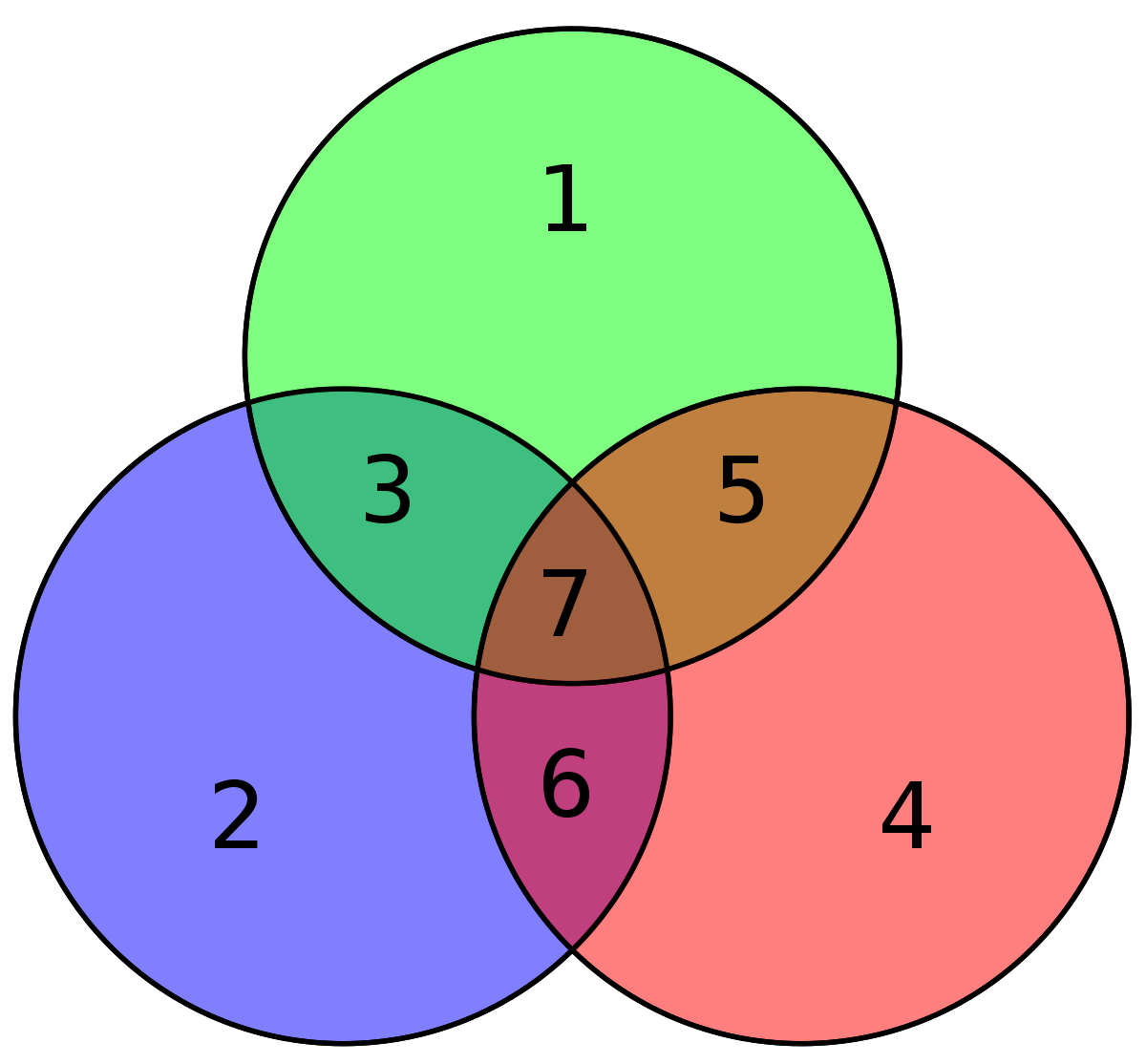
La connaissance de l'image de chaque vecteur de la base canonique détermine entièrement l'application d'encodage φ. Les quatre vecteurs de la base correspondent aux messages suivants : d1 = 1000, d2 = 0100, d3 = 0010 et d4 = 0001.
L'image de d1, le message qui a des coordonnées nulles en d2, d3 et d4, possède deux parités égales à un, celle de p1 et p2 et une égale à zéro:p3.
En respectant l'ordre de la base de F : p1, p2, d1, p3, d2, d3 et d4, on obtient l'image du premier vecteur :
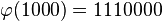
Calculons de la même manière les images des autres vecteurs de la base de E :
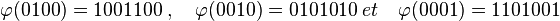
La matrice de φ, appelée matrice génératrice est formée des quatre colonnes correspondant aux images des vecteurs de la base canonique par φ, on obtient :
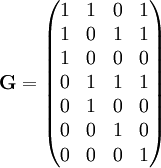
Exemple
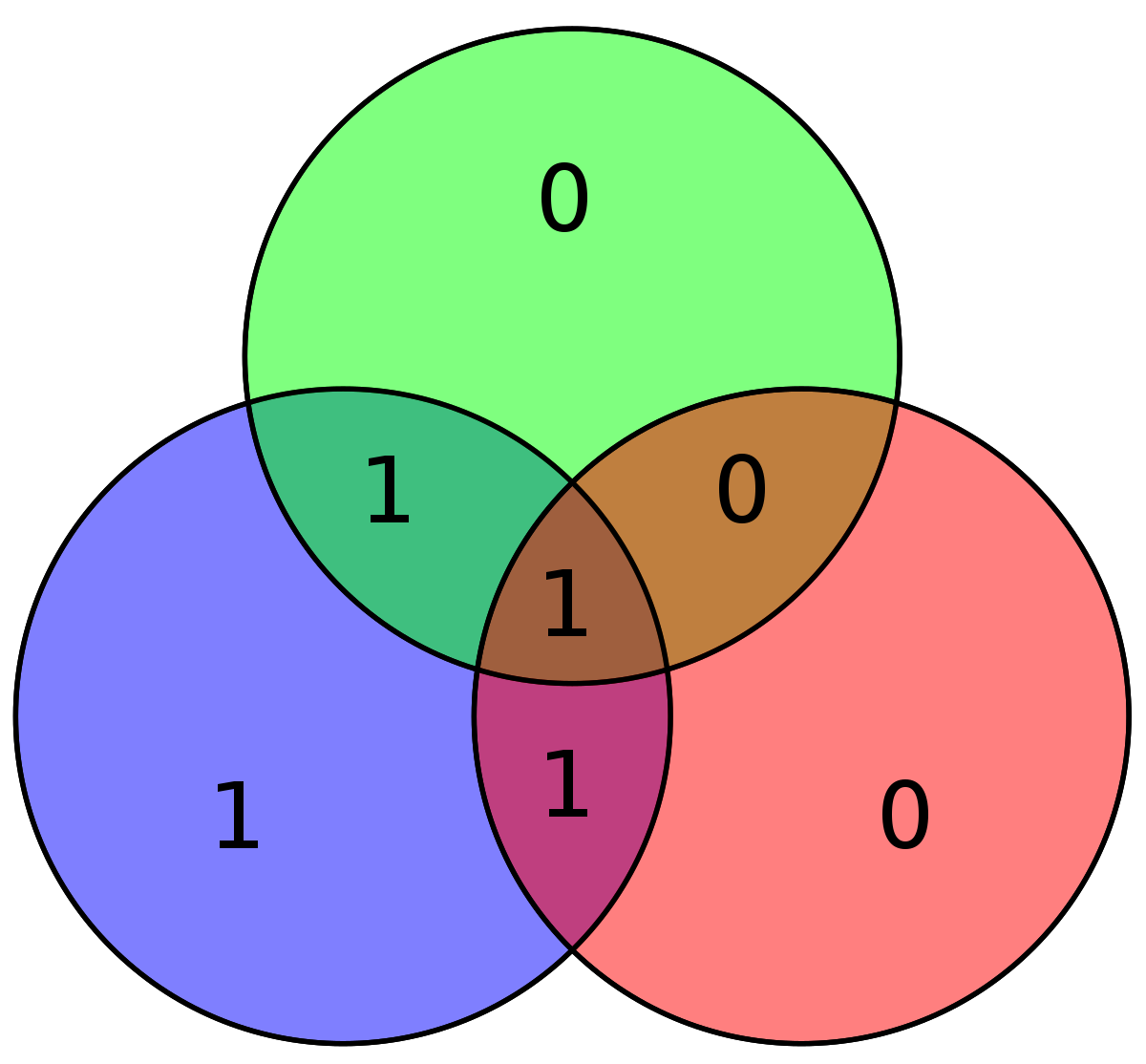
Considérons l'exemple du message à communiquer d = 1011. Les bits de parités sont alors égaux à zéro pour p1, un pour p2 et zéro pour p3. En respectant l'ordre des vecteurs de la base de F, on obtient manuellement le vecteur c = 0110011. Le produit matriciel de la matrice génératrice G par la matrice colonne D du vecteur d fournit la matrice colonne C du vecteur c:
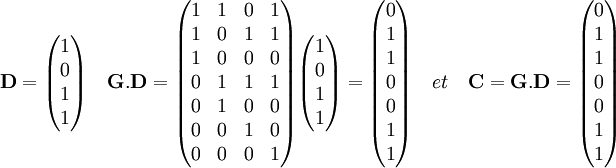
Les deux résultats sont égaux, cependant le calcul matriciel est simple et rapide à implémenter. Le destinataire reçoit le code c contenant à la fois des données et les bits de parité.
Code de Hamming (8,4)
En cas d'une double erreur, le code détecte une anomalie. Cependant le syndrome propose un chiffre binaire correspondant toujours à une troisième colonne différente des deux précédentes. Ainsi une troisième erreur est ajoutée, car le code ne dispose d'aucun moyen pour différencier une simple d'une double erreur. Pour pallier cet état de fait, ainsi que pour obtenir un code de dimension exactement égale à un octet, un huitième bit est souvent ajouté, il correspond à la parité des sept bits précédents. Une deuxième erreur est ainsi détectée, elle ne peut être corrigée, en revanche l'information d'une double erreur est disponible remplaçant une tentative maladroite, par une demande de retransmission.
Le décodage se fait de la manière suivante :
- S’il n’y a aucune erreur le syndrome est nul.
- Si une erreur s’est produite sur les sept premiers bits, les trois premiers éléments du syndrome donnent la position de l'erreur. L'existence d'un nombre d'erreur impair est confirmé par le huitième bit.
- Si deux erreurs se sont produites, les trois premiers éléments du syndrome ne sont pas tous nuls et le huitième bit indique une parité exact, signal d'un nombre pair d'erreurs. Une retransmission est nécessaire.
- Si une erreur s'est produite sur le huitième bit, l'absence d'erreur sur les trois premiers éléments du syndrome permet de localiser l'erreur et le message est validé.
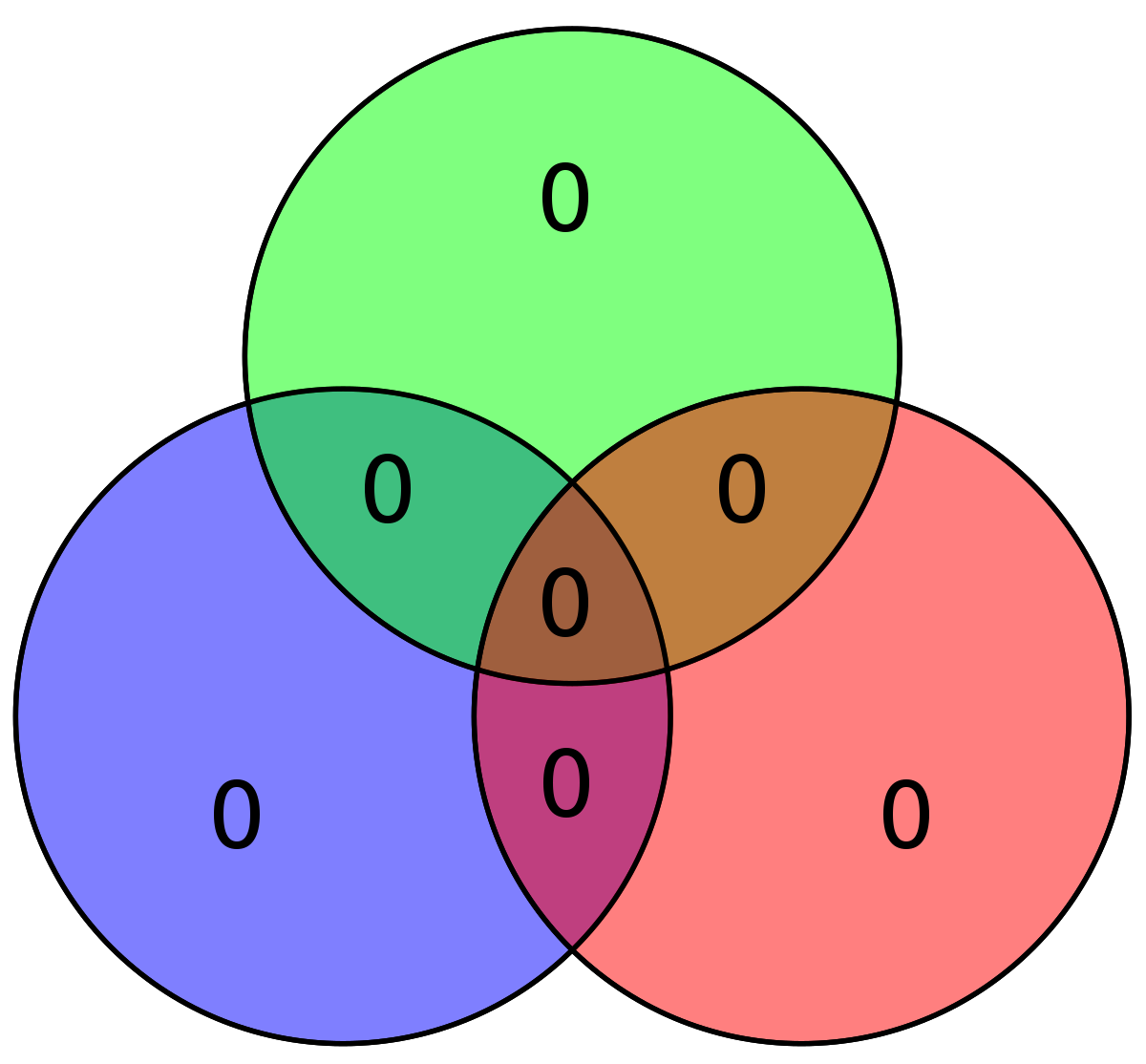
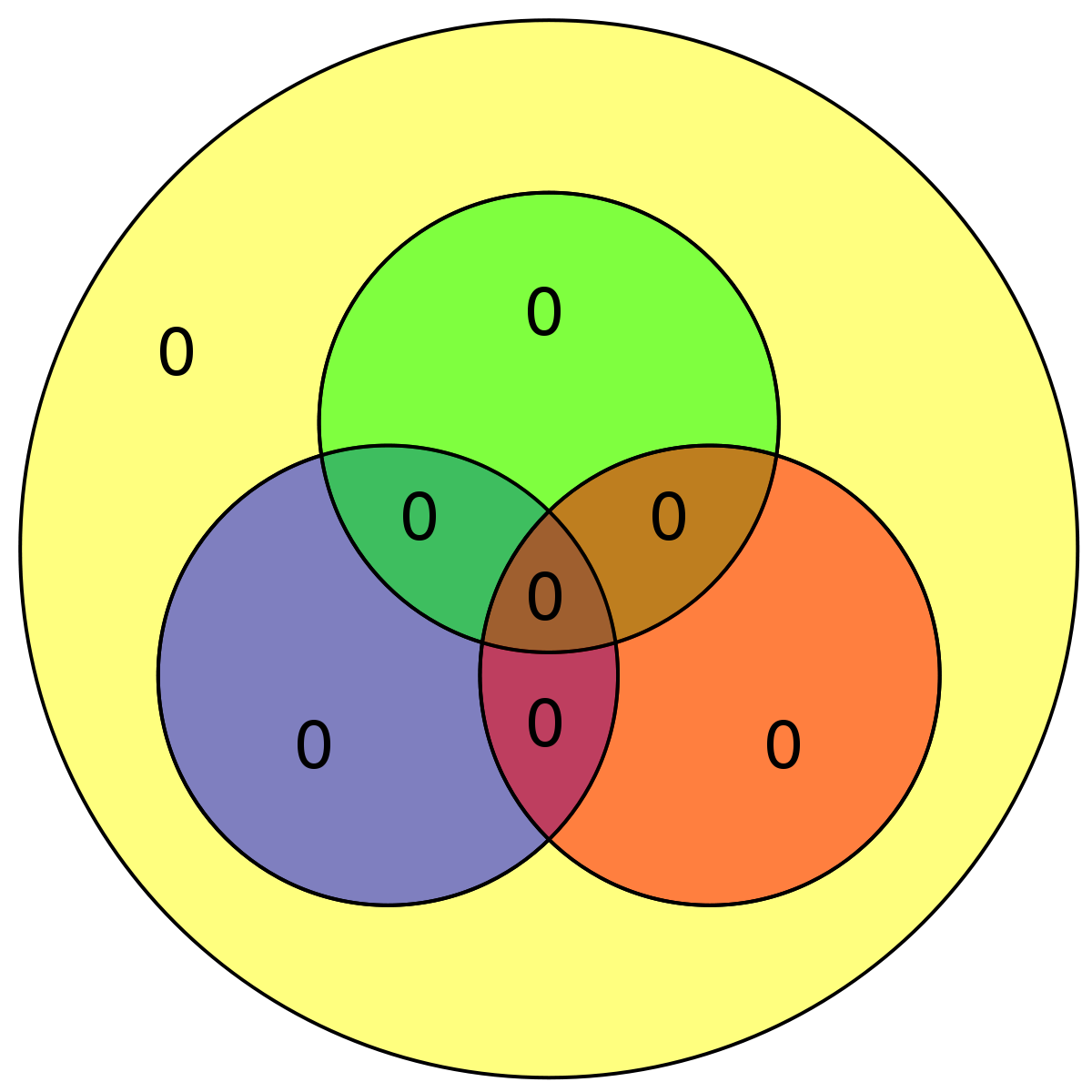
Le tableau suivant décrit les quatre premiers messages ainsi que leurs encodages pour Hamming (7,4) et (8,4)
| Données | Hamming(7,4) | Hamming(7,4) avec bit de parité (Hamming(8,4)) | ||
|---|---|---|---|---|
| Transmis | Diagramme | Transmis | Diagramme | |
| 0000 | 0000000 |
| 00000000 |
|
| 1000 | 1110000 |
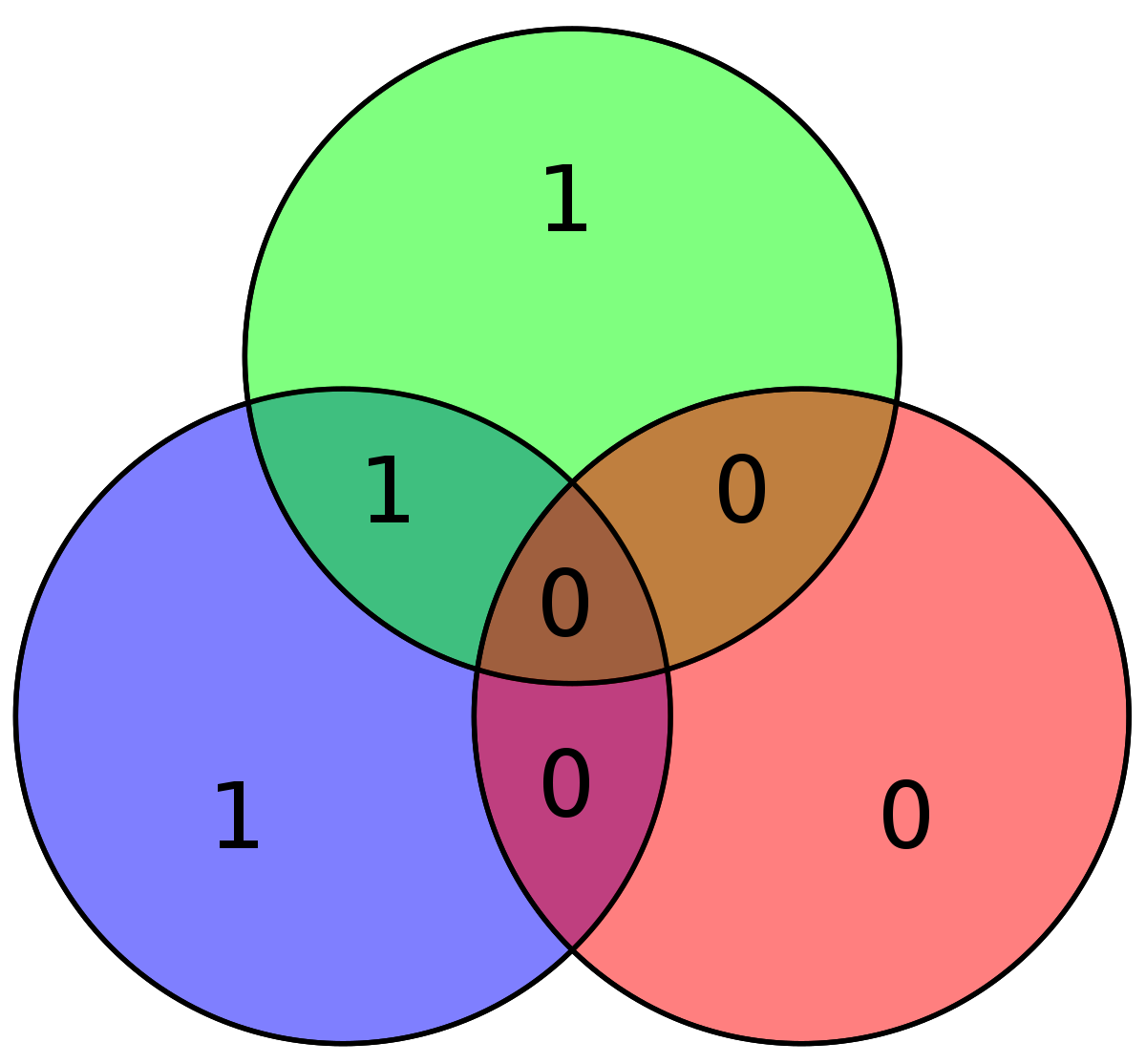
| 11100001 |
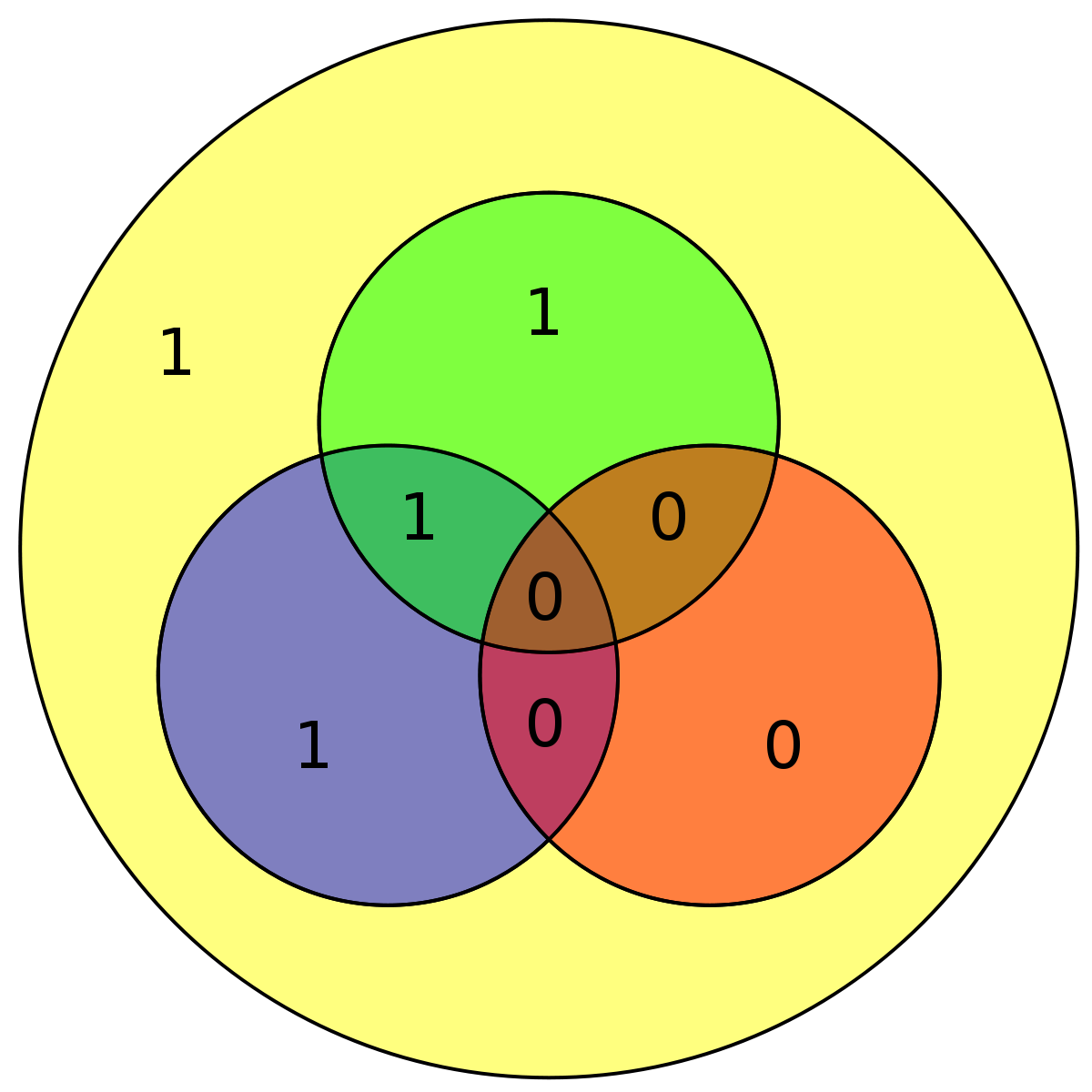
|
| 0100 | 1001100 |
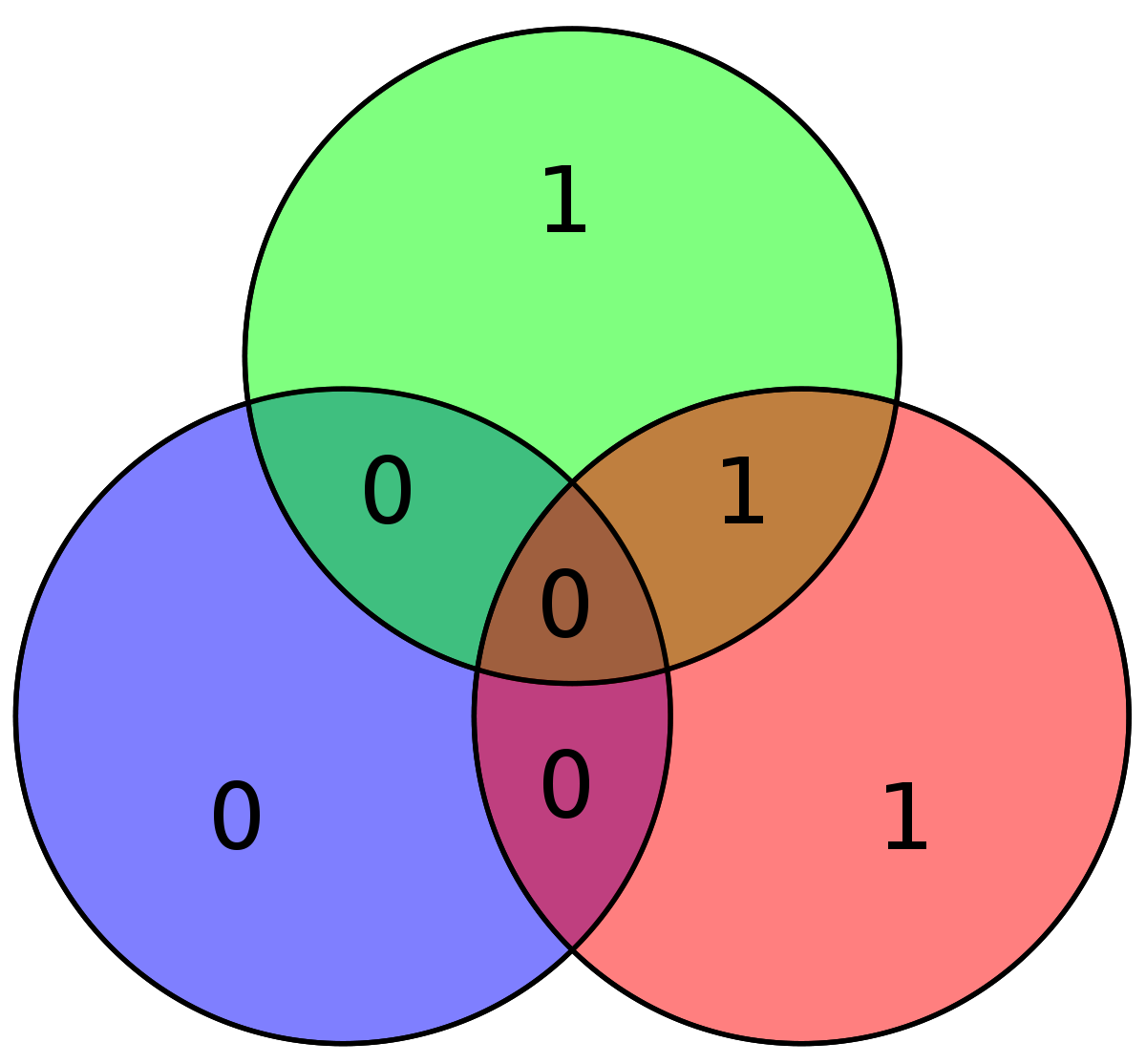
| 10011001 |
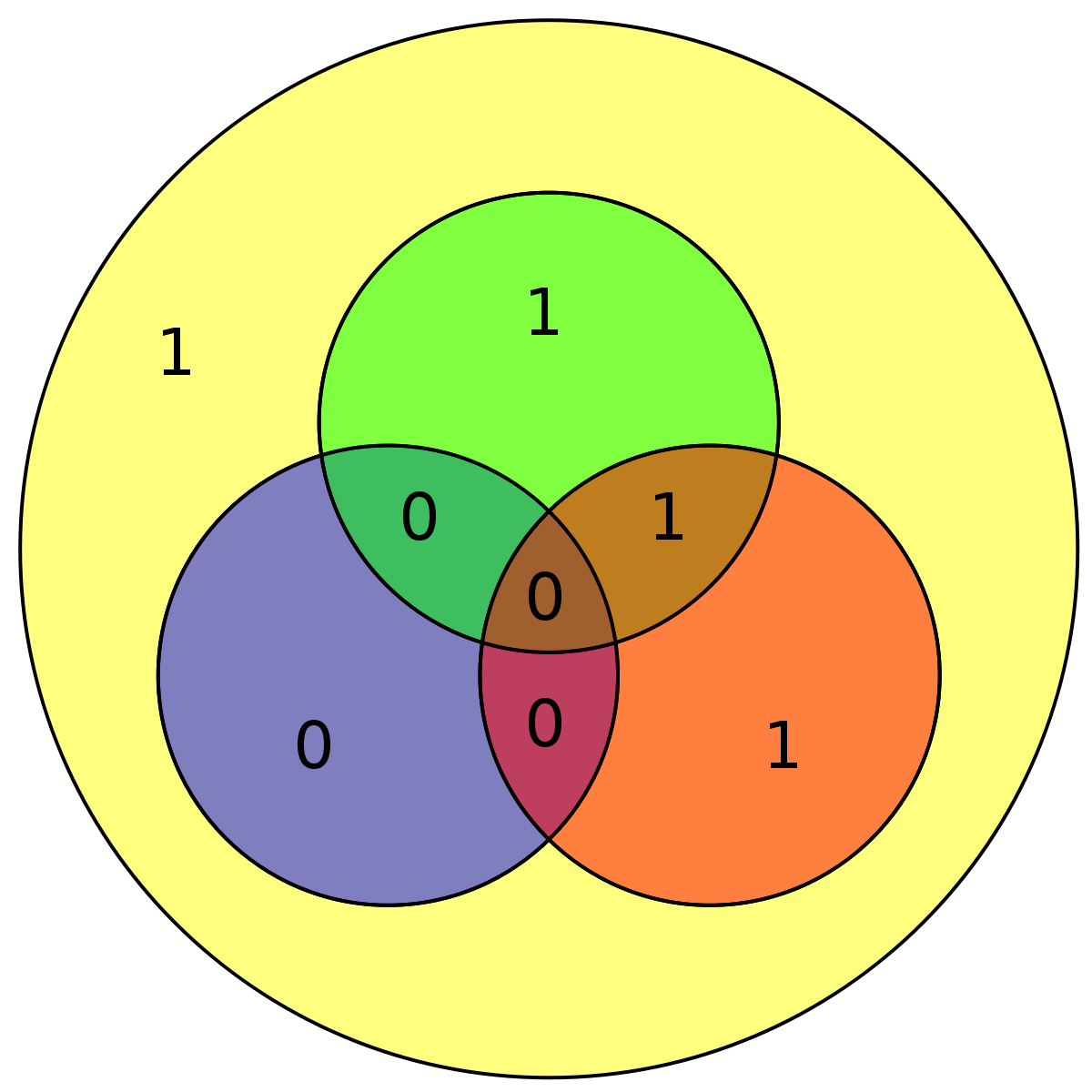
|
| 1100 | 0111100 |
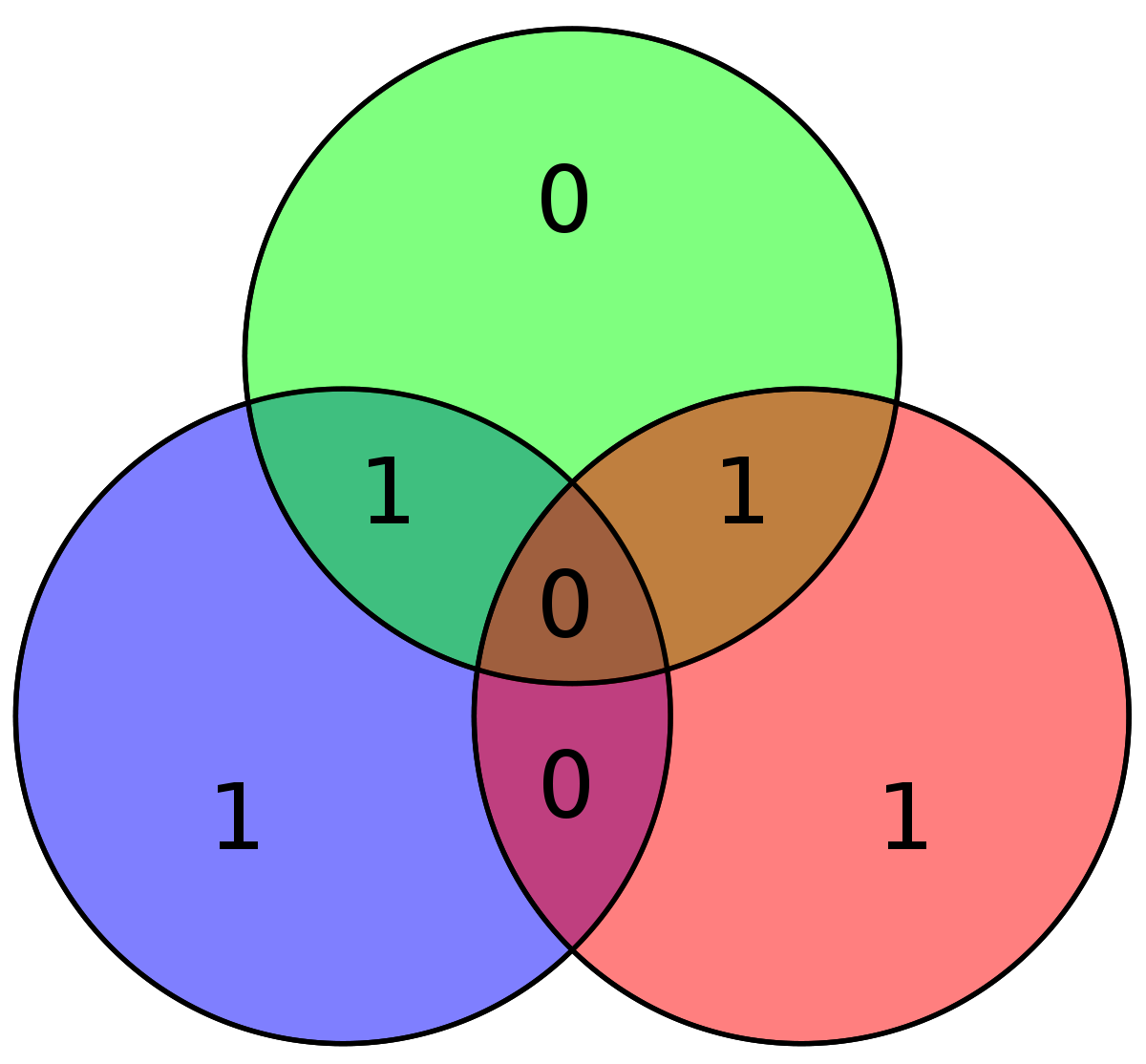
| 01111000 |
|