Codage entropique - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Définitions - Inégalité de Kraft - Propriétés des codes de source - Code optimal - Applications - Types de codes

Introduction

Le codage entropique (ou codage statistique à longueur variable) est une méthode de codage de source sans pertes, dont le but est de transformer la représentation d'une source de données pour sa compression et/ou sa transmission sur un canal de communication. Les principaux types de codage entropique sont le codage de Huffman et le codage arithmétique.

Le codage entropique utilise des statistiques sur la source pour construire un code, c'est-à-dire une application qui associe à une partie de la source un mot de code, dont la longueur dépend des propriétés statistiques de la source. On utilise donc en général un code à longueur variable, qui affecte les mots de codes les plus courts aux symboles de source les plus fréquents. Le codage entropique est issu de la théorie de l'information, et traite de ces codes et de leurs propriétés. L'information à coder est représentée par une variable aléatoire à valeur dans un alphabet de taille finie. Un résultat important est le théorème du codage de source, qui établit la limite à la possibilité de compression, et établit cette limite comme étant l'entropie.

Historiquement développé dans les années 1940-50 avec la théorie de l'information, le codage entropique est devenu une technique fondamentale en compression de données, et est présent dans de nombreux programmes de compression et de normes de compression d'image et de compression vidéo.

Définitions

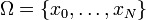
On considère une source discrète, c'est-à-dire un dispositif qui fournit aléatoirement des séquences de symboles issus d'un ensemble discret fini. Une source peut être un texte, une image, ou plus généralement, tout signal numérique. Une source est modélisée par un ensemble de variables aléatoires, à valeur dans un alphabet de taille finie, $\Omega=\{x_0, \ldots,x_N\}$ . $Ω$ est appelé l'ensemble des symboles de source.

Définition — Une source est dite sans mémoire si la séquence de symboles générée par la source est une suite de variables indépendantes et identiquement distribuées.

Définition — Un code de source C pour une variable aléatoire $X$ de distribution de probabilité $p$ , est une application de $Ω$ vers l'ensemble des chaînes de symboles d'un alphabet D-aire $A$ .

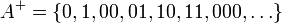
L'ensemble des chaînes de symboles d'un alphabet D-aire $A$ est noté $A +$ . En général, cet alphabet est binaire et on a $D = 2$ , $A = {0,1}$ . $A +$ est alors l'ensemble des chaînes de caractères de taille finie formées de 0 et de 1, $A^+=\{0, 1, 00, 01, 10, 11, 000, \ldots\}$ . Un code associe à un symbole de source $x$ un mot de code $C (x)$ . Ce mot de code est de longueur variable $l (x)$ , la longueur étant son nombre de bits. Ces codes sont appelés codes à longueur variable.

L'espérance de la longueur d'un code $C$ (ou longueur moyenne, selon la loi de probabilité de X) est donnée par:

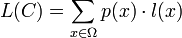
$L (C)$ peut également se voir comme le taux de codage, c'est-à-dire le nombre moyen de bits codés par symbole de source.

Définition — L'extension $C +$ d'un code $C$ est l'application de $Ω +$ dans $A +$ , qui associe à une séquence de symboles de source la concaténation de ses mots de code:

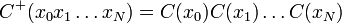
Cette définition est motivée par le fait que l'on transmet des séquences de symboles, et non des symboles isolés séparés par un symbole de séparation, ce qui serait inefficace.

Inégalité de Kraft

L'inégalité de Kraft donne une condition nécessaire et suffisante sur les longueurs des mots de code pour qu'un code soit préfixé. Pour un code défini sur un alphabet de taille $D$ , et un alphabet de source $Ω$ de taille $| Ω |$ , alors il est préfixé si et seulement si $\sum_{i=1}^{|\Omega|} D^{-l_i} \leq 1.$