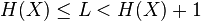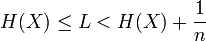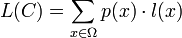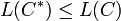Codage de Huffman - Définition

Limitations du codage de Huffman

On peut montrer que pour une source X, d'entropie H(X) la longueur moyenne L d'un mot de code obtenu par codage de Huffman vérifie:

Cette relation, qui montre que le codage de Huffman s'approche effectivement de l'entropie de la source et donc de l'optimum, peut s'avérer en fait assez peu intéressante dans le cas où l'entropie de la source est faible, et où un surcoût de 1 bit devient important. De plus le codage de Huffman impose d'utiliser un nombre entier de bit pour un symbole source, ce qui peut s'avérer peu efficace.

Une solution à ce problème est de travailler sur des blocs de n symboles. On montre alors qu' on peut s'approcher de façon plus fine de l'entropie:

mais le processus d'estimation des probabilités devient plus complexe et coûteux.

De plus, le codage de Huffman n'est pas adapté dans le cas d'une source dont les propriétés statistiques évoluent au cours du temps, puisque les probabilités des symboles sont alors erronées. La solution consistant à ré-estimer à chaque itération les probabilités symboles est impraticable du fait de sa complexité. La technique devient alors le codage Huffman adaptatif : à chaque nouveau symbole la table des fréquences est remise à jour et l'arbre de codage modifié si nécessaire. Le décompresseur faisant de même pour les mêmes causes … il reste synchronisé sur ce qu'avait fait le compresseur.

En pratique, lorsque l'on veut s'approcher de l'entropie, on préfèrera un codage arithmétique qui est optimal au niveau du bit.

Propriétés

Un code de Huffman est un code de source. Pour une source S, représentée par une variable aléatoire X, de distribution de probabilité p, l'espérance de la longueur d'un code C est donnée par

Où l(x) est la longueur du mot de code C(x), le code associé au symbole de source x, et Ω est l'ensemble des symboles de source.

Un code de Huffman est un code préfixe à longueur variable. Il est optimal, au sens de la plus courte longueur, pour un codage par symbole. C'est-à-dire que pour un code de Huffman C ^* , et pour tout code C uniquement décodable, alors:

Anecdote

Les premiers Macintosh de la société Apple utilisaient un code inspiré de Huffman pour la représentation des textes : les 15 caractères les plus fréquents d'une langue étaient codés sur 4 bits, et la 16ème configuration servait de préfixe au codage des autres sur un octet (ce qui faisait donc tantôt 4 bits, tantôt 12 bits par caractère). Cette méthode simple se révélait économiser 30% d'espace sur un texte moyen, à une époque où la mémoire vive restait encore un composant coûteux.

Utilisations

Le codage de Huffman ne se base que sur la fréquence relative des symboles d'entrée (suites de bits) sans distinction pour leur provenance (images, vidéos, sons, etc.). C'est pourquoi il est en général utilisé au second étage de compression, une fois la redondance propre au média mise en évidence par d'autres algorithmes. On pense en particulier à la compression JPEG pour les images, MPEG pour les vidéos et MP3 pour le son, qui peuvent retirer les éléments superflus imperceptibles pour les humains. On parle alors de compression avec perte.

D'autres algorithmes de compression, dits sans perte, tels que ceux utilisés pour la compression de fichiers, utilisent également Huffman pour comprimer le dictionnaire résultant. Par exemple, LZH (Lha) et deflate (ZIP, gzip) combinent un algorithme de compression par dictionnaire (dit de Lempel-Ziv) et un codage entropique de Huffman.