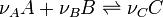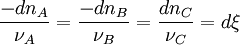Cinétique chimique - Définition

Vitesse de réaction

Considérons une réaction dont l'équation bilan s'écrit :

, et sont les coefficients stœchiométriques qui sont généralement des entiers naturels.

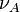
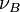
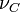
Lorsque la réaction progresse, les réactifs de départ disparaissent alors que les produits se forment en respectant la stœchiométrie de la réaction, c'est-à-dire les proportions indiquées par les coefficients de l'équation bilan.

Si à la date t, la progression de la réaction se traduit par une variation des quantités  ;  ; le respect de la stœchiométrie permet d'écrire que tous les rapports sont égaux au signe près.

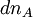
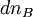
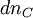
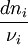
Ce rapport défini la variation de l'avancement de la réaction (noté ) entre son état initial (avancement nul) et son l'état final (avancement maximal).

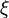
La vitesse molaire de réaction est définie par la dérivée de l'avancement de la réaction par rapport au temps: . Elle s'exprime donc en mole par unité de temps. (Nota : on utilise souvent à la place de ).

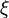
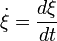
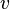
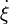
Dans le cas fréquent de réactions s'effectuant dans un système de volume constant (c'est en particulier les cas des réactions en solution), la vitesse est définie par rapport à la variation de la concentration. On l'appelle alors vitesse spécifique ou globale volumique de réaction : .

• est la concentration de l'espèce
• est son coefficient stœchiométrique. Dans cette relation (tout comme dans la définition de l'avancement de réaction) est affecté du signe - pour les réactifs et du signe + pour les produits qui se forment.

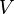
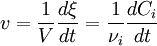
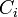
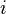
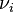
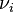
Dans les unités du SI, la vitesse volumique s'exprime en mol.m⁻³.s⁻¹ ou en mol.L⁻¹.s⁻¹.

Pour les réactions en phases gazeuse, on peut définir la vitesse par rapport à la dérivée de la pression partielle .

étant la pression partielle du constituant . Dans les unités du SI, elle s'exprime en Pa.s^-1.

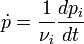
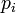
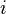
Loi de vitesse et Ordre de réaction

On appelle loi de vitesse la relation qui existe entre la vitesse et tous les facteurs qui ont une influence sur celle-ci.

Parmi ces facteurs, on distingue d'une part les facteurs physiques (et en particulier la température) et, d'autre part, les quantités (ou les concentrations) des substances présentes dans le milieu réactionnel (et en particulier les réactifs).

La loi de vitesse peut se mettre sous la forme d'un produit de deux fonctions : . Le premier facteur est le coefficient de vitesse (ou constante de vitesse) qui dépend notamment de la température, le second est une fonction des quantités (ou des concentrations) des substances présentes dans le milieu réactionnel.

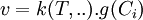
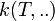
La loi de vitesse doit être établie expérimentalement à partir de séries d'expériences judicieusement conçues en faisant varier les différents facteurs

Dans certains cas, la fonction peut se mettre sous la forme d'un monôme : . On dit alors que la réaction admet un ordre et l'on appelle ordre de réaction la somme des exposants : . L'exposant est l'ordre partiel de la réaction par rapport à l'espèce .

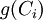
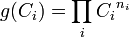
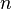
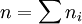
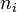
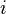
À noter que les ordres partiels ne sont pas nécessairement égaux aux coefficients stœchiométriques, ils ne sont même pas nécessairement entiers ni positifs, ce peut être des nombres fractionnaires et même des nombres réels.

Si la loi de vitesse ne peut pas se mettre sous la forme d'un monôme avec les concentrations comme facteurs, on dit que la réaction n'admet pas d'ordre.

Cas de l'activation thermique

La température est le facteur ayant la plus grande influence sur la vitesse des réactions chimiques. Dans un très grand nombre de cas la vitesse de la réaction augmente d'un facteur 2 à 3 lorsque la température augmente de 10 degrés. La dépendance de la vitesse de réaction en fonction de la température a fait l'objet d'études expérimentales intensives à la fin du XIX^e siècle. Plusieurs équations empiriques ont alors été proposées, mais c'est la Loi d'Arrhenius qui s'est imposée au début du XX^e siècle. Cette loi a été vérifiée depuis pour un très grand nombre de réactions.

Selon la loi d'Arrhénius, la température intervient dans un facteur exponentiel dans lequel est appelé « énergie d'activation d'Arrhénius », R la constante des gaz parfaits, T la température en kelvin, K la constante de vitesse de la réaction et A un facteur pré-exponentiel dépendant de la réaction.

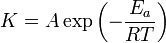
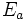
Outre son importance pratique, la loi d'Arrhenius a une grande importance théorique car elle est compatible avec la théorie des collisions qui permet de jeter un pont entre la représentation microscopique (à l'échelle des molécules) de la réaction chimique et l'observation macroscopique de sa vitesse.

Toutes les réactions ne suivent pas la loi d'Arrhénius. C'est en particulier le cas des réactions explosives, des réactions catalysées par les enzymes ou ayant d'autres modes d'activation que l'activation purement thermique (activation par rayonnement, par électrochimie ou par micro-ondes).

Par exemple, pour la réaction suivante : 2 HCl (aq) + Mg(s) → H₂ (g) + MgCl₂ (aq), la vitesse de réaction augmente lorsqu'on baisse la température.