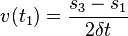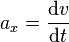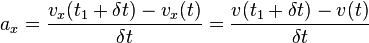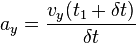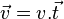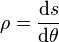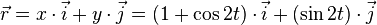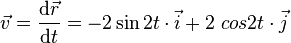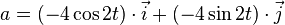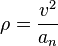Cinématique - Définition

Mouvement quelconque

Pour considérer les mouvement quelconques, on peut travailler de deux manières :

• considérer localement la tangente au mouvement, et utiliser les notions développées avec les trajectoires rectilignes uniformes
• considérer localement que l'on a un mouvement circulaire uniforme.

Ces deux approximations sont valables si l'on considère des temps courts.

Approximation tangentielle

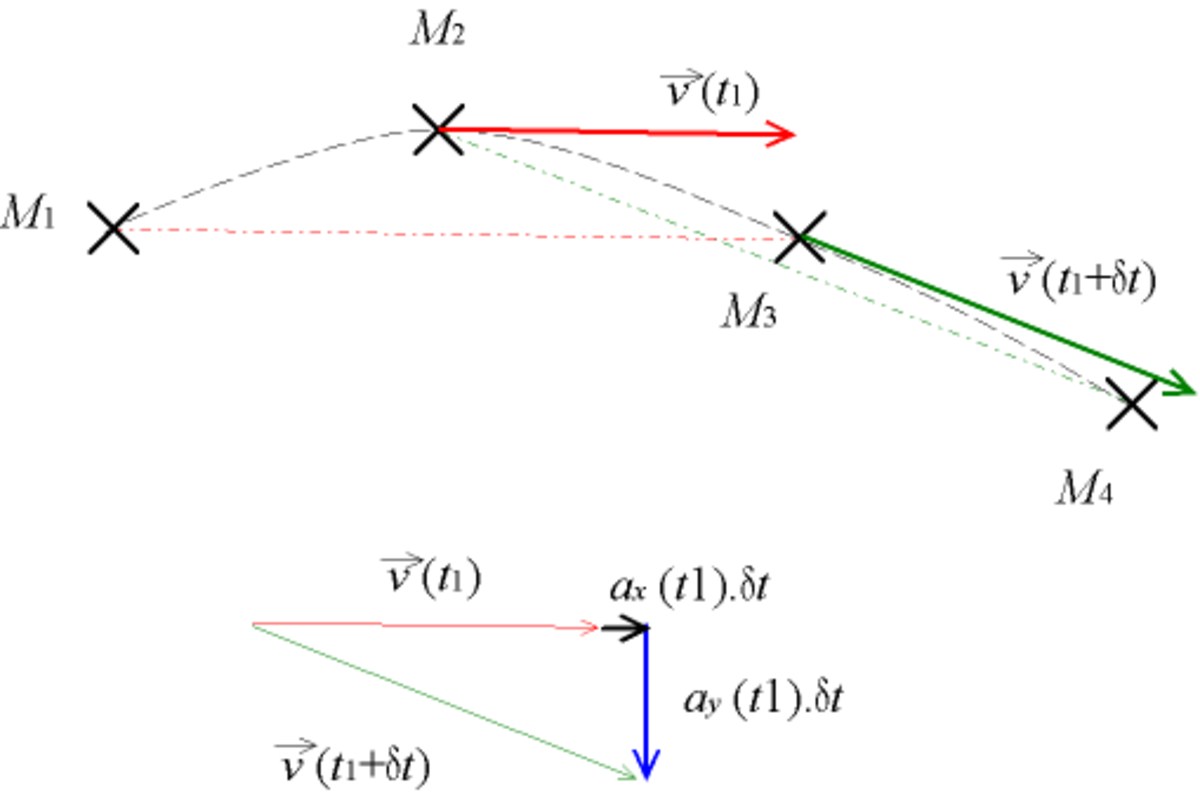
En général, le mouvement du centre d'inertie d'un mobile est enregistré de manière échantillonnée, c'est-à-dire que l'on a des points discrets correspondant à des position à des instants séparés d'une durée δt. Si l'on considère trois points consécutifs M₁, M₂ et M₃, correspondant à des instants t₁ − δt,t₁ et t₁ + δt.

La première approximation consiste à dire que la tangente en M₂ est parallèle à la corde [M₁M₃]. Ceci est légitimé par un théorème mathématique disant que pour une fonction continue et dérivable sur un intervalle, il existe un point de cet intervalle dont la dérivée vaut la pente entre les points extrêmes de la courbe sur cet intervalle (voir Théorème des accroissements finis). On peut aussi rapprocher cela du fait que sur un cercle, la médiatrice d'une corde passe par le milieu de la corde et est perpendiculaire à la tangente au milieu de la corde (puisque c'est un rayon).

La deuxième approximation consiste à estimer la norme de la vitesse constante entre M₁ et M₃, ce qui est acceptable si la durée est petite par rapport à l'accélération tangentielle. On estime donc que l'on a

La variation de ce vecteur vitesse donne le vecteur accélération. La composante tangentielle vaut :

ou par approximation

en effet, dans le repère de Frenet, on a v_x(t) = v(t), et on fait l'approximation v_x(t + δt) = v(t + δt) (approximation d'ordre 0). La composante normale est donnée par la variation de direction du vecteur vitesse ; on a v_y(t₁) = 0 par définition du repère de Frenet, soit

(approximation d'ordre 1, puisque l'ordre 0 est nul).

Dans le cas où le mouvement est lent par rapport à la précision de la mesure, la position enregistrée va avoir des variations dues aux incertitudes de mesure ; ainsi, au lieu d'avoir une courbe lisse, on va avoir une courbe présentant des oscillations (du bruit). Si l'on prend les points tels quels, on va calculer des vitesses instantanées incohérentes qui vont se répercuter sur les calculs des accélérations. Si les données sont traitées de manière informatique, on effectue donc un lissage des données.

Rayon de courbure

choisissons sur une courbe (C) un point M comme origine, et désignons par M(t) la position du mobile à l'instant t et par s = MM l'abscisse curviligne du point M.

On définit en tout point le rayon de courbure ρ de la trajectoire, par :

où dθ est l'angle formé entre les deux vecteurs vitesse aux points M(t) et M'(t+dt).

Exemple

Dans le repère , considérons le mouvement d'équation horaire :

x = 1 + cos 2t et y = sin 2t

le vecteur position s'écrit

le vecteur vitesse s'écrit

le module du vecteur vitesse est

, c'est une constante.

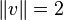
L'accélération tangentielle est

.

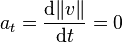
Le vecteur accélération totale est :

son module est

, c'est une constante.

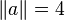
Les accélérations totale, tangentielle et normale forment un triangle rectangle ayant l'accélération totale pour hypoténuse ; alors d'après le théorème de Pythagore on a : a² = a² + a² ce qui donne que

a = 4

Or on a :

donc

ρ = 1, c'est une constante

donc cette courbe n'est autre qu'un cercle.