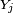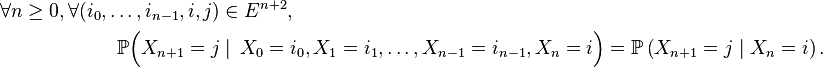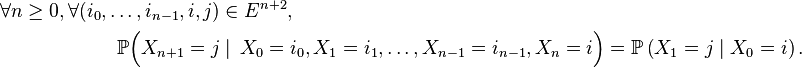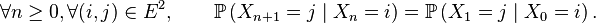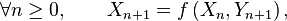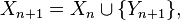Chaîne de Markov - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Selon les auteurs, une chaîne de Markov est de manière générale un processus de Markov à temps discret ou un processus de Markov à temps discret et à espace d'états discret. En mathématiques, un processus de Markov est un processus stochastique possédant la propriété de Markov : de manière simplifiée, la prédiction du futur, sachant le présent, n'est pas rendue plus précise par des éléments d'information supplémentaires concernant le passé. Les processus de Markov portent le nom de leur découvreur, Andreï Markov.
Un processus de Markov à temps discret est une séquence 
de variables aléatoires à valeurs dans l’espace des états, qu'on notera 
dans la suite. La valeur 
est l'état du processus à l'instant 
Les applications où l'espace d'états est fini ou dénombrable sont innombrables : on parle alors de chaîne de Markov ou de chaînes de Markov à espace d'états discret. Les propriétés essentielles des processus de Markov généraux, par exemple les propriétés de récurrence et d'ergodicité, s'énoncent ou se démontrent plus simplement dans le cas des chaînes de Markov à espace d'états discret. Cet article concerne précisément les chaînes de Markov à espace d'états discret.
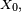
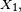
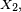
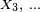
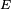
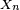
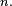
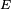
Andrei Markov a publié les premiers résultats sur les chaînes de Markov à espace d'états fini en 1906. Une généralisation à un espace d'états infini dénombrable a été publiée par Kolmogorov en 1936. Les processus de Markov sont liés au mouvement brownien et à l'hypothèse ergodique, deux sujets de physique statistique qui ont été très importants au début du XXe siècle.
Propriété de Markov faible
Définitions
C'est la propriété caractéristique d'une chaîne de Markov : la prédiction du futur à partir du présent n'est pas rendue plus précise par des éléments d'information supplémentaires concernant le passé, car toute l'information utile pour la prédiction du futur est contenue dans l'état présent du processus. La propriété de Markov faible possède plusieurs formes équivalentes qui reviennent toutes à constater que la loi conditionnelle de 
sachant le passé, i.e. sachant 
est une fonction de seul :
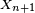
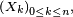
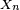
On suppose le plus souvent les chaînes de Markov homogènes, i.e. on suppose que le mécanisme de transition ne change pas au cours du temps. La propriété de Markov faible prend alors la forme suivante :
Cette forme de la propriété de Markov faible est plus forte que la forme précédente, et entraîne en particulier que
Dans la suite de l'article on ne considèrera que des chaînes de Markov homogènes. Pour une application intéressante des chaînes de Markov non homogènes à l'optimisation combinatoire, voir l'article Recuit simulé. Il existe une propriété de Markov forte, liée à la notion de temps d'arrêt : cette propriété de Markov forte est cruciale pour la démonstration de résultats importants (divers critères de récurrence, loi forte des grands nombres pour les chaînes de Markov). Elle est énoncée dans l'article "Propriété de Markov".
Critère
Critère fondamental — Soit une suite 
de variables aléatoires indépendantes et de même loi, à valeurs dans un espace 
, et soit 
une application mesurable de 
dans 
Supposons que la suite 
est définie par la relation de récurrence :
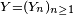
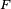
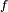
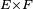
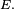
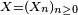
et supposons que la suite 
est indépendante de 
Alors 
est une chaîne de Markov homogène.
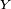
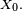
Petit Pierre fait la collection des portraits des onze joueurs de l'équipe nationale de football, qu'il trouve sur des vignettes à l'intérieur de l'emballage des tablettes de chocolat ; chaque fois qu'il achète une tablette il a une chance sur 11 de tomber sur le portrait du joueur n°
(pour tout ). On note ![\scriptstyle\ X_{n}\in\mathcal{P}([\![ 1,11]\!])\](https://static.techno-science.net/illustration/Definitions/autres/a/a724e9ac3370b700a53a33ea3da4024f_c5fc75e6f800b3960e6d04010d5167aa.png){kind=small}
l'état de la collection de Petit Pierre, après avoir ouvert l'emballage de sa 
-ème tablette de chocolat. est une chaîne de Markov partant de 
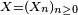
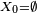
, car elle rentre dans le cadre précédent pour le choix ![\scriptstyle\ F=[\![1,11]\!],\ E=\mathcal{P}(F),\ f(x,y)=x\cup\{y\},\](https://static.techno-science.net/illustration/Definitions/autres/3/372498e85e6edf20771a7d7b8b861881_1c12d5c29698fb07cf9343eb733131fb.png){kind=small}
puisque
où les variables aléatoires 
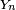
sont des variables aléatoires indépendantes et uniformes sur ![\scriptstyle\ [\![1,11]\!]\](https://static.techno-science.net/illustration/Definitions/autres/e/e76ea9e4de780d45f1e611b71c61ffb5_544a2def4e5601588348cdefb4b3b19f.png){kind=small}
: ce sont les numéros successifs des vignettes tirées des tablettes de chocolat. Le temps moyen nécessaire pour compléter la collection (ici le nombre de tablettes que Petit Pierre doit acheter en moyenne pour compléter sa collec') est, pour une collection de 
vignettes au total, de 
où 
est le -ème nombre harmonique. Par exemple, 
tablettes de chocolat.
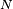
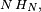
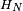
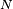
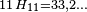
- La propriété de Markov découle de l'indépendance des
elle reste vraie lorsque les 
ont des lois différentes, et lorsque la "relation de récurrence" 
dépend de 
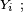
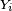
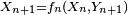
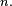
Les hypothèses faites en sus de l'indépendance sont là uniquement pour assurer l'homogénéité de la chaîne de Markov. - Le critère est fondamental en cela que toute chaîne de Markov homogène peut être simulée via une récurrence de la forme
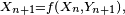
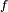
pour une fonction bien choisie. On peut même choisir ![\scriptstyle\ F=[0,1],\](https://static.techno-science.net/illustration/Definitions/autres/e/ec112d58275f3bfdad8c05658666a1cd_1ee3f81097be3b8694f003045c9f52df.png)
et choisir des variables 
indépendantes et uniformes sur l'intervalle [0,1], ce qui est commode pour l'étude de chaînes de Markov via des méthodes de Monte-Carlo.