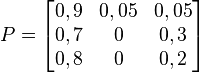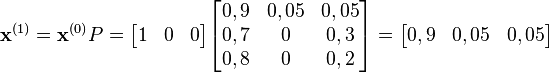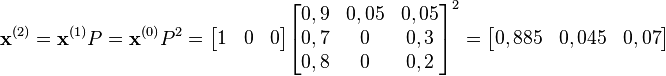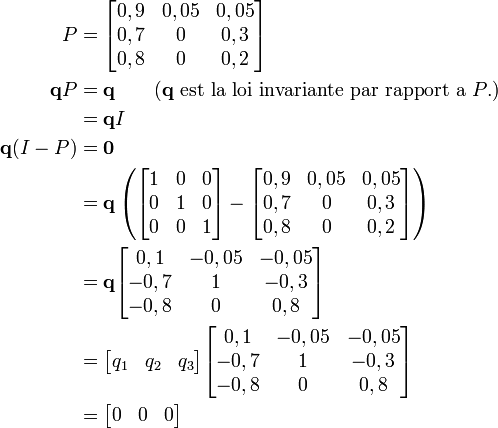Chaîne de Markov - Définition

Exemple : Doudou le hamster

Doudou, le hamster paresseux, ne connaît que trois endroits dans sa cage : les copeaux où il dort, la mangeoire où il mange et la roue où il fait de l'exercice. Ses journées sont assez semblables les unes aux autres, et son activité se représente aisément par une chaîne de Markov. Toutes les minutes, il peut soit changer d'activité, soit continuer celle qu'il était en train de faire. L'appellation processus sans mémoire n'est pas du tout exagérée pour parler de Doudou.

• Quand il dort, il a 9 chances sur 10 de ne pas se réveiller la minute suivante.
• Quand il se réveille, il y a 1 chance sur 2 qu'il aille manger et 1 chance sur 2 qu'il parte faire de l'exercice.
• Le repas ne dure qu'une minute, après il fait autre chose.
• Après avoir mangé, il y a 3 chances sur 10 qu'il parte courir dans sa roue, mais surtout 7 chances sur 10 qu'il retourne dormir.
• Courir est fatigant ; il y a 8 chances sur 10 qu'il retourne dormir au bout d'une minute. Sinon il continue en oubliant qu'il est déjà un peu fatigué.

Diagrammes

Les diagrammes peuvent montrer toutes les flèches, chacune représentant une probabilité de transition. Cependant, c'est plus lisible si :

• on ne dessine pas les flèches de probabilité zéro (transition impossible) ;
• on ne dessine pas les boucles (flèche d'un état vers lui-même). Cependant elles existent ; leur probabilité est sous-entendue car on sait que la somme des probabilités des flèches partant de chaque état doit être égale à 1.

exemple avec boucles implicites

exemple avec boucles dessinées

Matrice de transition

La matrice de transition de ce système est la suivante (les lignes et les colonnes correspondent dans l'ordre aux états représentés sur le graphe par copeaux, mangeoire, roue) :

Prévisions

Prenons l'hypothèse que Doudou dort lors de la première minute de l'étude.

Au bout d'une minute, on peut prédire :

Ainsi, après une minute, on a 90 % de chances que Doudou dorme encore, 5 % qu'il mange et 5 % qu'il coure.

Après 2 minutes, il y a 4,5 % de chances que le hamster mange.

De manière générale, pour n minutes :

La théorie montre qu'au bout d'un certain temps, la loi de probabilité est indépendante de la loi initiale. Notons la q :

On obtient la convergence si et seulement si la chaîne est apériodique et irréductible. C'est le cas dans notre exemple, on peut donc écrire :

Sachant que q₁ + q₂ + q₃ = 1, on obtient :

Doudou passe 88,4 % de son temps à dormir !

Applications

• Les systèmes Markoviens sont très présents en physique particulièrement en physique statistique. Plus généralement l'hypothèse markovienne est souvent invoquée lorsque des probabilités sont utilisées pour modéliser l'état d'un système, en supposant toutefois que l'état futur du système peut être déduit du passé avec un historique assez faible.

• Le célèbre article de 1948 de Claude Shannon, A mathematical theory of communication, qui fonde la théorie de l'information, commence en introduisant la notion d'entropie à partir d'une modélisation Markovienne de la langue anglaise. Il montre ainsi le degré de prédictibilité de la langue anglaise, muni d'un simple modèle d'ordre 1. Bien que simples, de tels modèles permettent de bien représenter les propriétés statistiques des systèmes et de réaliser des prédictions efficaces sans décrire la structure complète des systèmes.

• En compression, la modélisation markovienne permet la réalisation de techniques de codage entropique très efficaces, comme le codage arithmétique. De très nombreux algorithmes en reconnaissance des formes ou en intelligence artificielle comme par exemple l'algorithme de Viterbi, utilisé dans la grande majorité des systèmes de téléphonie mobile pour la correction d'erreurs, font l'hypothèse d'un processus markovien sous-jacent.

• L'indice de popularité d'une page Web (PageRank) tel qu'il est utilisé par Google est défini par une chaîne de Markov. Il est défini par la probabilité d'être dans cette page à partir d'un état quelconque de la chaine de Markov représentant le Web. Si N est le nombre de pages Web connues, et une page i a k_i liens, alors sa probabilité de transition vers une page liée (vers laquelle elle pointe) es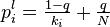t et 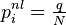pour toutes les autres (pages non liées). Notons qu'on a bien 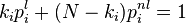. Le paramètre q vaut environ 0,15.

• Les chaînes de Markov sont un outil fondamental pour modéliser les processus en théorie des files d'attente et en statistiques.

• Les chaînes de Markov fondent les systèmes de Bonus/Malus mis au point par les actuaires des sociétés d'assurances automobiles (la probabilité d'avoir n accidents au cours de l'année t étant conditionnée par le nombre d'accidents en t-1)

• Les chaînes de Markov sont également utilisées en bioinformatique pour modéliser les relations entre symboles successifs d'une même séquence (de nucléotides par exemple), en allant au-delà du modèle polynomial. Les modèles markoviens cachés ont également diverses utilisations, telles que la segmentation (définition de frontières de régions au sein de séquences de gènes ou de protéines dont les propriétés chimiques varient), l'alignement multiple, la prédiction de fonction, ou la découverte de gènes (les modèles markoviens cachés sont plus « flexibles » que les définitions strictes de type codon start + multiples codons + codons stop et ils sont donc plus adaptés pour les eucaryotes (à cause de la présence d'introns dans le génome de ceux-ci) ou pour la découverte de pseudo-gènes).