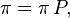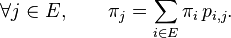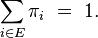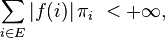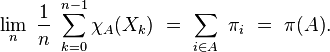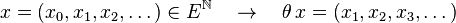Chaîne de Markov - Définition
La liste des auteurs de cet article est disponible ici.
Notation
Dans les formules qui précèdent, l'élément (i, j) est la probabilité de la transition de i à j. La somme des éléments d'une ligne vaut toujours 1 et la distribution stationnaire est donnée par le vecteur propre gauche de la matrice de transition.
On rencontre parfois des matrices de transition dans lesquelles le terme (i,j) est la probabilité de transition de j vers i, auquel cas la matrice de transition est simplement la transposée de celle décrite ici. La somme des éléments d'une colonne vaut alors 1. De plus, la distribution stationnaire du système est alors donnée par le vecteur propre droit de la matrice de transition, au lieu du vecteur propre gauche.
Loi stationnaire
Définition
Il peut exister une ou plusieurs mesures
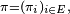
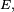
ou bien encore
Une telle mesure

Le terme « stationnaire » est justifié par la proposition suivante :
Proposition — Si la loi initiale de la chaîne de Markov (i.e. la loi de
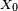
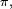
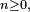
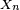
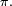
Cela découle des propriétés des donnée plus haut : la loi μn de Xn s'exprime en fonction de la loi μ0 de X0 de la manière suivante :
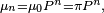
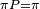
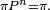
Plus généralement, la chaîne de Markov est un processus stationnaire si et seulement si sa loi initiale est une probabilité stationnaire.
Existence et unicité
Dans le cas des chaînes de Markov à espace d'états discret, certaines propriétés du processus déterminent s'il existe ou non une probabilité stationnaire, et si elle est unique ou non :
- une chaîne de Markov est irréductible si tout état est accessible à partir de n'importe quel autre état ;
- un état est récurrent positif si l'espérance du temps de premier retour en cet état, partant de cet état, est finie.
Si une chaîne de Markov possède au moins un état récurrent positif, alors il existe une probabilité stationnaire. S'il existe une probabilité stationnaire

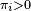 , alors l'état
, alors l'état

Théorème — Si une chaîne de Markov possède une seule classe finale
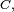
- il existe une unique probabilité stationnaire, notée
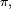
- il existe un état récurrent positif,
- tous les états de la classe finale sont récurrents positifs.
On a de plus l'équivalence
Ce théorème vaut en particulier pour les chaînes de Markov irréductibles, puisque ces dernières possèdent une seule classe (qui est donc nécessairement une classe finale) ; les chaînes de Markov irréductibles vérifient en particulier
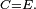
Loi forte des grands nombres et ergodicité
Dans le cas d'une chaîne de Markov irréductible et récurrente positive, la loi forte des grands nombres est en vigueur : la moyenne d'une fonction
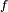
on a presque sûrement :
La moyenne de la valeur des instances est donc, sur le long terme, égale à l'espérance suivant la probabilité stationnaire. En particulier, cette équivalence sur les moyennes s'applique si
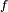
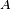
Cela permet d'approcher la probabilité stationnaire par la distribution empirique (qui est un histogramme construit à partir d'une séquence particulière), comme par exemple dans le cas de la marche aléatoire avec barrière.
En particulier, si le processus est construit en prenant la probabilité stationnaire comme loi initiale, le shift

préserve la mesure, ce qui fait de la chaîne de Markov un système dynamique. La loi forte des grands nombres entraine alors que la chaîne de Markov est un système dynamique ergodique. L'ergodicité est à la fois plus forte que la loi forte des grands nombres car on peut en déduire, par exemple, que
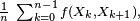
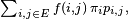
Convergence vers la loi stationnaire
Si la chaîne de Markov est irréductible, récurrente positive et apériodique, alors
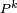
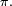
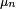
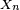

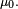
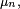
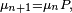
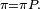
Chaînes de Markov à espace d'états fini
Si une chaîne de Markov est irréductible et si son espace d'états est fini, tous ses états sont récurrents positifs. La loi forte des grands nombres est alors en vigueur.
Plus généralement, tous les éléments d'une classe finale finie sont récurrents positifs, que l'espace d'états soit fini ou bien infini dénombrable.