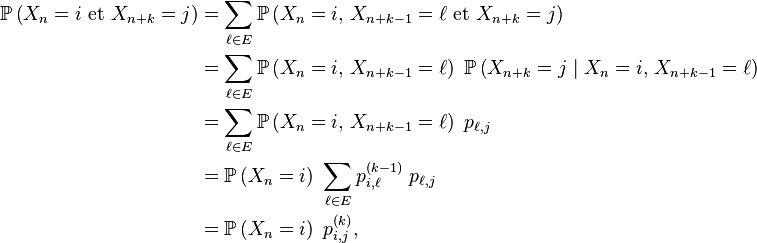Samedi 26 Avril 2025
Rechercher 🔍

Chaîne de Markov - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Propriété de Markov faible - Classification des états - Probabilités de transition - Notation - Loi stationnaire - Illustration de l'impact du modèle - Exemple : Doudou le hamster - Applications

Classification des états

Graphe de la marche du cavalier sur l'échiquier (quart Sud-Ouest de l'échiquier).

Pour \scriptstyle\ (i,j)\in E^2\ , on dit que \scriptstyle\ j\ est accessible à partir de \scriptstyle\ i\ si et seulement s'il existe \scriptstyle\ n\ge 0\ tel que \scriptstyle\ \mathbb{P}(X_{n}=j\mid X_0=i) >0.\ On note :

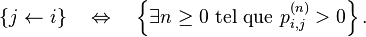
\{j\leftarrow i\}\quad\Leftrightarrow\quad\left\{\exists n\ge 0\text{ tel que }p^{(n)}_{i,j}>0\right\}.

On dit que \scriptstyle\ i\ et \scriptstyle\ j\ communiquent si et seulement s'il existe \scriptstyle\ (n,m)\in \mathbb{N}^2\ tels que \scriptstyle\ \mathbb{P}(X_{n}=j\mid X_0=i) >0\ et \scriptstyle\ \mathbb{P}(X_{m}=i\mid X_0=j) >0.\ On note :

\{j\leftrightarrow i\}\quad\Leftrightarrow\quad\left\{j\leftarrow i\text{ et }i\leftarrow j\right\}.

La relation communiquer, notée \scriptstyle\ \leftrightarrow,\ est une relation d'équivalence. Quand on parle de classe en parlant des états d'une chaîne de Markov, c'est général aux classes d'équivalence pour la relation \scriptstyle\ \leftrightarrow\ qu'on fait référence. Si tous les états communiquent, la chaîne de Markov est dite irréductible.

La relation être accessible, notée \scriptstyle\ \leftarrow,\ s'étend aux classes d'équivalence : pour deux classes \scriptstyle\ C\ et \scriptstyle\ C^{\prime}\ , on a

\{C\leftarrow C^{\prime}\}\quad\Leftrightarrow\quad\left\{\exists (i,j)\in C\times C^{\prime},\qquad i\leftarrow j\right\}\quad\Leftrightarrow\quad\left\{\forall (i,j)\in C\times C^{\prime},\qquad i\leftarrow j\right\}.

La relation \scriptstyle\ \leftarrow\ est une relation d'ordre entre les classes d'équivalence.


Une classe est dite finale si elle ne conduit à aucune autre, i.e. si la classe est minimale pour la relation \scriptstyle\ \leftarrow.\ Sinon, elle est dite transitoire. L'appartenance à une classe finale ou transitoire a des conséquences sur les propriétés probabilistes d'un état de la chaîne de Markov, en particulier sur son statut d'état récurrent ou d'état transient. Le nombre et la nature des classes finales dicte la structure de l'ensemble des probabilités stationnaires, qui résument de manière précise le comportement asymptotique de la chaîne de Markov, comme on peut le voir à la prochaine section et dans les deux exemples détaillés à la fin de cette page.

Soit

M_{ij} = \left\{n\ge 0\ |\ p^{(n)}_{i,j}>0\right\}.

La période d'un état \scriptstyle\ i\ est le PGCD de l'ensemble \scriptstyle\ M_{ii}.\ Si deux états communiquent, ils ont la même période : on peut donc parler de la période d'une classe d'états. Si la période vaut 1, la classe est dite apériodique. L'apériodicité des états d'une chaîne de Markov conditionne la convergence de la loi de \scriptstyle\ X_n\ vers la probabilité stationnaire, voir la page Probabilité stationnaire d'une chaîne de Markov.


La classification des états et leur période se lisent de manière simple sur le graphe de la chaîne de Markov. Toutefois, si tous les éléments de la matrice de transition sont strictement positifs, la chaîne de Markov est irréductible et apériodique : dessiner le graphe de la chaîne de Markov est alors superflu.

Probabilités de transition

Définition

Définition — Le nombre \scriptstyle\ \mathbb{P}\left(X_{1}=j\mid X_0=i\right) est appelé probabilité de transition de l'état \scriptstyle\ i\ à l'état \scriptstyle\ j\ en un pas, ou bien probabilité de transition de l'état \scriptstyle\ i\ à l'état \scriptstyle\ j, s'il n'y a pas d'ambiguité. On note souvent ce nombre \scriptstyle\ p_{i,j}:

p_{i,j} = \mathbb{P}\left(X_{1}=j\mid X_0=i\right).
  • La famille de nombres \scriptstyle\ P=\left(p_{i,j}\right)_{(i,j)\in E^2} est appelée matrice de transition, noyau de transition, ou opérateur de transition de la chaîne de Markov.

La terminologie matrice de transition est la plus utilisée, mais elle n'est appropriée, en toute rigueur, que lorsque, pour un entier \scriptstyle\ n\ge 1, \scriptstyle\ E=\{1,2,\ldots,n\}. Lorsque \scriptstyle\ E\ est fini, par exemple de cardinal \scriptstyle\ n, on peut toujours numéroter les éléments de \scriptstyle\ E\ arbitrairement de 1 à \scriptstyle\ n, ce qui règle le problème, mais imparfaitement, car cette renumérotation est contre-intuitive dans beaucoup d'exemples.

Modèle d'Ehrenfest : les deux chiens et leurs puces  :

Deux chiens se partagent \scriptstyle\ N\ puces de la manière suivante : à chaque instant, une des \scriptstyle\ N\ puces est choisie au hasard et saute alors d'un chien à l'autre. L'état du système est décrit par un élément \scriptstyle\ x=(x_1,x_2,\dots,x_N)\in\{0,1\}^N, où

x_{i} = 0\text{ ou }1\text{ selon que la puce n}^{\circ}\ i\text{ est sur le 1er ou sur le 2eme chien.}

Alors \scriptstyle\ E\ possède \scriptstyle\ 2^N\ éléments, mais les numéroter de 1 à \scriptstyle\ 2^N\ serait malcommode pour suivre l'évolution du système, qui consiste à choisir une des \scriptstyle\ N\ coordonnées de \scriptstyle\ x\ au hasard et à changer sa valeur. Si l'on veut comprendre le système moins en détail (car on n'est pas capable de reconnaître une puce d'une autre), on peut se contenter d'étudier le nombre de puces sur le chien n°1, ce qui revient à choisir \scriptstyle\ E=\{0, 1, 2,\dots, N\}. Là encore, pour la compréhension, il serait dommage de renuméroter les états de 1 à \scriptstyle\ N+1. Notons que pour cette nouvelle modélisation,

p_{k,k+1} = \tfrac{N-k}N\text{ et }p_{k,k-1} = \tfrac{k}N,

puisque, par exemple, le nombre de puces sur le dos du chien n°1 passe de k à k-1 si c'est une de ces k puces qui est choisie pour sauter, parmi les N puces présentes dans le "système". Ce modèle porte plus souvent le nom de "modèle des urnes d'Ehrenfest". Il a été introduit en 1907 par Tatiana et Paul Ehrenfest pour illustrer certains des « paradoxes » apparus dans les fondements de la mécanique statistique naissante, et pour modéliser le bruit rose. Le modèle des urnes d'Ehrenfest était considéré par le mathématicien Mark Kac [1] comme « ... probablement l'un des modèles les plus instructifs de toute la physique ... »

Plutôt que de renuméroter les états à partir de 1, il est donc plus ergonomique dans beaucoup de cas d'accepter des matrices finies ou infinies dont les lignes et colonnes sont "numérotées" à l'aide des éléments de \scriptstyle\ E. Le produit de deux telles "matrices", \scriptstyle\ A=\left(a_{i,j}\right)_{(i,j)\in E^2} et \scriptstyle\ B=\left(b_{i,j}\right)_{(i,j)\in E^2} , est alors défini très naturellement par

(AB)_{i,j} = \sum_{\ell\in E}a_{i,\ell}b_{\ell,j},

par analogie avec la formule plus classique du produit de deux matrices carrées de taille \scriptstyle\ n,

(AB)_{i,j} = \sum_{k=1}^na_{i,k}b_{k,j}.

Propriétés

Proposition — La matrice de transition \scriptstyle\ P=\left(p_{i,j}\right)_{(i,j)\in E^2}\ est stochastique : la somme des termes de n'importe quelle ligne de \scriptstyle\ P\ donne toujours 1.

\forall i\in E, \quad\sum_{j\in E}p_{i,j}=1.

Proposition —  La loi de la chaîne de Markov \scriptstyle\ X=\left(X_n\right)_{n\ge 0} est caractérisée par le couple constitué de sa matrice de transition \scriptstyle\ P, et de sa loi initiale (la loi de \scriptstyle\ X_0\ ) : pour tout \scriptstyle\ n\ge 1 la loi jointe de \scriptstyle\ (X_0,X_1,\ldots,X_n) est donnée par

\mathbb{P}\left(X_{0}=i_0,X_{1}=i_1,\ldots,X_{n-1}=i_{n-1},X_{n}=i_n\right)=\mathbb{P}\left(X_{0}=i_0\right)\ p_{i_{0},i_1}\,p_{i_{1},i_2}\,\ldots\,p_{i_{n-2},i_{n-1}}\,p_{i_{n-1},i_n}.

Par récurrence, au rang 0,

\mathbb{P}\left(X_{0}=i_0\right)=\mathbb{P}\left(X_{0}=i_0\right).

Au rang \scriptstyle\ n,\ en posant \scriptstyle\ P_k=\mathbb{P}\left(X_{0}=i_0,X_{1}=i_1,\ldots,X_{k-1}=i_{k-1},X_{k}=i_k\right),

\frac{P_n}{P_{n-1}}=\mathbb{P}\Big(X_{n}=i_n\mid\, X_0=i_0, X_1=i_1,\ldots, X_{n-1}=i_{n-1}\Big)=p_{i_{n-1},i_n},

en vertu de la propriété de Markov faible, donc si \scriptstyle\ P_{n-1}\ a l'expression attendue, alors \scriptstyle\ P_{n}\ aussi.

Lorsqu'on étudie une chaîne de Markov particulière, sa matrice de transition est en général bien définie et fixée tout au long de l'étude, mais la loi initiale peut changer lors de l'étude et les notations doivent refléter la loi initiale considérée sur le moment : si à un moment de l'étude on considère une chaîne de Markov de loi initiale définie par \scriptstyle\ \forall i\in E,\quad \mathbb{P}\left(X_{0}=i\right)=\mu_i,\quad alors les probabilités sont notées \scriptstyle\ \mathbb{P}_{\mu}\left(\dots\right),\quad et les espérances sont notées \scriptstyle\ \mathbb{E}_{\mu}\left[\dots\right].\quad En particulier, si \scriptstyle\ \mathbb{P}\left(X_{0}=j\right)=1,\quad on dit que la chaîne de Markov part de \scriptstyle\ j,\quad les probabilités sont notées \scriptstyle\ \mathbb{P}_{j}\left(\dots\right),\quad et les espérances sont notées \scriptstyle\ \mathbb{E}_{j}\left[\dots\right].\quad

Puissances de la matrice de transition

Pour \scriptstyle\ k\ge 1, la probabilité de transition en \scriptstyle\ k\ pas, \scriptstyle\ \mathbb{P}\left(X_{n+k}=j\mid X_n=i\right), ne dépend pas de \scriptstyle\ n  :

Proposition — La matrice de transition en \scriptstyle\ k\ pas, \scriptstyle\ \left(\mathbb{P}\left(X_{n+k}=j\mid X_n=i\right)\right)_{(i,j)\in E^2}, est égale à la puissance \scriptstyle\ k -ème de la matrice de transition \scriptstyle\ P. On note

p^{(k)}_{i,j}=\mathbb{P}\left(X_{n+k}=j\mid X_n=i\right),

et

P^k=\left(p^{(k)}_{i,j}\right)_{(i,j)\in E^2}.

Par récurrence. Au rang 1, c'est une conséquence de l'homogénéité de la chaîne de Markov déjà mentionnée à la section  :

\mathbb{P}\left(X_{n+1}=j\mid X_n=i\right) = \mathbb{P}\left(X_{1}=j\mid X_0=i\right).

Au rang \scriptstyle\ k,\

\begin{align}\mathbb{P}\left(X_n=i\text{ et }X_{n+k}=j\right)&= \sum_{\ell\in E}\mathbb{P}\left(X_n=i,\,X_{n+k-1}=\ell\text{ et }X_{n+k}=j\right) \\ &= \sum_{\ell\in E}\mathbb{P}\left(X_n=i,\,X_{n+k-1}=\ell\right)\ \mathbb{P}\left(X_{n+k}=j\mid X_n=i,\,X_{n+k-1}=\ell\right) \\ &= \sum_{\ell\in E}\mathbb{P}\left(X_n=i,\,X_{n+k-1}=\ell\right)\ p_{\ell,j} \\ &= \mathbb{P}\left(X_n=i\right)\ \sum_{\ell\in E}p^{(k-1)}_{i,\ell}\ p_{\ell,j} \\ &= \mathbb{P}\left(X_n=i\right)\ p^{(k)}_{i,j}, \end{align}

où

  • la 1-ère égalité est le troisième axiome des probabilités,
  • la 2-ème égalité est la définition d'une probabilité conditionnelle,
  • la 3-ème égalité est due à une forme de propriété de Markov faible,
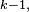
  • la 4-ème égalité est la propriété de récurrence au pas \scriptstyle\ k-1,
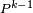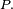
  • la 5-ème égalité est la formule du produit de deux "matrices", appliquée au produit de \scriptstyle\ P^{k-1} avec \scriptstyle\ P.

Pour conclure, on divise les deux termes extrêmes de cette suite d'égalités par \scriptstyle\ \mathbb{P}\left(X_n=i\right), sauf si ce dernier terme est nul, auquel cas on peut définir \scriptstyle\ \mathbb{P}\left(X_{n+k}=j\mid X_n=i\right)\ arbitrairement, donc, par exemple, égal à \scriptstyle\ p^{(k)}_{i,j}.

Par une simple application de la formule des probabilités totales, on en déduit les lois marginales de la chaîne de Markov.

Corollaire — La loi de \scriptstyle\ X_{n+k}\ est donnée par

\mathbb{P}\left(X_{n+k}=j\right)=\sum_{i\in E}\mathbb{P}\left(X_{n}=i\right)p^{(k)}_{i,j}.

En particulier,

\mathbb{P}\left(X_{n}=j\right)=\sum_{i\in E}\mathbb{P}\left(X_{0}=i\right)p^{(n)}_{i,j}.

En écriture matricielle, si la loi de \scriptstyle\ X_{n}\ est considérée comme un vecteur-ligne \scriptstyle\ \mu_{n}=(\mu_{n,i})_{i\in E}, avec \scriptstyle\ \mu_{n,i}=\mathbb{P}\left(X_{n}=i\right), cela se reformule en :

\mu_{n+k}=\mu_{n}P^k\quad\text{ et }\quad \mu_{n}=\mu_{0}P^n.
Propriété de Markov faible
Notation
- Introduction - Propriété de Markov faible - Classification des états - Probabilités de transition - Notation - Loi stationnaire - Illustration de l'impact du modèle - Exemple : Doudou le hamster - Applications
miniature
Voici ce qui a causé les toutes premières inégalités de richesse 💰
miniature
Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊
miniature
Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭
miniature
Des cellules solaires flexibles battent des records d'efficacité ⚡
miniature
Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀
miniature
Record établi pour un transistor en diamant 💎
miniature
Les sursauts radio rapides trahissent enfin leur origine cosmique 📡
miniature
Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠
miniature
Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊
miniature
Les oscillations collectives des foules humaines denses 🔁
miniature
Une forme inconnue de la matière détectée au LHC ? ⚛️
miniature
Le sel, un facteur méconnu de l'obésité ? 🧂
miniature
L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀
miniature
Découverte tectonique majeure sous les Petites Antilles 🌍
miniature
1
Peut-on geler en chauffant ? ❄️
miniature
Une peau électronique pour doter les robots du sens du toucher 👌
miniature
Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳
miniature
Le cancer inscrit dans nos gènes dès la naissance ? 🧬
miniature
Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥
miniature
Le passé verdoyant du plus grand désert du monde 🐪
miniature
Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷
miniature
Des puces quantiques plus proches que jamais ⚡
miniature
1
Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬
miniature
En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊
miniature
Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️
miniature
Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜
miniature
Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️
miniature
Cette vitamine développe les fonctions cognitives du cerveau 🧠
miniature
Comment des impacts géants vaporisent les corps planétaires ☄️
miniature
Les Américains riches vivent moins longtemps que les Européens pauvres 💰
miniature
Attention à ce riz naturellement riche en arsenic 🍚
miniature
L'intelligence artificielle contre la mort subite 💀
miniature
L'inévitable formation d'un océan de magma basal sur Terre 🔥
miniature
Découverte d'une plante étrange sans chlorophylle 🌱
miniature
Existe-t-il des mélodies naturelles ? 🎶
miniature
Cette exoplanète présente une signature de vie bien plus forte que celle de la Terre 👽
miniature
L'origine énigmatique des rayons cosmiques les plus énergétiques ⚡
miniature
1
Le diagnostic de l'autisme remis en cause par l'intelligence artificielle 🩺
miniature
Imprimer en 3D avec la lumière du soleil ☀️
miniature
La pollution atmosphérique nuit gravement au cerveau 🧠
miniature
Le trou noir supermassif Ansky vient de se réveiller ⚫
miniature
1
Voici ce qui rend notre cerveau vraiment unique 🧠
miniature
Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩
miniature
Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬
miniature
La physique révèle les secrets d'un strike parfait au bowling 🎳
miniature
Le TDAH associé à la démence 🧠
miniature
Découverte d'une nouvelle forme d'intrication quantique, une première en 20 ans ⚛️
miniature
Le régime cétogène montre des surprises sur le cholestérol 🧐
miniature
Un tango observationnel révèle une Super-Terre 🔭
miniature
Cette expérience montre que la graisse brune augmente fortement la longévité 🕒
Page générée en 0.146 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise