Carré - Définition

Construction au compas seul

On souhaite construire le carré de sommets ABCD connaissant seulement les points A et B. Posons R la distance entre Aet B ; alors, on procède comme suit :

• On trace C₁le cercle de centre A et de rayon R (qui contient alors B)

on a un troisième point du carré sur cette courbe.

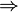
• On trace C₂ le cercle de centre B et de rayon R (qui contient alors A)

le quatrième point du carré se trouve sur cette courbe.

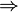
• Posons G un point d'intersection de C₁ avec C₂ ; on construit alors C₃ centré en G et de rayon R. Ce cercle intersecte C₁ en B et en un autre point H.
• C₄, de centre H et de rayon R, intersecte C₁ en G et en un nouveau point I.
• Posons S la distance entre G et I ; on construit alors C₅ de centre I et de rayon S (il contient forcément G).
• C₆ s'obtient en prenant pour centre B et pour rayon S (il contient forcément H). On note J le point d'intersection entre C₆ et C₅ qui est du même côté que G par rapport à la droite AB.
• Si T est la distance entre A et J, on construit C₇ le cercle de centre A et de rayon T (il contient forcément J).

Le point C est obtenu par intersection entre C₇ et C₂.

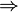
• On construit alors C₈ de centre C et de rayon R.

L'intersection de C₈ et C₁ est le point D.

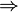
Symétries

Les transformations laissant un carré invariant sont de deux types :

• les symétries axiales, dont l'axe est soit une diagonale du carré, soit une médiatrice d'un côté ;
• les rotations dont le centre est le centre du carré et dont l'angle est un multiple de l'angle droit.

En voici la liste, elles sont au nombre de huit et forment un groupe :

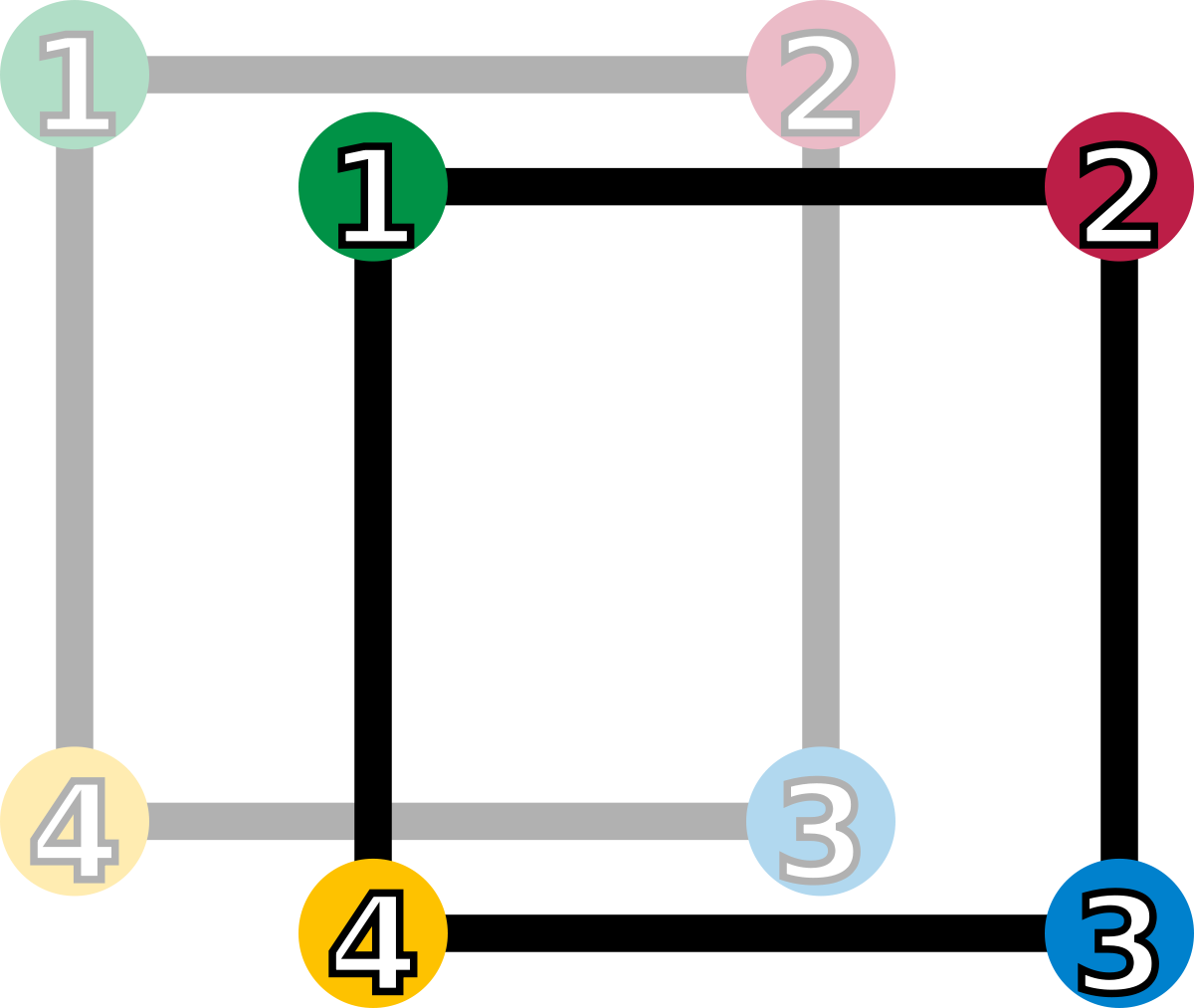
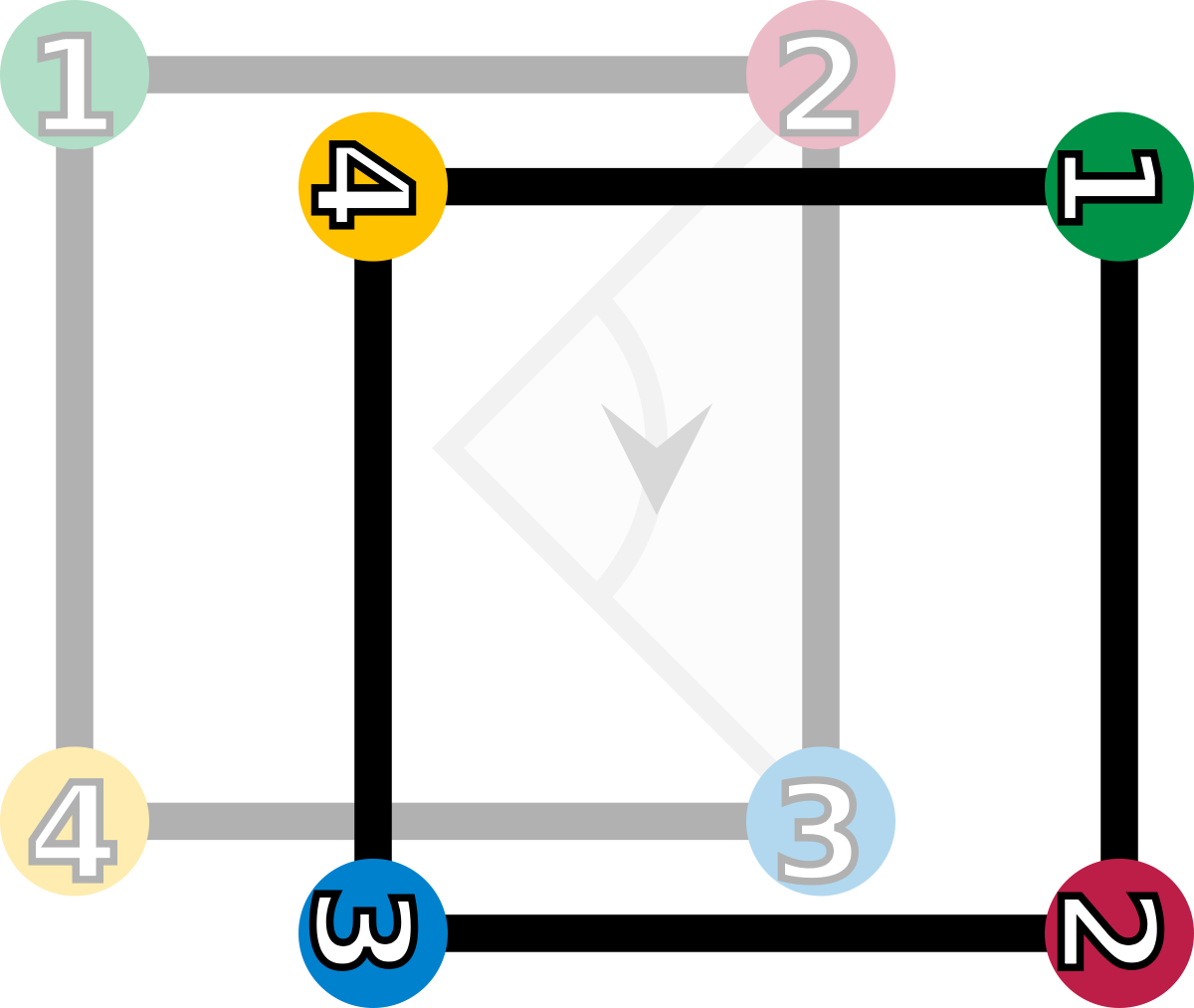
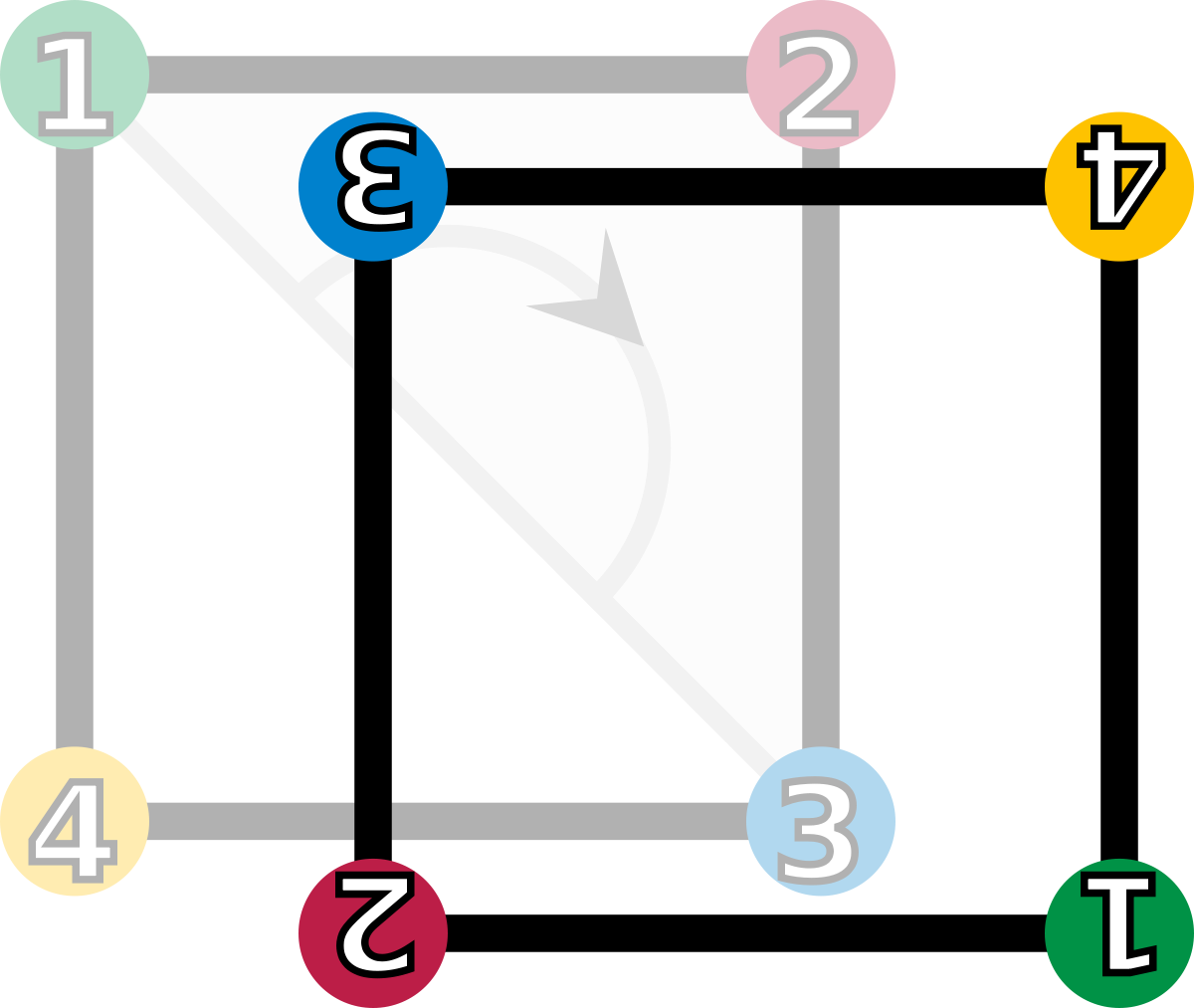
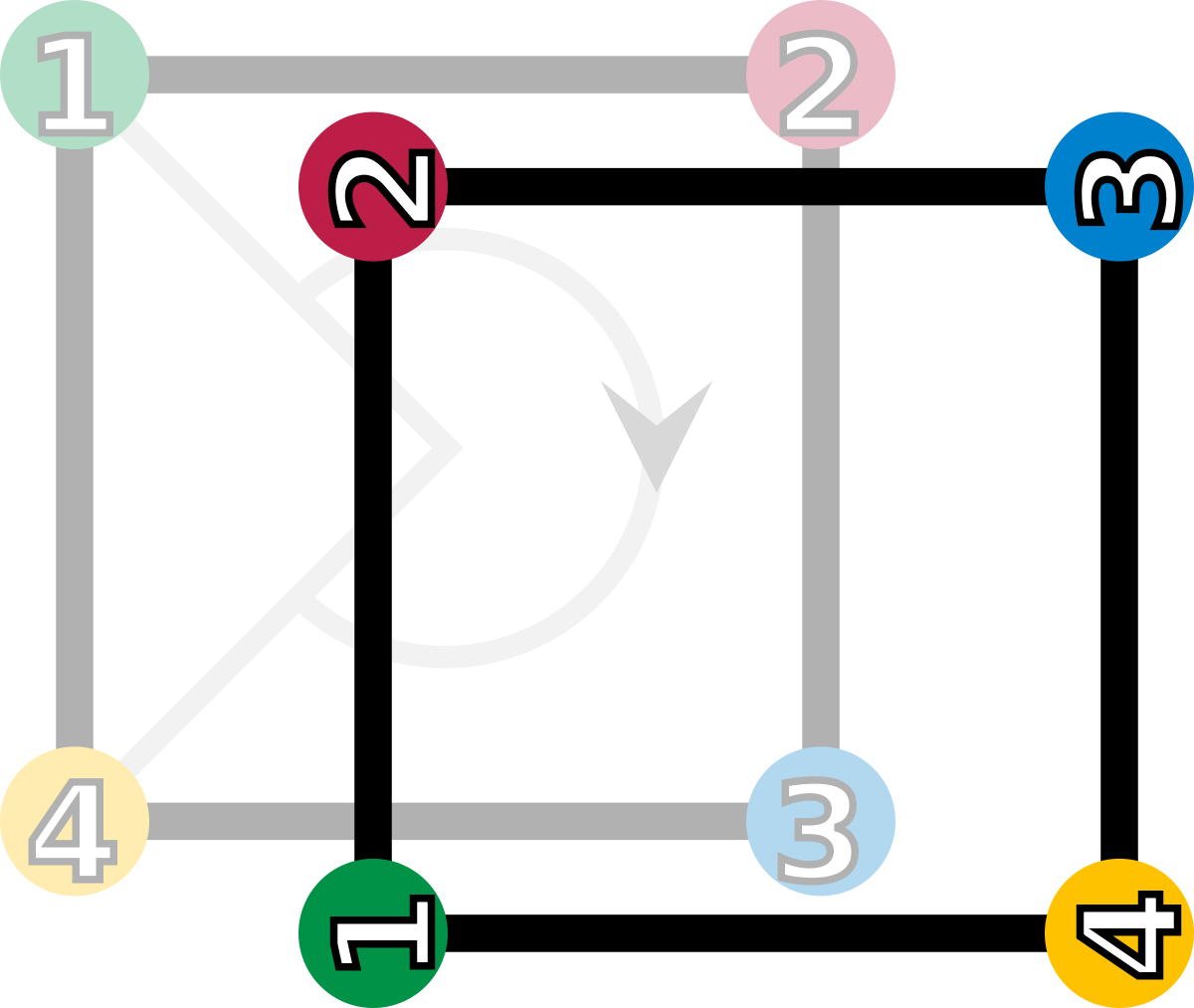
id (identité : chaque point est conservé)	r1 (rotation de 90° vers la droite)	r2 (rotation de 180°)	r3 (rotation de 270° vers la droite)
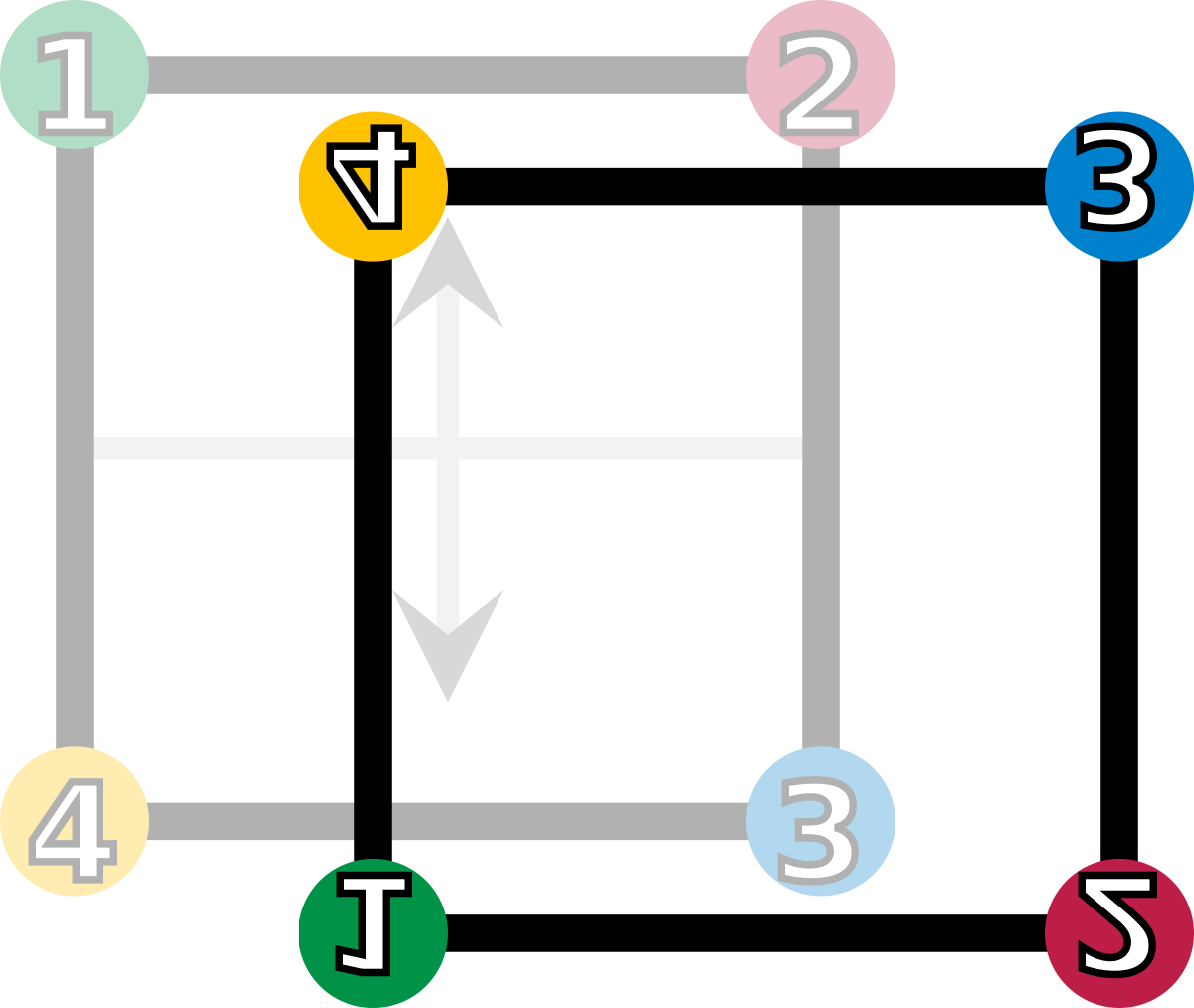
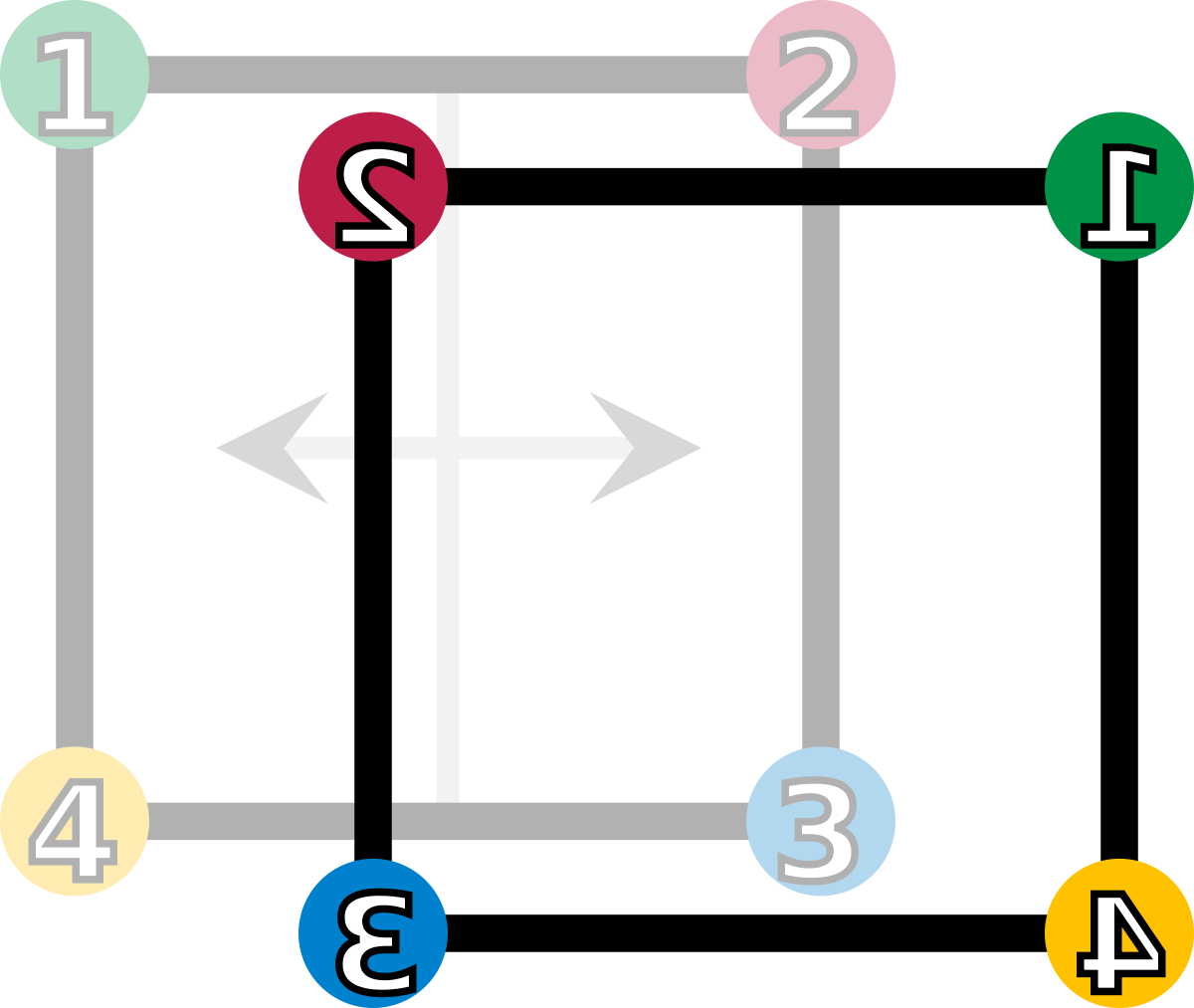
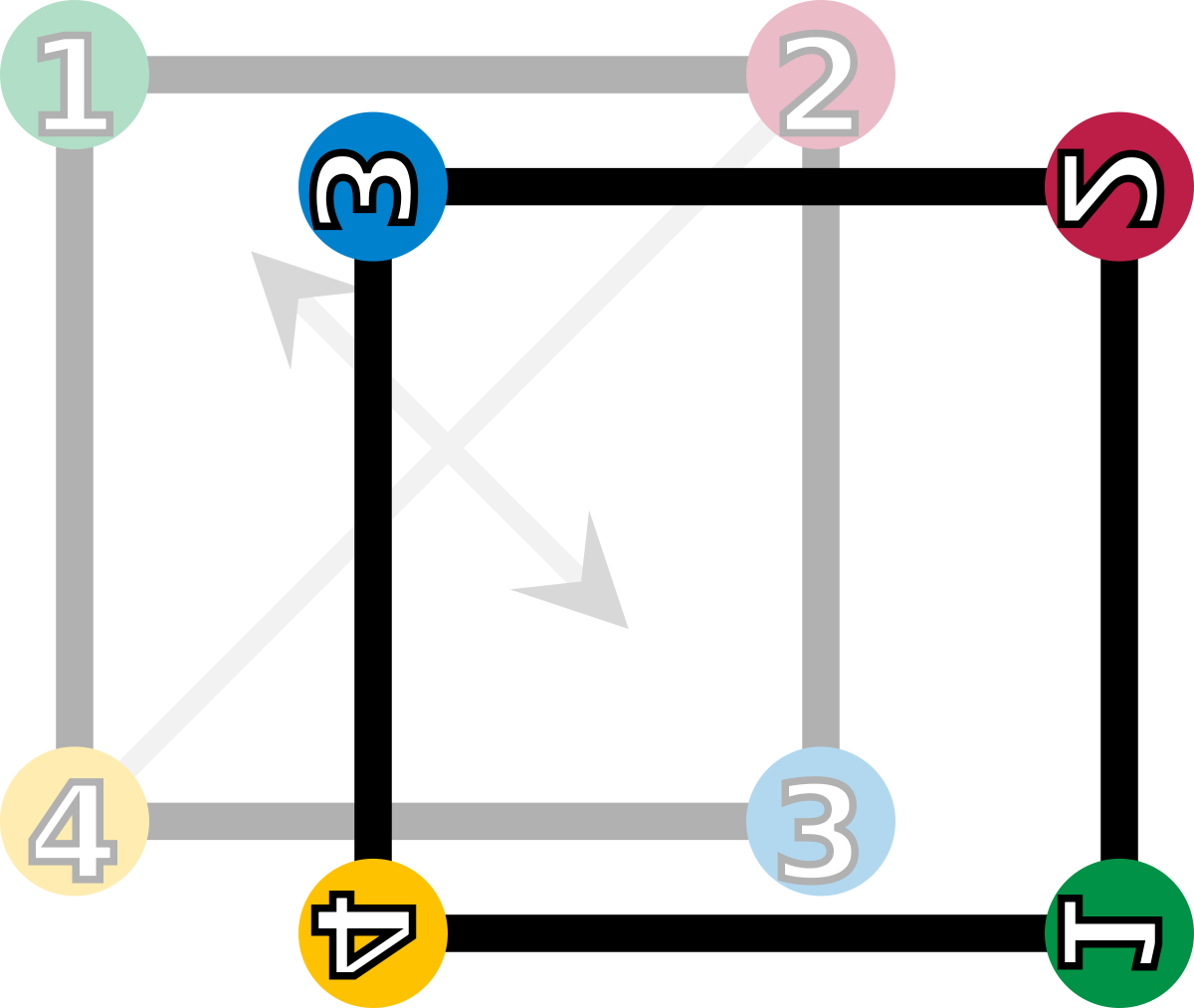
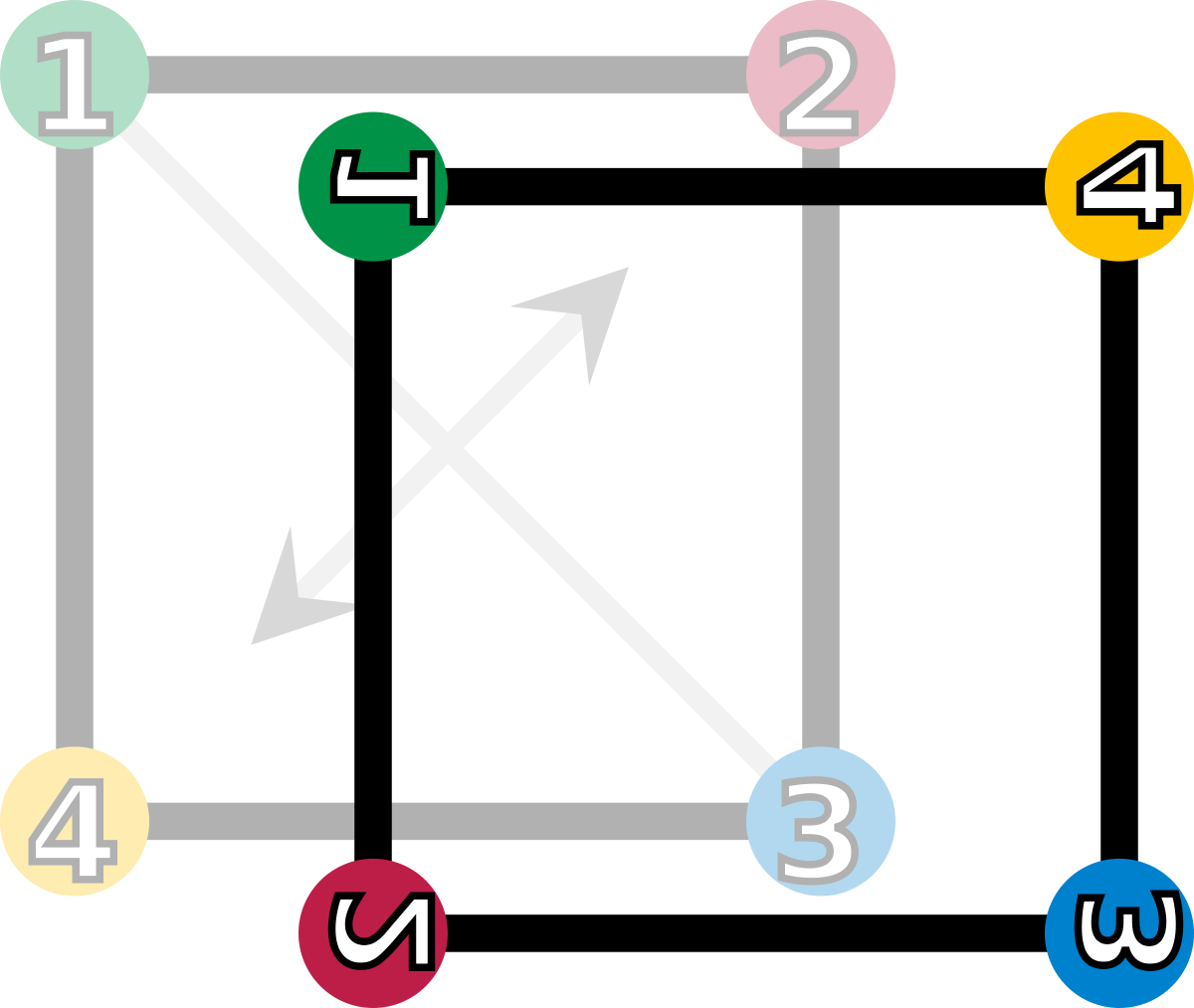
fv (retournement vertical)	fh (retournement horizontal)	fd (retournement suivant la première diagonale)	fc (retournement suivant la deuxième diagonale)
Les éléments du groupe de symétrie (D4). Les sommets sont colorés et numérotés uniquement pour visualiser les transformations.

Toute droite passant par O divise le carré en deux parties superposables.

Histoire

La tablette d'argile YBC 7289 : une très ancienne (environ 1700 avant J.-C.) représentation d'un carré avec ses diagonales et une valeur approchée de √2 (crédits : Bill Casselman).

Des poteries décorées de carrés sont attestées dès le VI^e millénaire av. J.-C. en Mésopotamie.

Des tablettes démontrent la connaissance des symétries et rotations du carré vers le XVIII^e siècle av. J.-C.. La tablette BM 15285 contient une quarantaine de problèmes mathématiques concernant des aires de figures liées à des carrés.

Le Talmud recommande de bâtir des villes de forme carrée, quelle que soit la forme de son enceinte.