Carré magique (mathématiques) - Définition

Méthodes de construction

En 2010, il n'existe pas une méthode unique permettant de construire à la fois les carrés magiques d'ordre pair et d'ordre impair. Cependant, il existe plusieurs méthodes directes pour construire les carrés d'ordre impair et les carrés d'ordre pair.

Parmi les méthodes de construction indirectes, il en existe au moins trois. La multiplication de carrés magiques en est une (voir la section ). Si un carré magique est déjà construit, il est possible d'en dériver d'autres par permutations de ses colonnes et de ses rangées. Finalement, il est possible d'en créer un autour d'un carré magique déjà construit : c'est le carré magique à enceinte.

Ordre impair

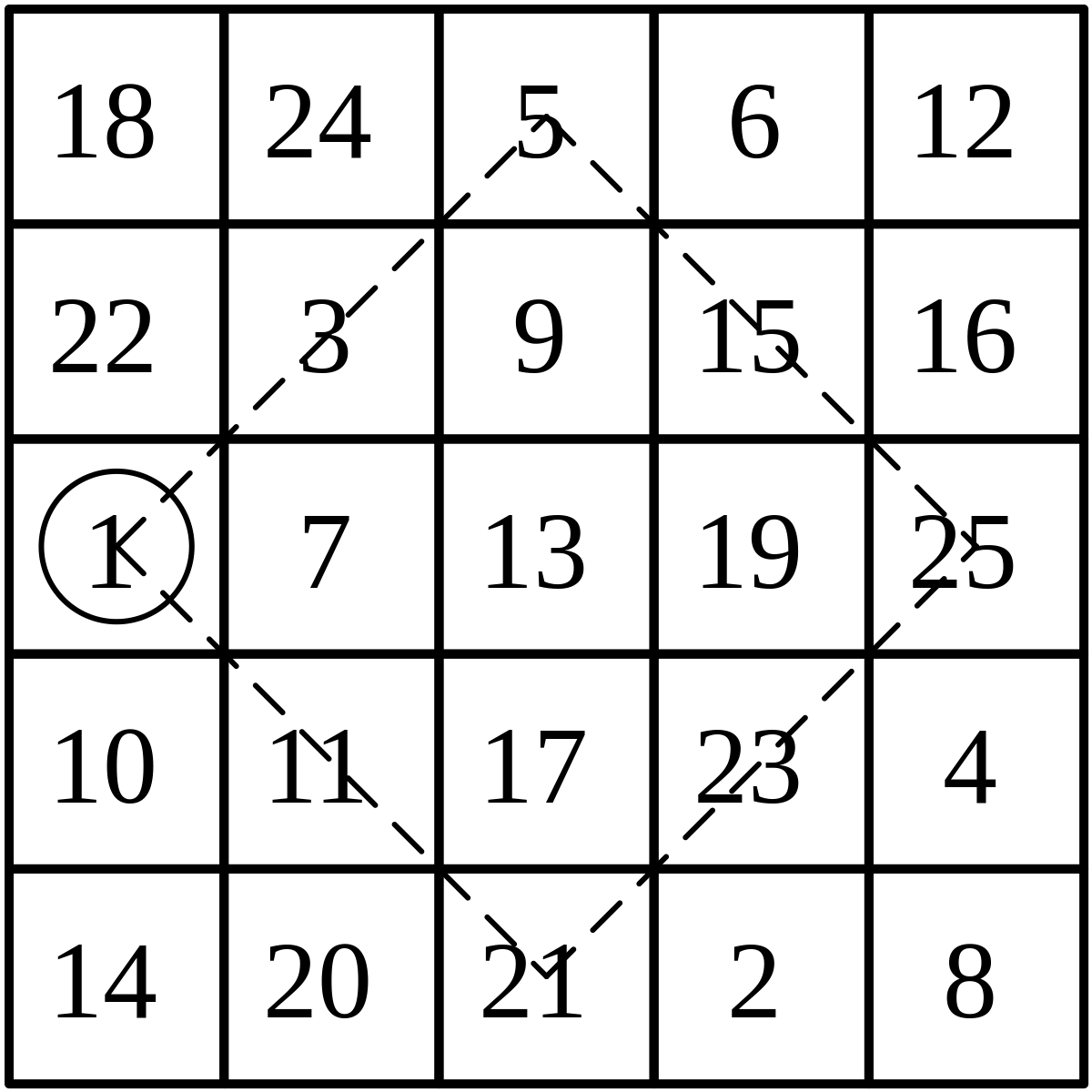
Méthode du damier crénelé

Cette méthode de construction a été publiée en 1612 par Claude-Gaspard Bachet de Méziriac dans Problèmes plaisants et délectables qui se font par les nombres. Elle se base sur un damier crénelé.

Par exemple, pour un carré magique de côté 5 :

Premières étapes de construction d'un carré magique d'ordre 5. Chaque diagonale allant de gauche à droite comporte un entier unique en ordre croissant. Ensuite, le contour du carré magique final est esquissé.

Dernières étapes de construction d'un carré magique d'ordre 5. Chaque case qui se trouve en-dehors du contour est « glissé » de 5 places en direction du centre. Une fois les déplacements effectués, le carré magique final est complet.

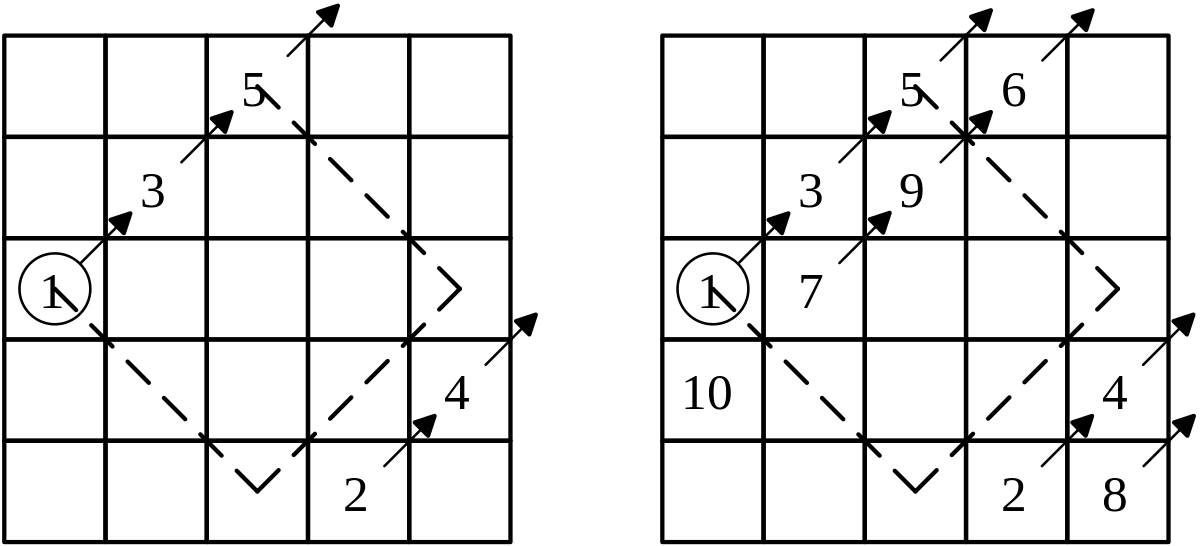
Méthode siamoise

La méthode siamoise a été introduite en France par Simon de La Loubère en 1688 alors qu'il revenait de son ambassade au Siam.

Construction d'un carré magique d'ordre impair selon la méthode siamoise.

Dans cet exemple, le carré est rempli selon les diagonales nord-est (NE), mais elles pourraient être parallèles à sud-est (SE), à sud-ouest (SO) ou à nord-ouest (NO).

1) Placer le 1 tel que montré.

2) Décaler d'une case vers la droite puis d'une case vers le haut pour le 2, et ainsi de suite pour le 3, puis le 4, etc.

3) Si la pointe de la flèche sort du carré, revenir de l'autre côté, comme si le carré était enroulé sur un tore.

4) Si la prochaine case est occupée, décaler d'une case vers le bas.

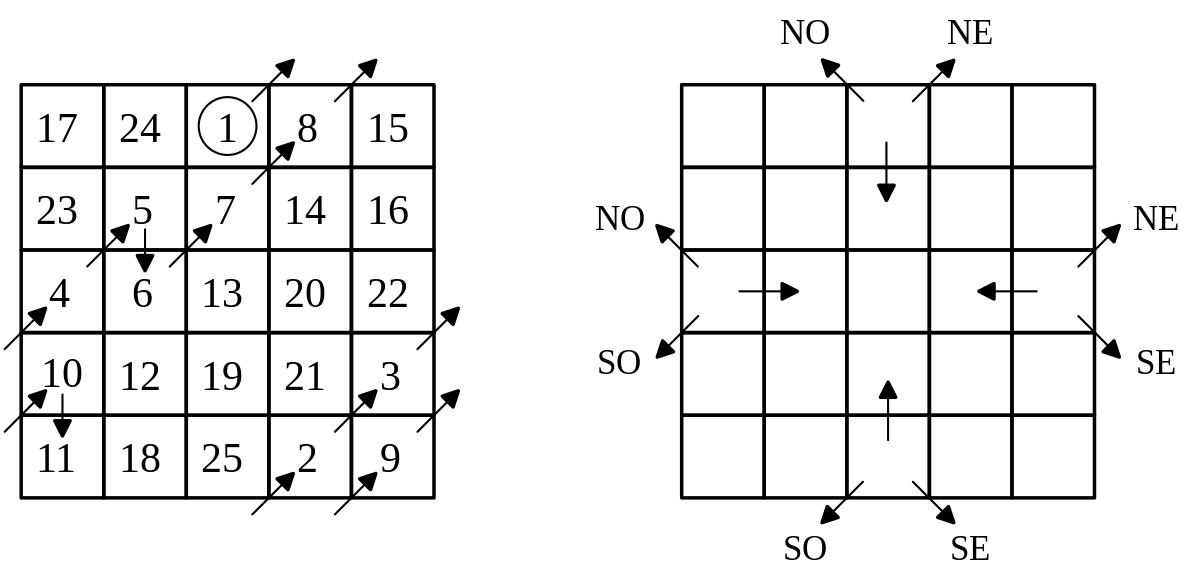
La méthode exposée par de la Loubère peut être généralisée. Supposons que nous nous déplacions dans un plan cartésien. Dans la figure plus haut, aller en diagonale vers la droite et vers le haut revient à effectuer la translation (1,1). Lorsqu'il y a une collision, c'est-à-dire que la prochaine case est occupée, il y a une translation (0,-1). Philippe de La Hire a établi les conditions pour lesquelles un carré d'ordre N est magique. Les coordonnées du vecteur « déplacement » (C, L) et du vecteur « collision » (C + c, L + l) doivent respecter les conditions suivantes :

1. C, c, L et l sont des entiers relatifs tous différents de zéro (par exemple, -7, 9 ou 4), mais leur somme peut égaler zéro (par exemple, C = -6 et c = 6).
2. C, c, L et l sont tous premiers avec N (par exemple, 3 est premier avec 11, mais pas avec 15).
3. (C × l) - (c × L) est premier avec N.

De plus, le carré ainsi construit est diabolique si :

1. (C + L) et (c + l) sont tous deux premiers avec N (les diagonales brisées allant de la gauche en haut à la droite en bas égalent la constante magique), et
2. (C - L) et (c - l) sont tous deux premiers avec N (les diagonales brisées allant de la droite en haut à la gauche en bas égalent la constante magique).

Un carré magique d'ordre 5 construit selon la méthode de Moschopoulos.

Par exemple, la méthode de construction proposée par le Byzantin Manuel Moschopoulos, dite « parcours en cavalier d'échecs », se représente par le vecteur déplacement (1, 2) et le vecteur collision (1 + 1, 2 - 2) = (2, 0).

Méthode du lozenge

Les nombres impairs sont inscrits de manière à former un losange au « centre » du carré, d'où le nom de la méthode publiée par John Horton Conway.

1. Les nombres impairs 1, 3 et 5 sont inscrits selon une diagonale montante qui va de gauche à droite. 2. Les nombres pairs 2 et 4 sont ensuite inscrits pour compléter la diagonale brisée. 3. « Descendre » à la prochaine diagonale. 4. Recommencer avec les nombres suivants.

Le résultat final est un carré magique dont la constante est 65.

Ordre pair

Créer des carrés magiques d’ordre pair est plus difficile. Certaines méthodes permettent de construire :

1. des carrés magiques d'ordre pairement pair (divisible par 2 et par un nombre pair), par exemple :
   1. méthode des permutations autour des diagonales
   2. méthode de W. S. Andrews
2. des carrés magiques d'ordre pairement impair (divisible par 2 et par un nombre impair), par exemple :
   1. méthode LUX de John H. Conway
3. des carrés magiques dont l'ordre est divisible par 8, par exemple :
   1. méthode de Benjamin Franklin
4. des carrés magiques d'ordre pair, par exemple :
   1. méthode de de La Hire
   2. méthode de Strachey.

Selon Gérardin, 1986, la méthode de Strachey est la plus générale. Par contre, elle s'appuie sur des carrés magiques déjà construits et ne peut servir à construire des carrés magiques d'ordre 4. Par ailleurs, la méthode de Benjamin Franklin crée des carrés magiques possédant de multiples propriétés. Pour ces raisons, plusieurs méthodes seront présentées dans cette section. Ensemble, elles permettent de construire n'importe quel carré d'ordre pair.

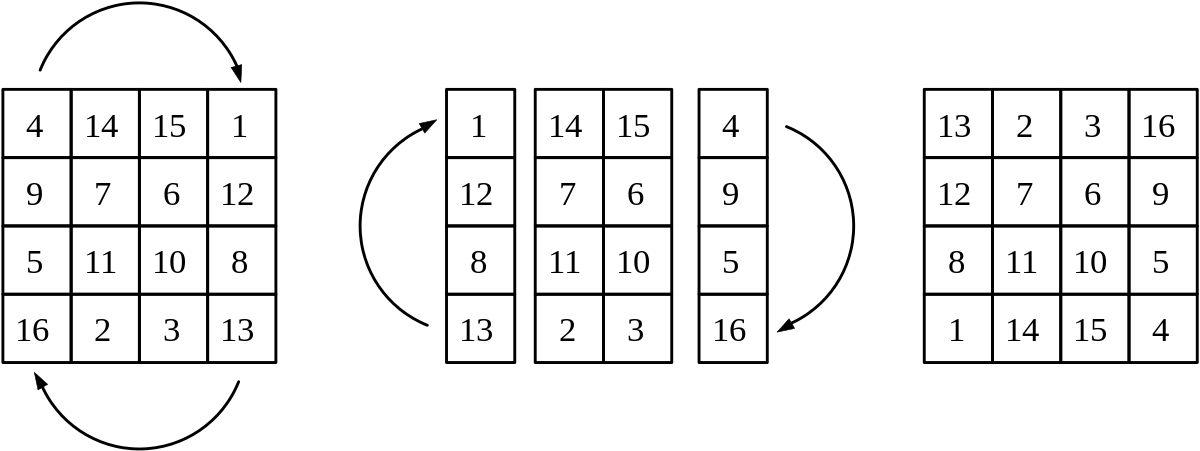
Méthode des permutations autour des diagonales

Cette méthode sert à construire des carrés d'ordre pairement pair (4, 8, 12...). Elle se base sur l'observation que ces carrés « se laissent aisément couper et recouper par moitié », ils possèdent donc « des propriétés géométriques de symétrie » :

1. Soit une grille vide d'ordre N, celui-ci valant 4, 8, 12...
2. Dans cette grille, inscrire les nombres naturels dans l'ordre : 1, 2, 3... Il y a donc N² nombres à inscrire (16, 64, 144...).
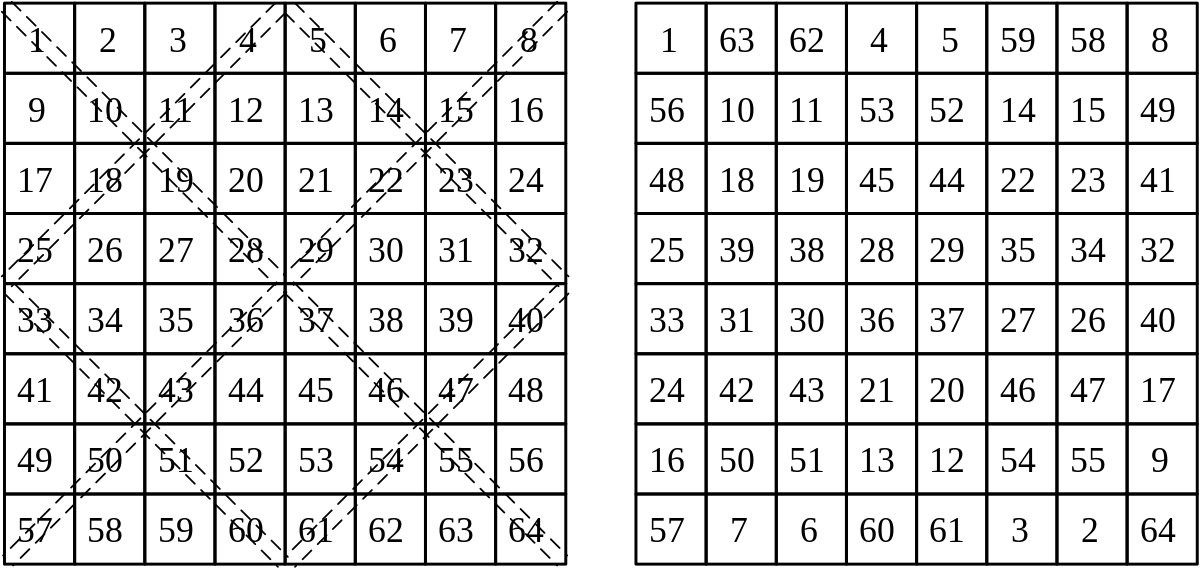
3. Le damier ainsi construit est composé de 1, 4, 9... sous-damiers d'ordre 4. Dans chacun de ces sous-damiers, tracer une ligne passant par les deux diagonales principales.
4. Remplacer chaque nombre n qui n'est pas recouvert par son complément qui vaut (N² + 1) - n. Par exemple, pour un carré magique 8x8, N vaut 8, le complément de 2 est donc (8² + 1) - 2 = 65 - 2 = 63.

Construction d'un carré magique d'ordre 8. Dans le carré de gauche, les nombres naturels sont inscrits dans l'ordre. De plus, les diagonales principales de chaque sous-damier 4x4 sont recouvertes de lignes en pointillés. À droite, le carré final, magique, est inscrit. Chaque nombre qui n'était pas recouvert par une ligne en pointillés a été remplacé par son complément à (8² + 1) = 65.

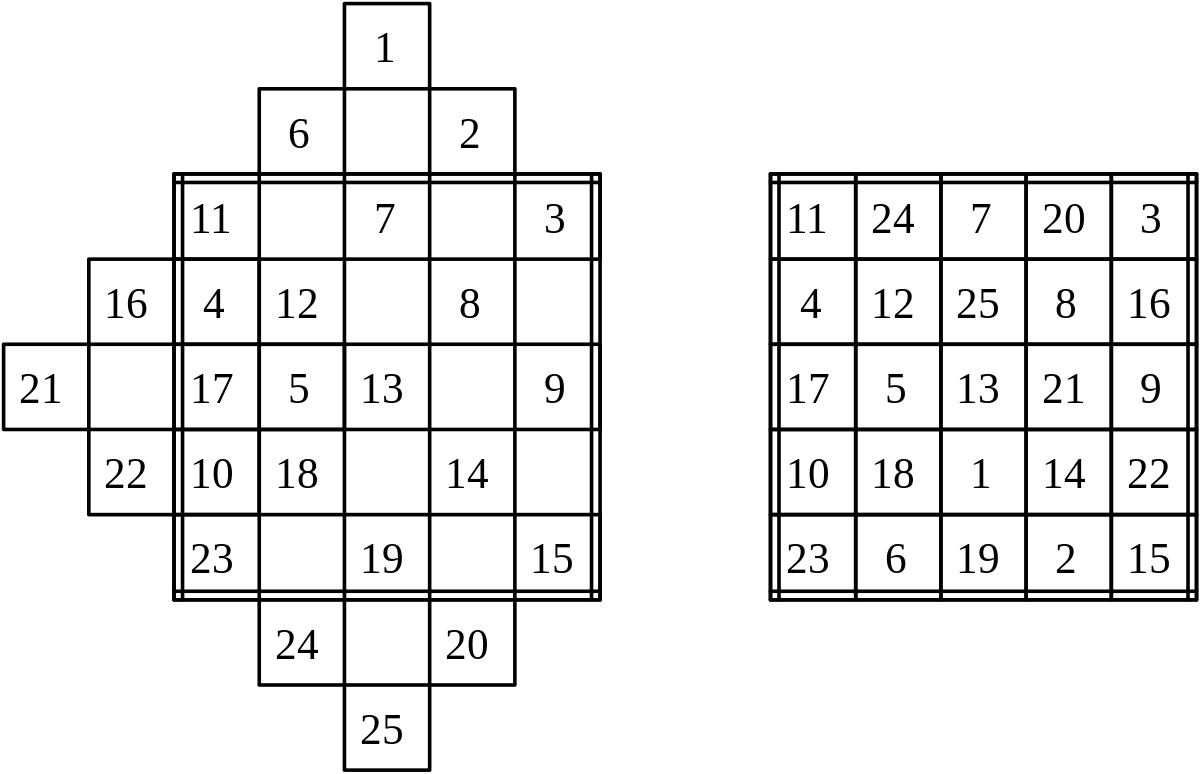
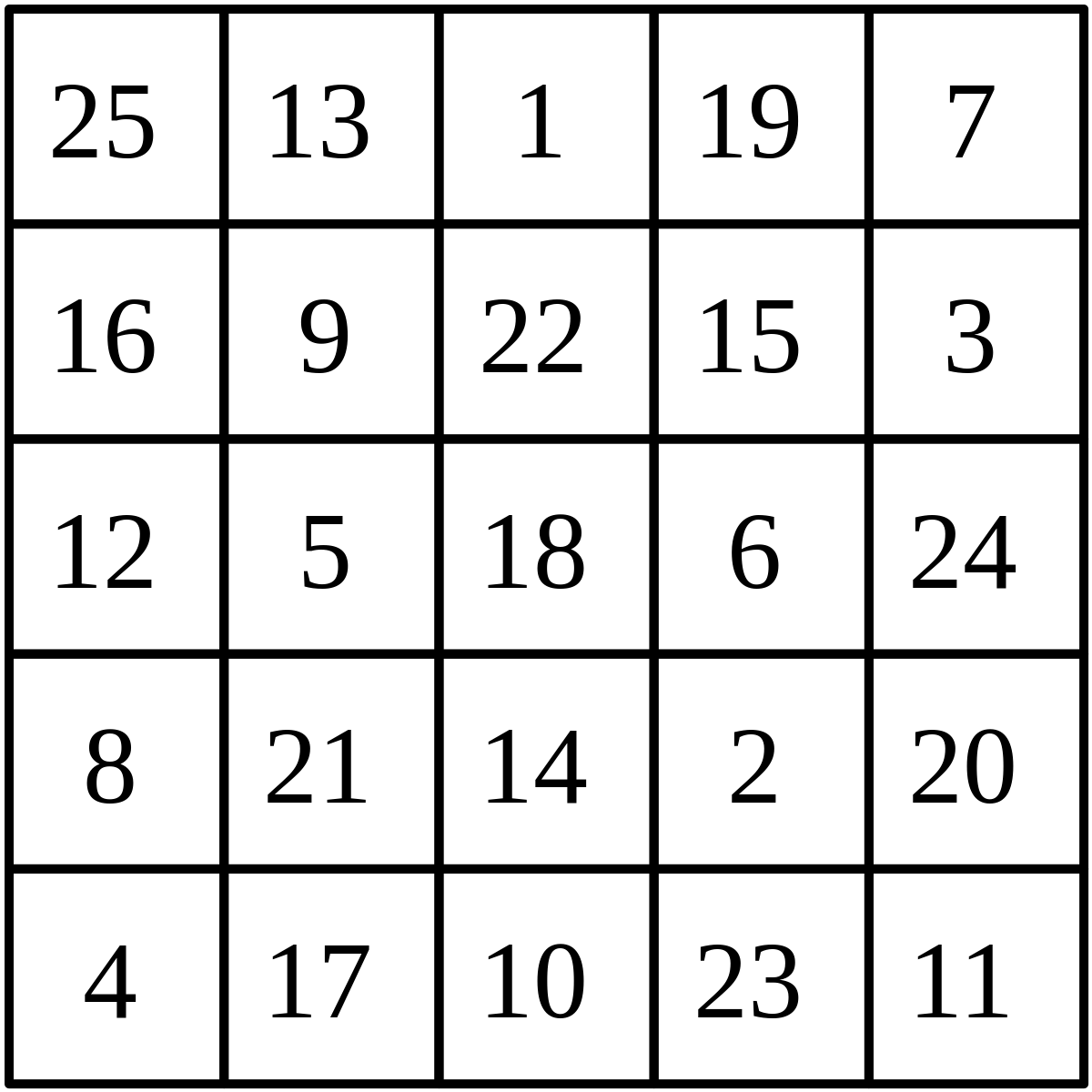
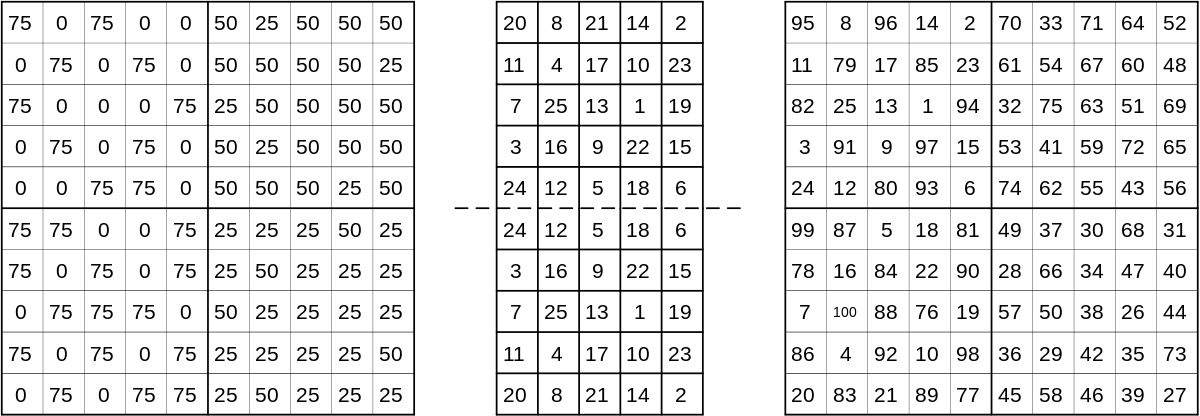
Méthode de Strachey

Cette méthode, initialement publiée par Ralph Strachey et ensuite présentée sous une « forme élégante » par William H. Benson et Oswald Jacoby, permet de construire des carrés magiques d'ordre pair, mais elle ne permet pas de tous les construire. Cependant, le nombre de carrés magiques ainsi construits est très élevé. Par exemple, le nombre de carrés magiques d'ordre 5 s'élève à 275 305 224 et la méthode de Strachey permet de créer, au minimum, un carré magique différent d'ordre 10 à partir de chacun de ces carrés magiques.

Puisque le damier est d'ordre pair, il est toujours divisible en quatre sous-damiers que nous nommons A, B, A' et B'. Soit N l'ordre du carré magique.

Si N ÷ 2 est impair 

1. Poser N = 2 × (2n + 1).
2. Chaque rangée du sous-damier A contient exactement n fois le nombre 3. Les autres cases contiennent 0.
3. Dans le sous-damier A, la diagonale qui va de haut à gauche en bas à droite contient exactement (n + 1) fois le nombre 3.
4. Dans le sous-damier A', remplir les cases « en miroir » (selon la ligne de séparation) en se basant sur les cases de A.
5. Chaque rangée du sous-damier B contient exactement (n + 2) fois le nombre 2. Les autres cases contiennent le nombre 1.
6. Dans le sous-damier B, la diagonale qui va de haut à droite en bas à gauche contient exactement (n + 2) fois le nombre 2.
7. Dans le sous-damier B', remplir les cases « en miroir » en se basant sur les cases de B.

Carrés servant à construire un carré magique d'ordre 10. Le carré est divisé en quatre parties égales.

1. Ici, 10 = 2 × (2n + 1). Donc, n = 2.

2. Chaque rangée du sous-damier A contient 2 fois le nombre 3. Les autres cases contiennent 0.

3. Dans le sous-damier A, la diagonale qui va du haut à gauche au bas à droite contient 3 fois le nombre 3.

4. Le sous-damier A étant rempli, remplir le sous-damier A' « en miroir » (la ligne de séparation fait office de miroir en quelque sorte).

5. Chaque rangée du sous-damier B contient 4 fois le nombre 2.

6. Dans le sous-damier B, la diagonale qui va du haut à droite au bas à gauche contient également 4 fois le nombre 2.

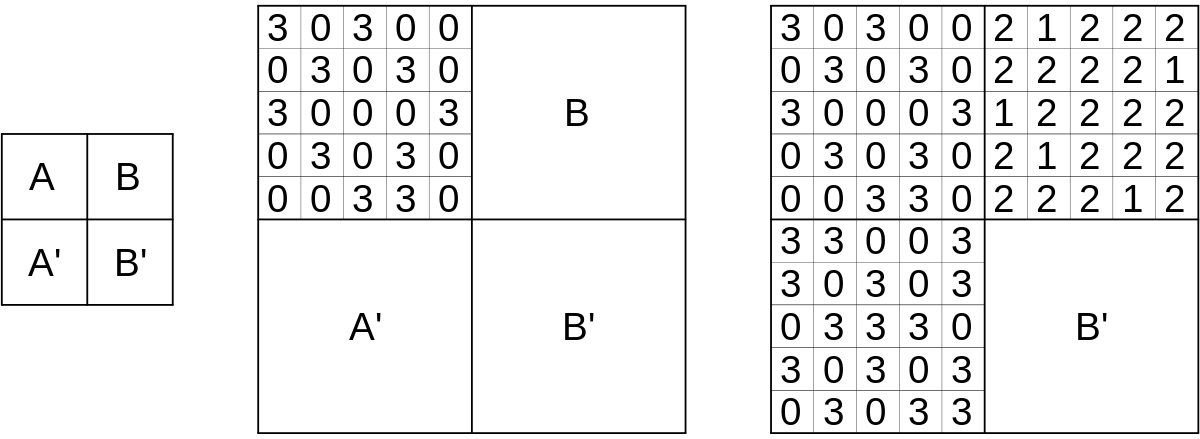
8. Multiplier chaque case par le quart de N².
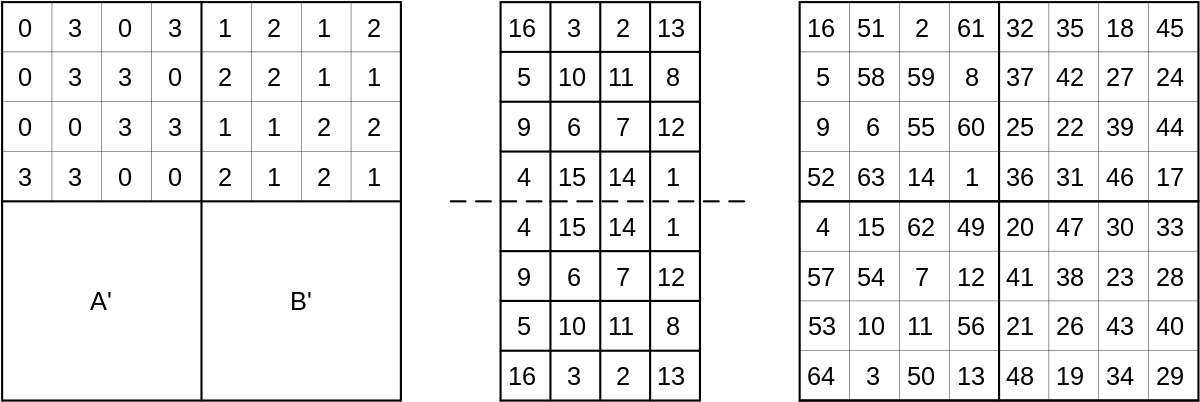
9. Choisir n'importe quel carré magique d'ordre 2n + 1 (impair).
10. Créer une image « miroir » de ce carré et la glisser sous le carré magique initial, formant ainsi un rectangle vertical.
11. Additionner les cases de ce rectangle aux cases des sous-damiers A, B, A' et B'.
12. Le carré final est magique.

Dernières étapes menant à un carré magique d'ordre 10.

8. Chaque case est multipliée par 10 × 10 ÷ 4 = 25.

9. Un carré magique d'ordre 5 a été choisi (et son image a été inscrite).

10. Les cases des carrés magiques sont additionnées.

11. Le résultat apparaît.

Si N ÷ 2 est pair 

1. Poser N = 2 × (2n).
2. Chaque rangée du sous-damier A contient exactement n fois le nombre 3. Les autres cases contiennent 0.
3. Dans le sous-damier A, la diagonale qui va de haut à gauche en bas à droite contient exactement n fois le nombre 3.
4. Dans le sous-damier A', remplir les cases « en miroir » (selon la ligne de séparation) en se basant sur les cases de A.
5. Chaque rangée du sous-damier B contient exactement n fois le nombre 2. Les autres cases contiennent le nombre 1.
6. Dans le sous-damier B, la diagonale qui va de haut à droite en bas à gauche contient exactement n fois le nombre 2.
7. Dans le sous-damier B', remplir les cases « en miroir » en se basant sur les cases de B.

8. Multiplier chaque case par le quart de N².
9. Choisir n'importe quel carré magique d'ordre 2n (pair).
10. Créer une image « miroir » de ce carré et la glisser sous le carré magique initial, formant ainsi un rectangle vertical.
11. Additionner les cases de ce rectangle aux cases des sous-damiers A, B, A' et B'.
12. Le carré final est magique.

Carrés servant à construire un carré magique d'ordre 8. Se reporter aux explications du carré magique 10x10 construit par la même méthode pour plus de détails.

A. Ici, 8 = 2 × (2n). Donc, n = 2. De plus,

B. Chaque rangée du sous-damier A contient 2 fois le nombre 3. Les autres cases contiennent 0.

C. Dans le sous-damier A, la diagonale qui va du haut à gauche au bas à droite contient 2 fois le nombre 3.

D. Chaque rangée du sous-damier B contient 2 fois le nombre 2.

E. Dans le sous-damier B, la diagonale qui va du haut à droite au bas à gauche contient également 2 fois le nombre 2.

F. Un carré magique d'ordre 4 est choisi et son image apparaît en-dessous.

G. N² = 64. Son quart vaut 16.

H. Le carré final est magique.

Permutations des colonnes et des rangées

Par convention, la rotation ou la réflexion d'un carré magique ne crée pas de nouveau carré. Par contre, « [en] échangeant deux colonnes et deux lignes (symétriquement placés par rapport au centre) d'un carré magique, on obtient un nouveau carré magique, cousin en quelque sorte du carré initial ». Cette méthode de permutations des colonnes et des rangées est valable tant pour les carrés d'ordre pair qu'impair.

Un carré magique d'ordre 4 est utilisé pour démontrer comment permuter des colonnes et des rangées dans le but d'obtenir un nouveau carré magique.

Méthode des enceintes

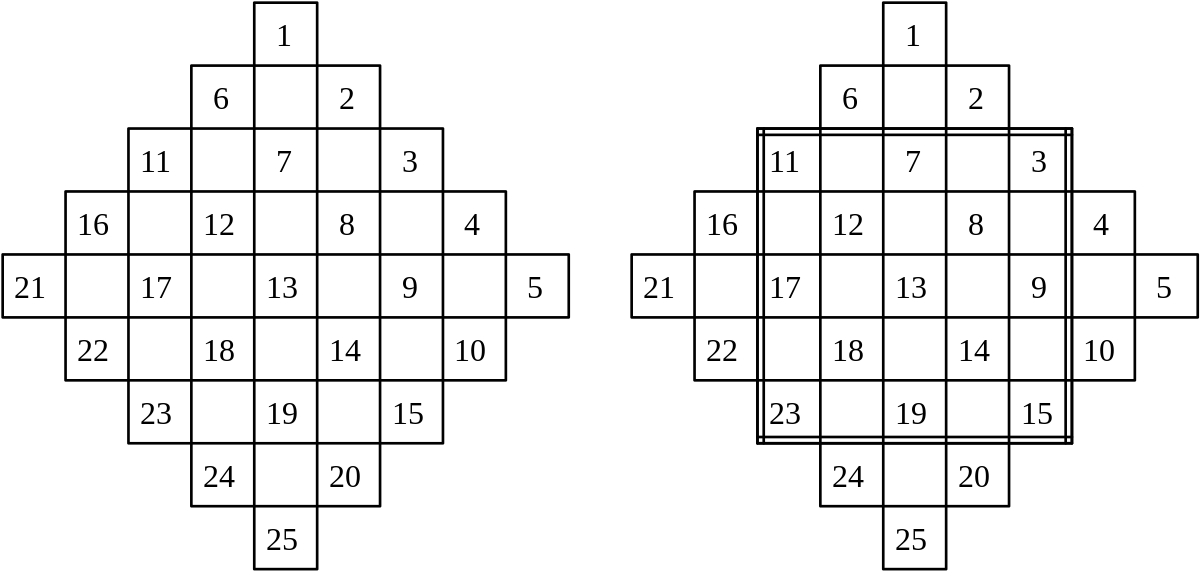
En entourant un carré magique non normal d'une enceinte, c'est-à-dire d'une rangée de cases, il est possible de créer un carré magique normal. Cette méthode est due à Frénicle. Pour les besoins de l'explication, nous travaillerons avec deux carrés magiques de taille définie, mais la méthode est relativement facile à généraliser :

1. Choisir un carré magique normal d'ordre 3. Appelons-le « carré central ».
2. Entourer le carré central d'une rangée de cases vides, elles forment l'enceinte.
3. Le carré magique à enceinte sera d'ordre 3 + 2 = 5, car l'enceinte borde au complet le carré central. Appelons-le « carré à enceinte ».
4. Le nombre de cases dans le carré central est 3², alors qu'il est de (3 + 2)² dans le carré à enceinte. L'enceinte contiendra donc cases.
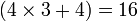
5. En « passant » d'un carré 3x3 à un carré 5x5, la constante magique doit passer de 15 à 65.
6. Sachant qu'il faut placer la suite de nombres 1, 2... 23, 24, 25 dans le carré à enceinte et observant que la constante magique a augmenté de 50, il faut modifier les nombres dans le carré central. Avant de procéder, un observation supplémentaire s'impose. La méthode ne fonctionne que si les nombres du carré central sont « au milieu » de la suite de nombres, c'est-à-dire 9, 10, 11... La valeur exacte à ajouter à chaque nombre du carré central est 3² − 1 = 16. Le carré ainsi produit est non normal, mais est toujours magique.
7. Il reste à placer les nombres « extrêmes » de la suite : 1, 2, 3... 8 et 18, 19 ... 25. Avant de procéder, une observation va éliminer plusieurs possibilités. La constante magique du carré central non normal est de . La constante magique du carré à enceinte est de 65. La différence, 65 − 39 = 26, doit provenir des cases dans l'enceinte. Or, les seules sommes pouvant donner ce résultat sont 1 + 25, 2 + 24... Ces paires doivent donc être placées de façon symétrique relativement au centre du carré.
8. En ce qui concerne l'arrangement des nombres dans les colonnes et les rangées de l'enceinte, le lecteur peut procéder par essai et erreur. Pour des carrés magiques à enceinte plus grands, il vaut mieux y aller de façon systématique (voir par exemple ).