Capacité thermique massique - Définition
La liste des auteurs de cet article est disponible ici.
Cas des solides
Valeurs courantes
| Substance (phase solide) | Capacité thermique massique J·kg-1·K-1 |
|---|---|
| Asphalte | 920 |
| Brique | 840 |
| Béton | 880 |
| Granite | 790 |
| Gypse | 1090 |
| Marbre | 880 |
| Sable | 835 |
| Bois | ≈ 1200-2700 |
Cas des solides cristallisés
Dans le cas des solides, à suffisamment haute température, la loi de Dulong et Petit est applicable et permet notamment retrouver que, à basse température,
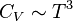
Les coefficients de dilatation des corps solides et liquides sont généralement suffisamment faibles pour qu'on néglige la différence entre Cp et CV pour la plupart des applications.
| Substance | Θ (K) |
|---|---|
| Al | 398 |
| C (diamant) | 1860 |
| Cu | 315 |
| Fe | 420 |
| K | 99 |
| Pb | 88 |
Suivant la théorie de Debye, la capacité thermique molaire d'un corps simple solide peut être déterminée au moyen de la formule :
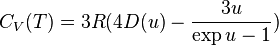
avec
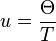
Θ est la température de Debye, qui est une caractéristique de chaque substance,
R est la constante molaire des gaz,
et
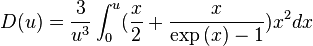
Cette formule se simplifie à basse température, ainsi qu'à haute température ; dans ce dernier cas, nous retrouvons la loi de Dulong et Petit :

La théorie n'est plus valable pour les corps composés.
Formules empiriques
Pour des corps purs (solides, liquides ou gazeux) et à pression constante, 2 formules empiriques à 3 paramètres ont pu être dégagées, pour un intervalle de température donné :
Cp = a + bT + cT2 ou bien Cp = a' + b'T + c'T − 2.
Les valeurs des coefficients sont indiqués dans des tables et sont caractéristiques d'un corps donné.
Pour le bois sec, par exemple, on a :
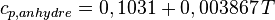
avec :
- cp,anhydre : exprimé en kJ·kg–1·K–1
- T : température thermodynamique (K).
À 20°C, on obtient 1236 J/kg.K pour le bois sec.
Pour le bois humide :
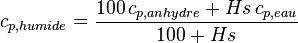
où Hs est la masse d'eau rapportée à la masse du bois sec en %.
Valeurs pour différentes substances
| Substance | Phase | Capacité thermique massique J·kg-1·K-1 |
|---|---|---|
| Air (sec) | gaz | 1005 |
| Air (saturé en vapeur d'eau) | gaz | ≈ 1030 |
| Aluminium | solide | 897 |
| Azote | gaz | 1042 |
| Cuivre | solide | 385 |
| Diamant | solide | 502 |
| Eau | gaz | 1850 |
| liquide | 4186 | |
| solide (0 °C) | 2060 | |
| Éthanol | liquide | 2460 |
| Fer | solide | 444 |
| Graphite | solide | 720 |
| Hélium | gaz | 3160 |
| Hexane | liquide | ≈ 2267.95 |
| Huile | liquide | ≈ 2000 |
| Hydrogène | gaz | 14300 |
| Laiton | solide | 377 |
| Lithium | solide | 3582 |
| Mercure | liquide | 139 |
| Octane | liquide | ≈ 1393.33 |
| Or | solide | 129 |
| Oxygène | gaz | 920 |
| Zinc | solide | 380 |

















































