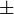Camshift - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le Camshift (Continuously Adaptive Mean Shift) est un algorithme de segmentation d'images couleur introduit par Gary Bradski en 1998, le Camshift exploite habilement l'algorithme du mean-shift en modifiant la taille de la fenêtre lorsque ce dernier est arrivé à convergence. Le Camshift couplé en est une adaptation aux séquences d'images couleur, et est exploité en poursuite d'objet en temps réel. Une implémentation gratuite de cet algorithme se trouve dans la bibliothèque logicielle de vision par ordinateur OpenCV.
Mean-Shift pour la détection de mode dans une densité 2D
Le mean-shift est une approche non-paramétrique permettant (entre autres) de détecter les modes d'une distribution de probabilité par une procédure récursive convergeant vers le point de stationnarité le plus proche. Cette approche tend à ignorer l'effet des outliers, compensant l'effet des distracteurs et des bruits de l'image.
Les modes à trouver sont les maxima locaux de la distribution spatiale f(x,y) = p(peau | x,y) de la probabilité de teinte chair dans l'image. L'approche du Mean-Shift est une procédure itérative consistant à déplacer sur la distribution f une fenêtre W, de taille fixe, de sa position (x0,y0) à la position (xc,yc) moyenne des points de f inclus dans W pondérés par leur valeur de probabilité.

Le mean shift est un algorithme robuste pour trouver les maxima d'une distribution de probabilité, où plus exactement le maxima le plus proche de sa position initiale. Toutefois, il nécessite de connaître la taille de l'objet recherché, qui est définie par l'utilisateur à l'initialisation du mean shift. La carte de probabilité est obtenue après une opération de rétroprojection d'un modèle de couleur, typiquement un histogramme (modèle non paramétrique) de la couleur que l'on cherche à isoler.
Les étapes de la détection d'un mode peuvent se résumer ainsi :
- I = f(x,y) image de probabilité de la couleur peau (Pskin) obtenue par rétroprojection d'un histogramme 32x32x32 dans l'espace colorimétrique HSV (pour l'exemple) construit off-line à partir d'une base d'exemples de pixels de couleur peau.
- Initialisation de la fenêtre W du mean shift: position et taille.
- Tant que W est déplacée de plus d'un certain seuil et que le nombre d'itérations maximal n'est pas atteint:
- calculer le barycentre des pixels (x, y) inclus dans la fenêtre, ainsi que leur somme (moment d'ordre zéro):
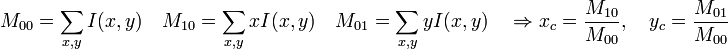
- centrer W sur le barycentre (xc,yc).
Camshift couplé: cas des séquences d'images
| DetectionVisage Ilkay.gif Initialisation de la cible | SkinColorModel ilkay.gif Modélisation colorimétrique | CamshiftFaceTracking Ilkay.gif Poursuite de la cible |
Le Camshift couplé adapte le Camshift au suivi d'objet : le mean shift est appliqué à l'image, avec une taille de fenêtre fixe et jusqu'à convergence, puis la taille de W est modifiée pour l'image suivante. Les nouvelles dimensions de W sont définies à partir de l'ellipse déduite des moments centraux du second ordre de la distribution spatiale de la teinte chair, calculés sur la fenêtre produite par le mean shift augmentée de
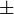
- Calculer la distribution de probabilité sur une région de recherche plus grande que la fenêtre initiale du mean shift.
- Initialiser la fenêtre W du mean shift.
- Appliquer le mean shift jusqu'à convergence : soit Wf la fenêtre obtenue.
- Augmenter la taille de Wf de
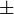
- Calculer le rectangle initiale du mean shift pour l'image suivante, et l'agrandir de
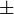
- Ré-itérer les étapes précédente pour l'image suivante.
Estimation des paramètres de l'ellipse à partir des moments du second ordre de la distribution de probabilité I = Pskin de couleur peau. Lorsque le mean shift arrive a convergence, le Camshift agrandit la fenêtre W et calcule l'ellipse de confiance à 99% des points qu'elle contient. On suppose en effet que ces points ont une distribution 2D Gaussienne, ce qui permet d'estimer les paramètres de cette ellipse à partir des moments du second ordre de la région d'intérêt W.
Le moment central d'ordre i pour et j pour y est définie par :
| μi,j = | ∑ | (x − xc)i(y − yc)jI(x,y) |
| x,y |
la sommation ayant lieu sur la fenêtre agrandie. L'orientation de l'ellipse est donnée par θ:
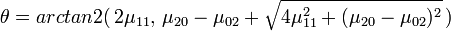
où la fonction arctan2 est la tangente inverse à quatre quadrants. On évalue alors les moments d'inertie principaux de l'ellipse, définis par :
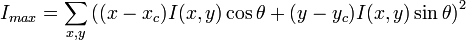
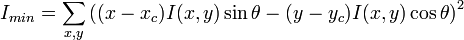
soit :
d'où l'on déduit les dimensions du grand axe a et du petit axe b de l'ellipse :
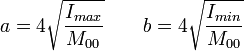
Si a < b, ce qui a lieu lorsque l'ellipse fait un angle supérieur à 45° avec l'horizontale, ces longueurs sont permutées, et l'angle θ est pris égale à π / 2 − θ.
La hauteur et la largeur de la fenêtre initiale du mean shift pour la prochaine image sont alors déduites par projection des sommets de l'ellipse sur les axes x et y :

Cette fenêtre sert à initialiser la recherche du maximum de la probabilité de la couleur peau, mais le Camshift couplé précise aussi que cette probabilité doit être calculée sur un voisinage plus étendu de cette fenêtre : p(peau | x,y) est calculée sur la fenêtre agrandie de