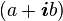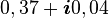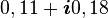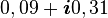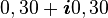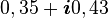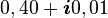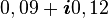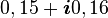Calculateur quantique - Définition

Simulation d’un calculateur quantique

Damian Conway a créé pour le langage Perl un module nommé Quantum::Superpositions qui permet de simuler (en faisant de l’algorithmique ordinaire en coulisses, bien sûr) le fonctionnement d’un périphérique de calcul quantique. Ce module est utilisable pour écrire et tester, en version maquette à quelques qubits simulés, des programmes écrits pour la logique quantique. Les programmes réalisés seront intégralement utilisables sur un périphérique de calcul quantique (s’il en existe un jour) en remplaçant les appels au module par les appels correspondant à ce périphérique, sans toucher en rien au programme Perl lui-même excepté en ce qui concerne le nombre de qubits spécifié. On pourra alors tirer parti des capacités d’un calculateur quantique et effectuer ainsi des calculs plus complexes à temps égal.

Le module munit Perl de deux fonctions testant globalement les tableaux : any() et all(). Dans la simulation, ces fonctions travaillent par itération sur les éléments et donc en un temps O(N). Dans un calcul quantique, leur temps d’exécution serait indépendant de N.

L’expression d’un calcul de primalité :

      sub is_prime {                my ($n) = @_;                return $n % all(2..sqrt($n)+1) != 0              }      

n’est pas sans rappeler l’écriture en langage APL, qui lui aussi traite globalement les tableaux, ou d’un langage fonctionnel comme Haskell. Une extension de ce dernier nommé QHaskell (quantum Haskell) existe depuis 2006

Le MIT, pour sa part, a placé en Open source un outil d’aide à l’architecture de circuits quantiques (théoriques) simples.

Principe de fonctionnement des ordinateurs quantiques

Le fonctionnement des ordinateurs quantiques peut paraître mystérieux au premier abord : la théorie quantique est une théorie décrivant des probabilités de présence. Comment dès lors concilier ce concept d’aléa avec un calcul qui se veut déterministe ?

Idées de la mécanique quantique

En fait, les fonctions d’onde, c’est-à-dire les distributions de probabilité de présence à la base de la théorie quantique, sont issues de calculs tout ce qu’il y a de plus déterministes. La source d’aléa est dans l’acte d’observation lui-même, c’est-à-dire la mesure. En effet, suite à une mesure, le système quantique se fixe dans un état avec une certaine probabilité. On peut contourner cette incertitude en la rendant la plus faible possible par un jeu d’opérations quantiques successives. Pour certains algorithmes, il peut être nécessaire d’effectuer les calculs plusieurs fois jusqu’à ce que la réponse vérifie une certaine propriété.

En mécanique quantique, il est possible pour une particule d’être dans de multiples états simultanément. Cette possibilité est appelée superposition. Pour décrire ce phénomène, on parle parfois du paradoxe du chat de Schrödinger qui est, pour l’observateur, à la fois mort et/ou vivant. Lorsque le chat dort, il est immobile, et l’on ne peut pas dire en le regardant s’il dort ou s’il est mort. Le chat peut donc être dans deux états différents que l’on ne peut différencier uniquement par l’observation.

• L’observateur qui veut étudier avec une certitude absolue l’état de mort du chat ne pourra s’assurer qu’il est bien mort qu’en essayant de le réveiller. Si le chat est bien mort, le chat ne se réveille pas, donc ne change pas de position, donc l’état n’est pas perturbé, et l’on peut étudier cet état de mort du chat en étant certain que le chat que l’on observe est bel et bien mort.
• Mais l’observateur qui veut étudier avec une certitude absolue l’état de sommeil du chat ne pourra s’assurer de cet état qu’en réveillant le chat. C’est ici qu’est le paradoxe : en réveillant le chat, l’observateur altère l’état qu’il voulait étudier, et il ne peut donc plus l’étudier. L’astuce consiste donc à supposer que le chat est endormi (probabilité = 50% = 1 chance sur 2), à l’observer d’abord, puis à vérifier ensuite en essayant de le réveiller. On ne conserve les résultats de l’observation que si le chat se réveille.
• Avec seulement deux états possibles, le raisonnement est simple. Tout se complique si l’on considère qu’il y a plusieurs chats à étudier en même temps et qu’il y a trois états possibles, c’est-à-dire que chaque chat peut être soit mort, soit endormi, ou bien les deux états à la fois en superposition (ce qui est possible pour une particule isolée).

Cependant au niveau quantique, il ne s’agit pas seulement d’un modèle permettant de rendre compte de notre ignorance du système. Les particules sont véritablement dans cet état superposé, et il en découle un certain nombre de propriétés inédites à notre échelle. Une mesure sur un système quantique va le forcer à choisir un des états. On parle de projection.

Le qubit

La mémoire d’un ordinateur classique est faite de bits. Chaque bit porte soit un 1 soit un 0. La machine calcule en manipulant ces bits. Un ordinateur quantique travaille sur un jeu de qubits. Un qubit peut porter soit un un, soit un zéro, soit une superposition d’un un et d’un zéro (ou, plus exactement, il porte une distribution de phase, angle qui pour 0° lui fait prendre la valeur 1, pour 90° la valeur 0, et entre les deux la superposition d’états dans les proportions du sin² et du cos² de la phase). L’ordinateur quantique calcule en manipulant ces distributions. On n’a donc pas trois états en tout mais une infinité.

De plus, l’état de plusieurs qubits réunis n’est pas seulement une combinaison des états respectifs des qubits. En effet, si un qubit est dans une quelconque superposition d’états , deux qubits réunis sont quant à eux dans une superposition d’états , avec | α | ² + | β | ² + | γ | ² + | δ | ² = 1. Il s’agit cette fois d’employer la superposition des quatre états pour le calcul. C’est pourquoi la puissance de calcul théorique d’un ordinateur quantique double à chaque fois qu’on lui adjoint un qubit. Avec 10 qubits, on a 1024 états superposables, et avec n qubits, 2ⁿ.

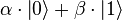
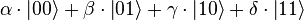
Un ordinateur classique ayant trois bits de mémoire peut stocker uniquement trois nombres binaires. À un moment donné, il pourrait contenir les bits « 101 » ou une autre combinaison des 8 possibles (2³). Un ordinateur quantique ayant trois qubits peut en fait stocker 16 valeurs, assemblées deux par deux pour former 8 nombres complexes (il est donc dans une superposition de ces 8 états). Il pourrait contenir ceci :

État	Amplitude	Probabilité
		(a2 + b2)
000		0,14
001		0,04
010		0,10
011		0,18
100		0,31
101		0,16
110		0,02
111		0,05

Noter que la somme des probabilités fait bien 1. S’il y avait eu n qubits, cette table aurait eu 2ⁿ lignes. Pour un n aux alentours de 300, il y aurait eu plus de lignes que d’atomes dans l’univers observable.

La première colonne montre tous les états possibles pour trois bits. Un ordinateur classique peut seulement porter un de ces états à la fois. Un ordinateur quantique, lui, peut être dans une superposition de ces 8 états à la fois. La deuxième colonne montre l’amplitude pour chacun des 8 états. Ces 8 nombres complexes sont un instantané du contenu d’un ordinateur quantique à un moment donné. Durant le calcul, ces trois nombres changeront et interagiront les uns avec les autres. En ce sens, un ordinateur quantique à trois qubits a bien plus de mémoire qu’un ordinateur classique à trois bits.

Cependant, il n’est pas possible de voir directement ces trois nombres. Quand l’algorithme est fini, une seule mesure est accomplie. La mesure retourne une simple chaîne de 3 bits classiques et efface les 8 nombres quantiques. La chaîne de retour est générée aléatoirement. La troisième colonne donne la probabilité pour chacune des chaînes possibles. Dans cet exemple, il y a 14% de chance que la chaîne retournée soit « 000 », 4% que ce soit « 001 », ainsi de suite. Chaque nombre complexe est nommé « ampere » et chaque probabilité une « amplitude carrée », parce qu’elle est égale à a² + b². La somme des huit probabilités est égale à un.

Typiquement, un algorithme d’un ordinateur quantique initialisera tous les nombres complexes à des valeurs égales, donc tous les états auront les mêmes probabilités. La liste des nombres complexes peut être imaginée comme un vecteur à 8 éléments. À chaque étape de l’algorithme, le vecteur est modifié par son produit avec une matrice qui correspond à une opération quantique.

Technologies

Un article publié en avril 2008 par Scientific American fait état d’une avancée vers le calculateur quantique utilisant l’effet Hall quantique fractionnaire.