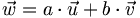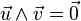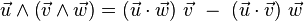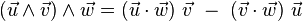Calcul vectoriel en géométrie euclidienne - Définition
La liste des auteurs de cet article est disponible ici.
Produit mixte
Définition et propriétés
Étant donnés trois vecteurs
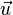
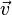
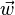
-
![\left[\vec u, \vec v, \vec w\right] = (\vec u \wedge \vec v) \cdot \vec w\,](https://static.techno-science.net/illustration/Definitions/autres/e/e3e94bd42adeb89556d444a062b694c4_235383d7f0e8425cce4294ee0e759328.png)
On peut démontrer que l'on a :
et
et aussi :
![\left[\vec u, \vec v, \vec w\right] = \begin{vmatrix} u_x & u_y & u_z\\v_x & v_y & v_z\\w_x & w_y & w_z \end{vmatrix}](https://static.techno-science.net/illustration/Definitions/autres/4/4f9e150129fca86f8f9a817603d4a6a4_5a74aa3c8539ecc1c1ca4553313e3eba.png)
autrement dit :
![\left[\vec u, \vec v, \vec w\right] = (u_x v_y w_z + v_x w_y u_z + w_x u_y v_z) - (u_z v_y w_x + v_x w_z u_y + w_y u_x v_z)\,](https://static.techno-science.net/illustration/Definitions/autres/5/56b2d64ea817a9f73e683384852d4384_d4fb9b5be6ba29cc068bf91960805f26.png)
Remarques :
- Si deux des trois vecteurs sont égaux ou colinéaires, le produit mixte est nul.
- Le produit mixte de trois vecteurs vrais (en opposition à des pseudovecteurs) est une quantité pseudoscalaire.
Application du produit mixte
- Si les vecteurs
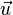
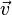
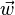
![\left[\vec u, \vec v, \vec w\right]\,](https://static.techno-science.net/illustration/Definitions/autres/b/b03580ab9cbe8ad1222dfafc855ee3e4_f7f650bad999beb41e90d3bf339d2018.png)
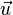
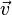
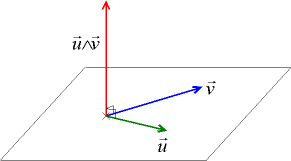
Produit vectoriel de deux vecteurs dans l'espace
Notons tout d'abord que deux vecteurs non colinéaires


Trois vecteurs non coplanaires forment une base. La base


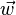
On définit le produit vectoriel des deux vecteurs


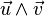
- normal au plan vectoriel de base
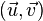
- dont la norme vaut
- tel que
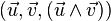
On étend la définition précédente au cas où


- Remarque
Le produit vectoriel agit sur des objets mathématiques de différentes sortes, soit des vecteurs, soit des pseudovecteurs. Cette distinction est peu importante en base orthonormée (sauf pour les symétries), mais si elle n'est pas faite en base non orthonormée, cela aboutit à des absurdités. On a ce problème en physique avec notamment les champs magnétiques et les moments, qui ressemblent beaucoup aux vecteurs, mais qui sont en fait des pseudovecteurs, et n'obéissent pas aux mêmes règles de calcul.
Double produit vectoriel
On peut combiner trois vecteurs
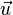
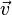
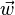
Exemple :
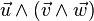
Comme le produit vectoriel n'est ni associatif, ni commutatif, il est nécessaire d'utiliser ici des parenthèses et le résultat va dépendre à la fois de l'ordre dans lequel les opérations sont effectuées et de l'ordre de présentation des 3 vecteurs.
On peut démontrer (sans difficulté mais assez laborieusement) les 2 formules suivantes :
et
Moyen mnémotechnique : le double produit vectoriel est forcément porté par les vecteurs entre parenthèses (puisque ne possède aucune composante sur le troisième vecteur) et le terme qui ne porte pas le signe

![\left[\vec u, \vec v, \vec w\right] = \left[\vec v, \vec w, \vec u\right] = \left[\vec w, \vec u, \vec v\right]\,](https://static.techno-science.net/illustration/Definitions/autres/2/2de66ecb34ed99f1843a1bff308ee501_499ad989a40717a0f8d093ab2c0966bc.png)
![\left[\vec v, \vec u, \vec w\right] = \left[\vec w, \vec v, \vec u\right] = \left[\vec u, \vec w, \vec v\right] = - \left[\vec u, \vec v, \vec w\right]\,](https://static.techno-science.net/illustration/Definitions/autres/d/d8d1d2a868d9c23b9695708d8f1c7989_d1f08d18d60c73a640bdaeec8753144e.png)