Calcul du volume de l'hypersphère - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La dérivation suivante pour le calcul du volume de l'hypersphère dépend des définitions précises de la sphère et de la boule. Le volume intérieur d'une sphère est le volume de la boule délimitée par la sphère.
Dérivation
Nous intégrerons en coordonnées cartésiennes orthonormales dans l'espace euclidien.
Formule générale (forme récursive)
Notons V(n)[r] le volume intérieur de l'hypersphère de rayon r et à n − 1 dimensions. Alors
- V(1)[r] = 2r
parce que c'est la longueur d'un segment deux fois plus long que le rayon, i.e.
-
![\{x\in\mathbb R:|x|\le r\}\qquad\text{ou}\qquad [-r,r]](https://static.techno-science.net/illustration/Definitions/autres/6/696edf6100e1e3b8442a2b4896cff456_7d114872c70d901175b0a8bf3e5ef05e.png)
La mesure de la sphère propre à dimension nulle est 2 parce que cette sphère consiste en deux points. Pour tout
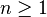
Le volume est proportionnel à la n:ième puissance du rayon
Nous montrerons premièrement par l'induction mathématique que le volume intérieur d'une hypersphère à n − 1 dimensions est proportionnel à la n:ième puissance de son rayon. Nous avons déjà observé que c'est vrai en dimension 1. Supposons maintenant que c'est vrai pour n dimensions, i.e.:
- V(n)[r] = rnV(n)[1].
Alors:
Maintenant nous avons établi que pour tout n≥1, le volume intérieur d'une hypersphère à n − 1 dimensions est proportionnel à la n:ième puissance de son rayon; c'est-à-dire que si nous notons le volume intérieur de l'hypersphère unitaire à n − 1 dimensions par V(n)[1], nous avons:
- V(n)[r] = rnV(n)[1],
-
![V^{(n+1)}[1] = V^{(n)}[1]\int_{-1}^1 \left(\sqrt{1-x^2}\,\right)^n dx.](https://static.techno-science.net/illustration/Definitions/autres/8/80e5acbb31b32d74a14463ac2bcd09e5_fa089afb19acba6e8ce7648cf690152f.png)
Deux ou trois dimensions
Dans le cas de V(2)[1] nous avons
qui est l'aire intérieure du cercle unité, ou, plus précisément, l'aire du disque borné par le cercle. La dérivation prochaine est très facile:
Ceci est le volume intérieur de la sphère unité, ou, plus précisément, le volume de la boule délimitée par la sphére.
Cas général
Essayons maintenant de généraliser cette dérivation au cas de la boule à beaucoup de dimensions:
Voici un graphe de la fonction que nous avons intégrée ici, pour rendre plus facile la visualisation de cette fonction dans plusieurs dimensions:
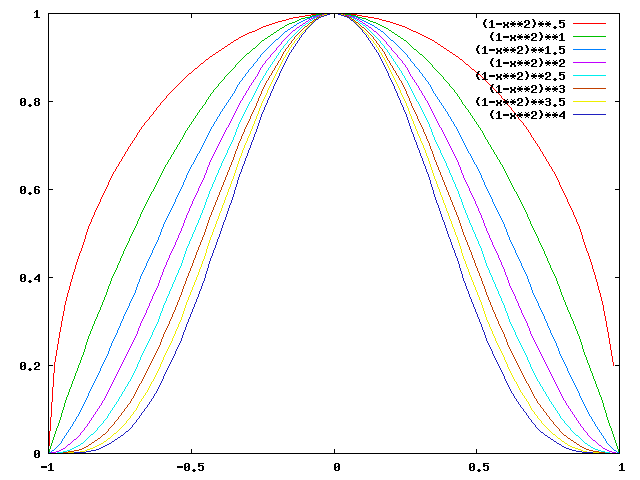
Comme vous pouvez voir, les hyperboules se pincent de plus en plus comme la dimension croît. (Plus précisément, puisque nous intégrons en coordonnées rectangulaires, et que les boîtes rectangulaires circonscrites aux boules s'étendent de plus en plus hors des boules comme la dimension croît, les boules nous paraissent de plus en plus pincées au point de vue des coordonnées dans lesquelles nous intégrons.)
Par le changement de variables u = 1 − x2 nous avons:
L'intégrale à droite est connue comme la fonction bêta:
qui peut être exprimée au moyen de la fonction gamma:
À partir de la relation
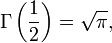
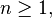
Forme générale et l'aire de la surface
L'aire de la surface de l'hypersphère, i.e. la mesure du volume de l'hypersphère propre, est la dérivée du volume de la boule (à une dimension de plus) délimitée par elle, par rapport à son rayon. Si le volume de la boule à n dimensions est
alors l'aire de la surface de la boule, c'est-à-dire le volume de l'hypersphère propre, (à une dimension de moins que la boule) est
Ceci s'appelle une désintégration de mesure, (d'après.)
![V^{(n+1)}[r] = \int_{-r}^r V^{(n)}\left[\sqrt{r^2-x^2}\,\right] dx.](https://static.techno-science.net/illustration/Definitions/autres/9/98b2a19b24d161b8a4588e4bd550d17f_490ea5cbe8d2f62bc6b4569f057663af.png)
![V^{(n+1)}[r] = \int_{-r}^r V^{(n)}\left[\sqrt{r^2-x^2}\,\right] dx,](https://static.techno-science.net/illustration/Definitions/autres/8/8b20d6e5e1f589c6b447f90749d7f583_01aa13e50f581e56551e619c955acc2a.png)
![V^{(n+1)}[r] = r \int_{-1}^1 V^{(n)}\left[\sqrt{r^2-(rx)^2}\,\right] dx,](https://static.techno-science.net/illustration/Definitions/autres/2/2d0a650dfa3874cbad3d5d457f0b0ef9_9fedc5585a4c014bb8784bc542476a1e.png)
![V^{(n+1)}[r] = r \int_{-1}^1 V^{(n)}\left[r\sqrt{(1-x^2)}\,\right] dx,](https://static.techno-science.net/illustration/Definitions/autres/f/f06793e2856275fddfb9b4bb9f50dc62_48a5d38e39a3ca9be69666108f4dfab3.png)
![V^{(n+1)}[r] = r \int_{-1}^1 r^n V^{(n)}\left[\sqrt{(1-x^2)}\,\right] dx = r^{n+1}V^{(n+1)}[1].](https://static.techno-science.net/illustration/Definitions/autres/4/4f29fcbfdfe8c658b40ca5df8384aec8_0ecadd055234aa293b963082433fca9d.png)
![V^{(2)}[1] = V^{(1)}[1]\int_{-1}^1 \sqrt{1-x^2}\,dx = 2\left.\frac{x\sqrt{1-x^2}+\arcsin x} 2 \right|_{x=-1}^1 = \pi,](https://static.techno-science.net/illustration/Definitions/autres/e/e11cdfc848d219b518f18bd18113f2ec_bccfd4684e70b83758633aac0bd24c9c.png)
![V^{(3)}[1] = V^{(2)}[1] \int_{-1}^1 \left(1-x^2\right)dx = \frac 4 3 \pi.](https://static.techno-science.net/illustration/Definitions/autres/7/75a4aaa8505b9a1c102553a36c5ac017_96b95a7af46270330a7eb08c17a3f591.png)
![V^{(n+1)}[1] = V^{(n)}[1] \int_{-1}^1 \left(1-x^2\right)^{n/2} dx = V^{(n)}[1] \cdot 2\int_0^1 \left(1-x^2\right)^{n/2} dx.](https://static.techno-science.net/illustration/Definitions/autres/4/4d88b2b18b6bcbc25bd151dd38632397_01a1b6f085cbf1a2aa6099388e6b72e1.png)
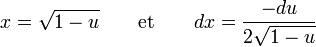
![V^{(n+1)}[1] = V^{(n)}[1] \cdot 2\int_0^1 \left(1-x^2\right)^{n/2} dx = V^{(n)}[1] \int_0^1 u^{n/2}(1-u)^{-1/2} du.](https://static.techno-science.net/illustration/Definitions/autres/5/50263e0d6f2c81429a9af9e7efa23b69_530753501d723d900ac1607b109ce94f.png)
![V^{(n+1)}[1] = V^{(n)}[1] \cdot\mathrm B\left(\frac n 2 + 1, \frac 1 2 \right),](https://static.techno-science.net/illustration/Definitions/autres/9/9c8c41af0791e32bc733a8d62622a001_21f91889a1a56acda029a36ef9684826.png)
![V^{(n+1)}[1] = V^{(n)}[1] \frac {\Gamma\left(\frac n 2 + 1\right)\Gamma\left( \frac 1 2 \right)} {\Gamma\left(\frac n 2 + \frac 3 2\right)}.](https://static.techno-science.net/illustration/Definitions/autres/c/cec8522c70e9b6777d21ab682a8dad46_cbbb078c90f1719ceab89c4168992c1f.png)
![V^{(n)}[1] = \frac {\pi^{n/2}}{\Gamma\left(\frac n 2 + 1 \right)}.](https://static.techno-science.net/illustration/Definitions/autres/1/1043a2c4a966e96b47dea92bb2a12cfb_c534957309f737a23b55819a5f265864.png)
![V^{(n)}[r] = \frac {\pi^{n/2} r^n}{\Gamma\left(\frac n 2 + 1 \right)},](https://static.techno-science.net/illustration/Definitions/autres/6/681f4f8f88532115c9ad30bce4cb9e86_07fd240d813c0ebfbd33e4639456e546.png)
![S^{(n-1)}[r] = \frac \partial{\partial r} V^{(n)}[r] = \frac {\pi^{n/2} nr^{n-1}}{\Gamma\left(\frac n 2 + 1 \right)} = \frac {2\pi^{n/2}r^{n-1}}{\Gamma\left( \frac n 2 \right)}.](https://static.techno-science.net/illustration/Definitions/autres/c/c2b64193c8e15664bfe5f3e8d2d5c101_9da27887027a007004970525d8c7370d.png)

















































