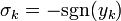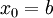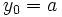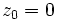CORDIC - Définition
La liste des auteurs de cet article est disponible ici.
Exemples de programmation
MATLAB
function v=cordic(beta,n) % Calcul de 'cos' et 'sin' d'un angle 'beta' (en radians) % par l'algorithme CORDIC. Résultat dans le vecteur 'v'. % 'n' est le nombre d'itérations (la précision augmente avec lui). %%Initialisation v=[1;0]; sigma=1; Kn=prod(1./sqrt(1+2.^(-2*(0:(n-1))))); %%Itérations for i=0:n-1; R=[1 -sigma*2^-i;sigma*2^-i 1]; v=R*v; beta=beta-sigma*atan(2^-i); sigma=sign(beta); end %% Calcul final v=v*Kn;
Langage C
Le code suivant utilise les flottants étendus (double). Beta est l'angle voulu en radians. On démarre par le vecteur v = (1;0), prémultiplié par K.
#include#include #include int main() { int nb_iter; // Nombre d'itérations double K = 0.6073; // Valeur de K double x = K, y = 0; // Valeur approchante de cos(beta) et sin(beta) double x_Nouveau; // Variable temporaire double beta = 0; // Angle à chercher printf("Calcul par la methode CORDIC de sinus: \n\n\n Veuillez entrer beta\n"); scanf("%lf",&beta); // entrer la valeur de beta printf("Veuillez entrer le nombre d'iterations voulues\n"); scanf("%ld",&nb_iter); // Entrer le nombre d'itération for(int i = 0; i < nb_iter; i++) { Pow2 = pow(2,-i); // Si beta<0 rotation dans le sens trigo if(beta < 0) { x_Nouveau = x + y*Pow2; y -= x*Pow2; beta += atan(Pow2); } // sinon dans l'autre sens else { x_Nouveau = x - y*Pow2; y += x*Pow2; beta -= atan(Pow2); } x = x_Nouveau; } printf("cos(beta) = %lf , sin(beta) = %lf \n", x,y); // Affichage du résultat return 0; }
Algorithme
En 1971, John Stephen Walther de Hewlett Packard, a présenté une généralisation de l'algorithme qui fut implémentée dans la calculatrice HP 35. Cette méthode permet de calculer notamment les fonctions hyperboliques mais également d'autres fonctions comme l'exponentielle, la division ou la multiplication. La généralisation se présente comme suit :
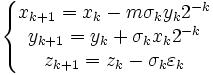
avec
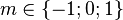
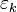
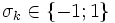
Fonctions trigonométriques
On utilise la généralisation avec les paramètres :
-
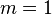
-
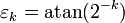
-
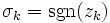
-
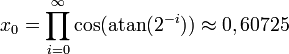
-
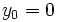
-
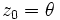
À la fin de n itérations, on a
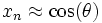
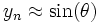
Cette méthode ne fonctionne que si :
En pratique cela ne pose pas de problème car les fonctions sinus et cosinus peuvent être extrapolées à partir des valeurs
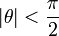
Fonctions hyperboliques
On utilise la généralisation avec les paramètres :
-
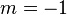
-
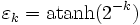
-
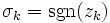
-
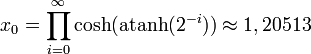
-
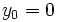
-
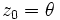
À la fin de n itérations, on a
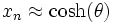
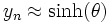
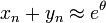
Cette méthode ne fonctionne que si la valeur absolue de z est inférieure à environ 1,05. Des transformations d'expressions grâce à des identités trigonométriques permettent de contourner ces problèmes en faisant en sorte que les paramètres soient dans l'intervalle requis. La répétition de certaines itérations résout les problèmes de convergence.
Fonctions linéaires
CORDIC permet également de calculer la multiplication ou la division entre des nombres a et b.
Multiplication
-
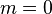
-
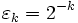
-
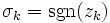
- x0 = a
-
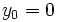
-
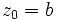
À la fin de n itérations, on a
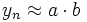
![b \in [-2;2]](https://static.techno-science.net/illustration/Definitions/autres/a/adf8f6796041affc80f0a6173dff414e_5e0b169add89e947a9720bf4f1bd5ee3.png)
Division
À la fin de n itérations, on a
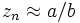
![b \in [-2;2]](https://static.techno-science.net/illustration/Definitions/autres/a/adf8f6796041affc80f0a6173dff414e_5e0b169add89e947a9720bf4f1bd5ee3.png)