Bruit blanc - Définition
La liste des auteurs de cet article est disponible ici.
Bruit blanc et simulations
Un bruit blanc de densité spectrale (voir analyse spectrale) S échantillonné au pas T contient des fréquences inférieures à 1/2T (voir Théorème de Shannon). C'est un bruit blanc filtré qui possède une variance finie. Celle-ci s'écrit, si la densité spectrale est exprimée sur une échelle en fréquences positives, σ = S/2T.
Un bruit blanc peut être engendré par une séquence de nombres au hasard qui correspond à une densité de probabilité uniforme sur un intervalle de largeur unité. Pour obtenir des nombres sur un intervalle de largeur a, il suffit de multiplier le résultat par a.
Conséquence du théorème de la limite centrale, le bruit blanc gaussien est particulièrement utile. Pour le créer, on peut utiliser la formule de Rice
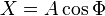
Φ est une séquence de variables uniformes sur un intervalle de largeur 2π.
A est une séquence de variables de Rayleigh dont la fonction de répartition s'écrit, σ2 étant la variance cherchée pour la variable de Gauss :
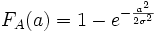
En égalant cette fonction de répartition à celle d'un nombre au hasard noté r, on obtient une réalisation de la variable de Rayleigh :
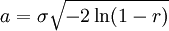
À partir de là, on construit une réalisation d'un bruit blanc gaussien. On peut alors obtenir une réalisation d'un processus gaussien quelconque en prenant sa transformée de Fourier, en la multipliant par la racine carrée de la densité spectrale et en inversant la transformée.

















































