Bissectrice - Définition
La liste des auteurs de cet article est disponible ici.
Bissectrices d'un triangle
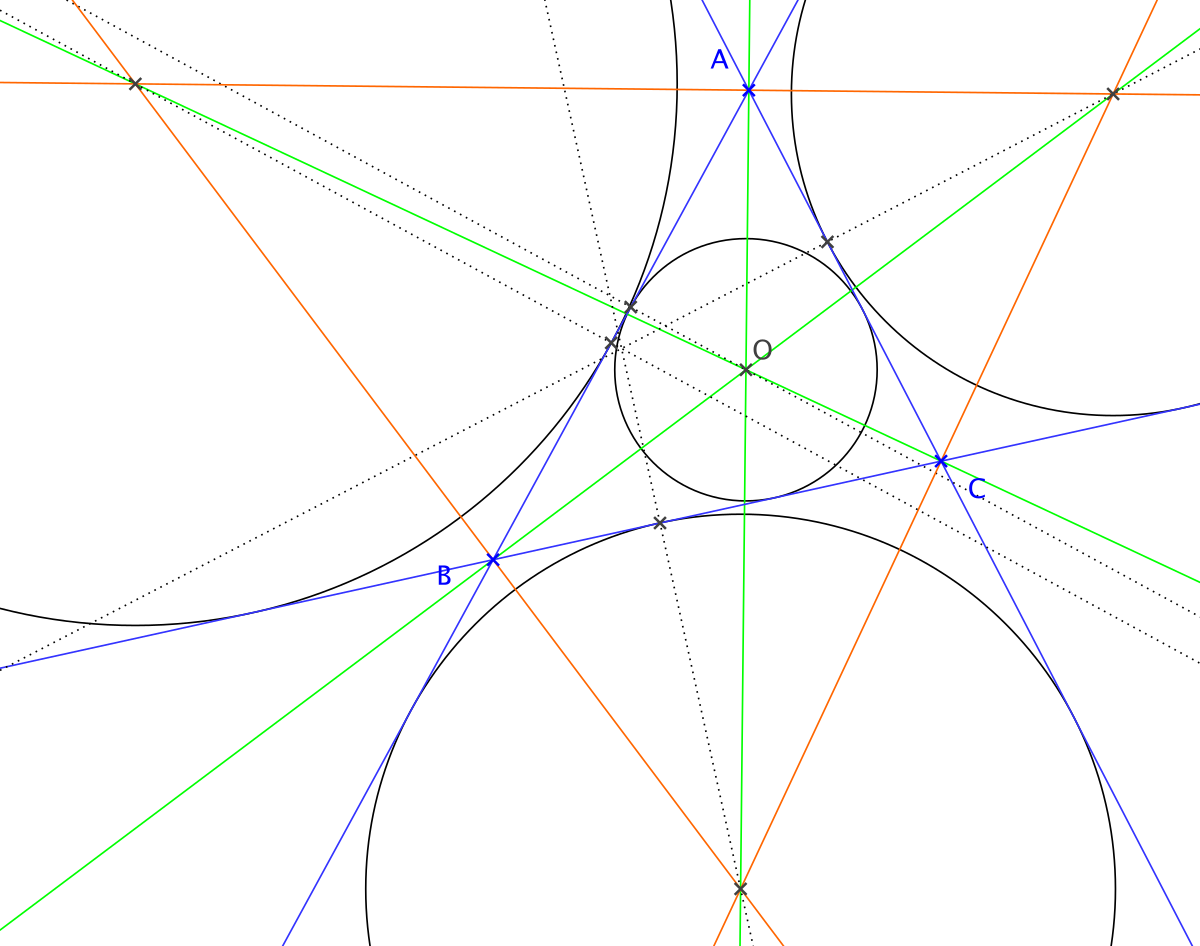
Cercles inscrit et exinscrits à un triangle — Dans un triangle,
- les bissectrices intérieures sont concourantes, leur point d'intersection étant le centre du cercle inscrit dans le triangle. Ce cercle est tangent aux trois côtés du triangle.
- Deux bissectrices extérieures concourent avec la bissectrice intérieure restante. On obtient ainsi les centres des trois cercles exinscrits au triangle.
Démonstration — Pour le premier point du théorème, le point d'intersection de deux bissectrices intérieures est à égale distance des trois côtés du triangle. Il est donc aussi sur la troisième bissectrice intérieure. Un cercle centré au point de concours et tangent à un côté sera tangent aux deux autres (appliquer le corollaire du théorème de la bissectrice (bis))
Théorème — Dans un triangle MAB avec I sur [AB], la droite (MI) est la bissectrice de l'angle en M si et seulement si MA/MB = IA/IB.
Une preuve par le théorème de Thalès est donnée dans la page sur les divisions harmoniques. Le calcul de deux manières des aires des triangles MAI et MBI donne une autre démonstration élémentaire.
Applications :
- On utilise extensivement la caractérisation précédente de la bissectrice dans l'étude du problème d'Apollonius : lieu des M tels que MA/MB = k.
- Avec cette caractérisation de la bissectrice, on retrouve aisément la bissectrice d'un angle MFN, où M et N sont deux points sur une ellipse (plus généralement, conique propre) de foyer F et de directrice D et la construction de la tangente en un point d'une conique.
Bissectrices de deux droites sécantes
Les bissectrices d'un couple de droites sécantes sont par définition les bissectrices des quatre secteurs angulaires définis par les deux droites. Il y a donc stricto sensu quatre bissectrices pour deux droites, si on s'en tient à la première définition de bissectrice. Au cours de la preuve du théorème suivant on montre que ces quatre bissectrices sont portées par deux droites qu'on appellera bissectrices des droites sécantes.
Théorème — Les bissectrices d'un couple de droites sécantes sont perpendiculaires.
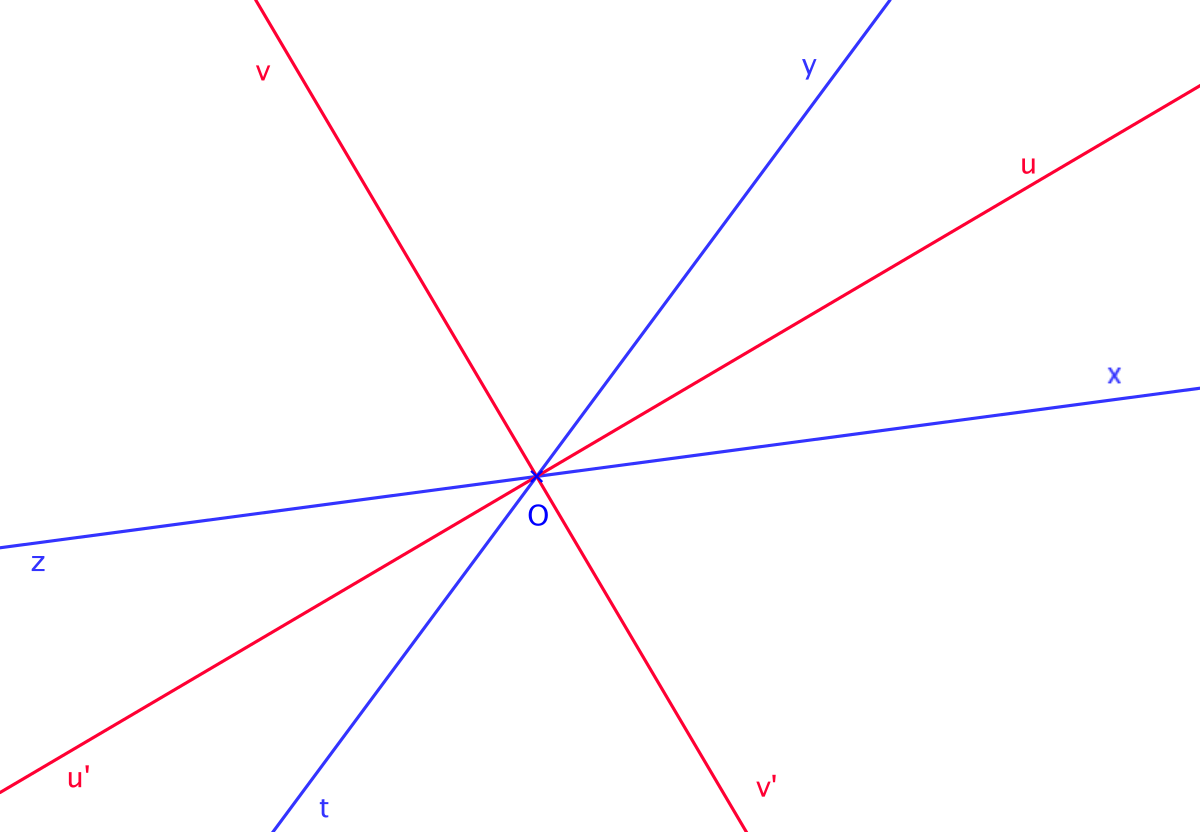
Notons (zx) et (ty) les deux droites. Elles se coupent en un point O. On appelle :
- [Ou) la bissectrice de xOy
- [Ou') la bissectrice de zOt
- [Ov) la bissectrice de yOz
- [Ov') la bissectrice de tOx
- Les angles xOy et zOt sont opposés par le sommet. Ils sont donc égaux. Les angles xOu = 1/2 xOy et zOu'=1/2 zOt sont donc aussi égaux. Comme [Ox) et [Oz) sont portées par une même droite il en va de même de [Ou) et [Ou') (on a aussi utilisé le fait que [Ou') est tracée dans le secteur zOt). Il en va de même pour les autres couples de bissectrices.
- Par hypothèse, les angles zOy et yOx sont supplémentaires : zOy + yOx = 180°. Donc uOv = uOy + yOv = 1/2 xOy + 1/2 yOz = 1/2 (xOy + yOz) = 180°/2 = 90°. CQFD
Bissectrices comme axes de symétrie de D u D'.— Si u et v sont deux vecteurs unitaires dirigeant respectivement D et D', alors u+v et u-v dirigent les axes de symétrie de la réunion D u D' (dessiner les losanges).
On obtient ainsi la notion de bissectrice de deux droites affines sécantes sans passer par le point de vue naïf des angles géométriques. Le produit scalaire (u+v).(u-v) est nul comme u et v sont unitaires : les deux bissectrices sont orthogonales.
Bissectrices de deux droites et faisceaux harmoniques —
- Si D et D' sont deux droites sécantes et

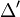

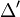
- Si D, D',