Axiomes de plans projectifs/Suite des axiomes - Définition

Introduction

La géométrie projective a permis de s'abstraire des impressions intuitives de la géométrie plane euclidienne. La géométrie projective ne travaille que sur les alignements et les intersections, elle ignore angles et longueurs. On part donc d'une base vraiment minimale à laquelle on ajoute des axiomes au compte-gouttes. Ainsi « tout univers possible dans l'imagination humaine » correspond à un ensemble d'axiomes qui définissent une structure d'Espace.

Les choses un peu compliquées commencent avec le théorème fondamental, les axiomes de Désargues et de Pappus, le théorème de Pascal ; tous ces concepts permettent de travailler sur des objets composites tels que les tripoints, tridroites, quadripoints, hexagrammes magiques pour aboutir à une théorie projective unifiée des coniques, théorie qui n'a pas besoin d'employer les notions de distance (point-point ou point-droite).

Cascade d'axiomes de plans projectifs

Plan projectif-tout-court

Un plan projectif (PP) est un ensemble de points et de droites (c'est-à-dire de groupements de points qu'on appellera droites). Un point est incident à cette droite s’il appartient à ce groupement. Une droite est incidente à un point si ce point fait partie de ce groupement. On dit aussi que cette droite passe par ce point ou que ce point est sur cette droite. Ce ne sont là que des questions de vocabulaire. Attention, une droite ne ressemble pas forcément aux droites du plan euclidien « naturel », ce n'est qu'un mot pour désigner des sous-ensembles de points.

Pour mémoire : plan projectif d'incidence (la base minimaliste)

Pour mémoire : plan projectif homogène (et barycentrique)

En dehors des PPH et de la démonstration du théorème fondamental -voir infra- on peut s'efforcer de raisonner sans aucune utilisation de coordonnées quelles qu'elles soient.

Plan projectif fondamental

Un plan projectif fondamental (PPF) est un PPI qui vérifie l’axiome fondamental de la géométrie projective, donc au total les axiomes :

1. Il existe au moins 2 points.
2. Chaque droite possède au moins 3 points.
3. Pour deux points distincts il existe une et une seule droite qui leur est incidente.
4. Deux droites distinctes ont un et un seul point commun.
5. Pour toute droite il existe au moins un point non incident à cette droite.
6. Axiome fondamental : une transformation projective unidimensionnelle d'une droite sur elle-même qui comporte trois points fixes est l'identité projective unidimensionnelle.

Plan projectif de Pappus

Un plan projectif de Pappus (PPP) est un PPI qui vérifie l’axiome de Pappus, donc au total :

1. Il existe au moins 2 points.
2. Chaque droite possède au moins 3 points.
3. Pour deux points distincts il existe une et une seule droite qui leur est incidente.
4. Deux droites distinctes ont un et un seul point commun.
5. Pour toute droite il existe au moins un point non incident à cette droite.
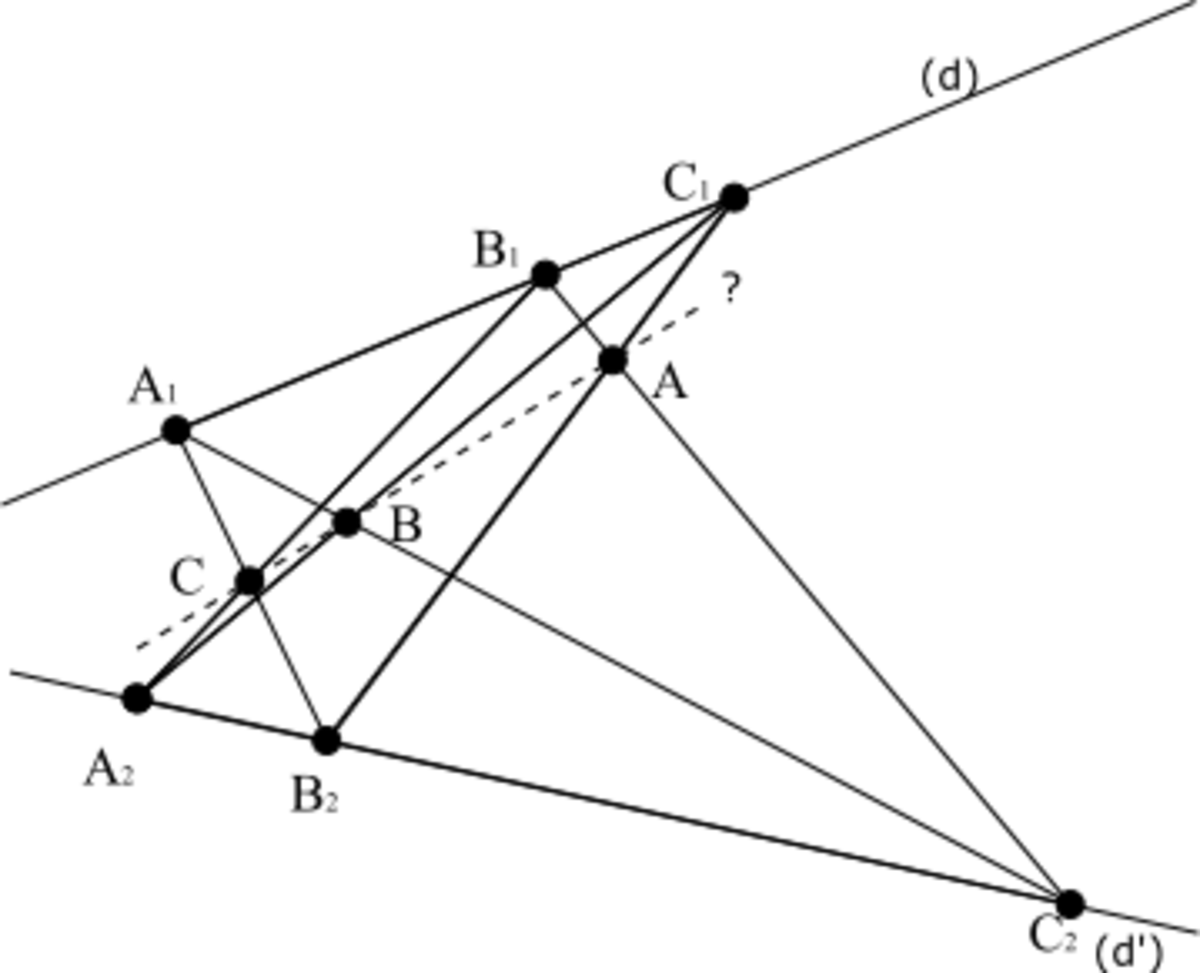
6. Axiome de Pappus-projectif : Si les points A1,B1,C1 sont alignés et si les points A2,B2,C2 sont alignés alors les intersections A B C sont aussi alignées. - -

On remarque que cette figure est autoduale.

Coloriage

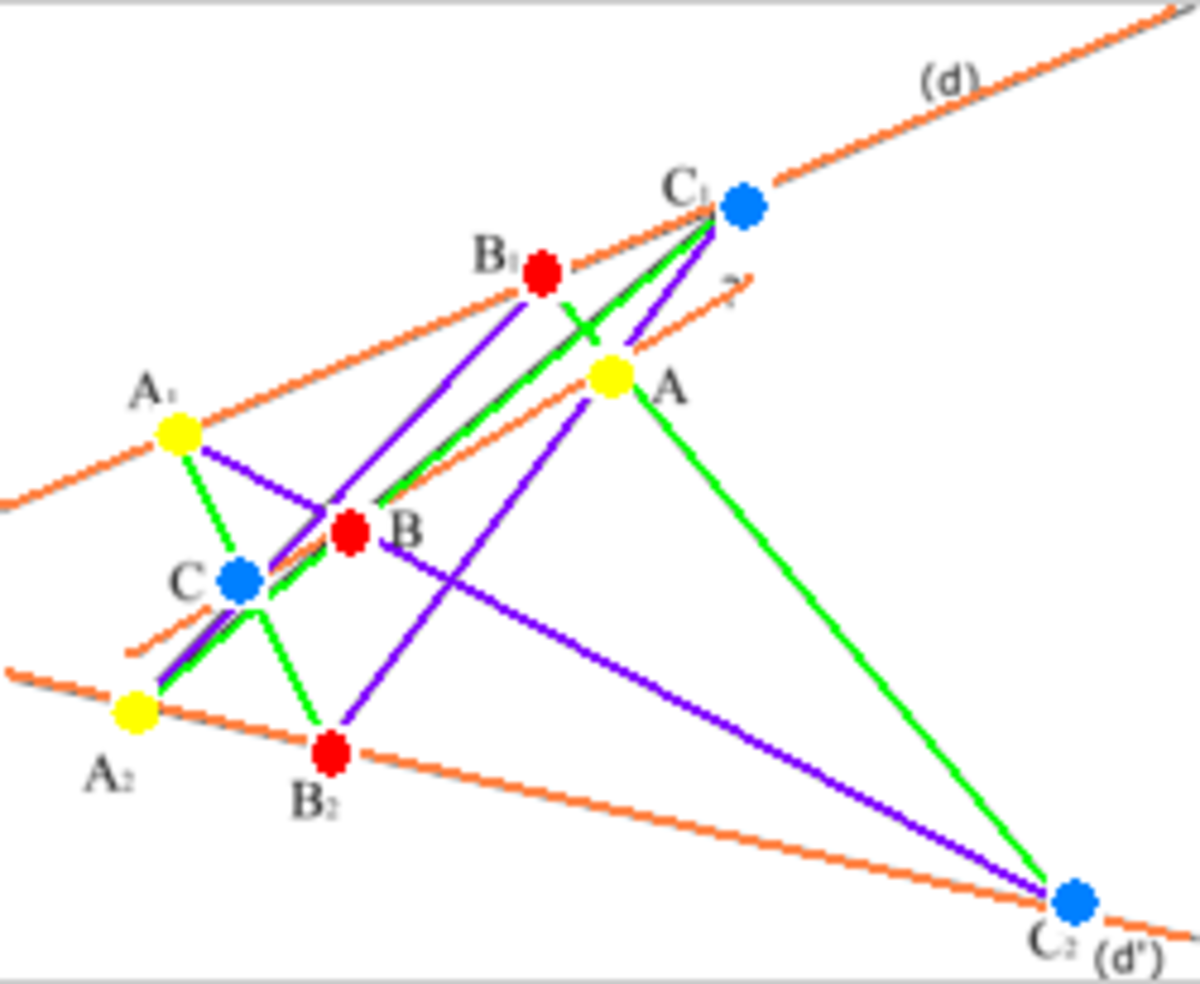
La configuration de Pappus possède une intéressante propriété de coloriage des 9 points et des 9 droites. On peut colorier les points avec 3 couleurs, deux points d'une même couleur n'étant jamais sur une droite de la configuration, sur chaque droite on trouve les trois couleurs de points. Dualement, on peut colorier les droites avec 3 couleurs, deux droites d'une même couleur ne se croisant jamais sur un point de la configuration, en chaque point on trouve les trois couleurs de droites. Les points bleus sont C1 C C2, les points rouges sont B1 B B2, les points jaunes sont A1 A A2. Les droites sont coloriées en violet, vert, orange. Dans ce cas particulier, les droites-supports sont orange, l'hexagramme-hexagone est vert-violet-vert-violet-vert-violet ; si on se place du point de vue des sommets, l'« hexangle » est bleu-rouge-jaune-bleu-rouge-jaune.

Plan projectif de Désargues-ou arguésien

Définition d'un plan projectif de Désargues-ou arguésien

Un plan projectif arguésien (PPA) est un PPI qui vérifie l’axiome de Désargues, donc au total :

1. Il existe au moins 2 points.
2. Chaque droite possède au moins 3 points.
3. Pour deux points distincts il existe une et une seule droite qui leur est incidente.
4. Deux droites distinctes ont un et un seul point commun.
5. Pour toute droite il existe au moins un point non incident à cette droite.
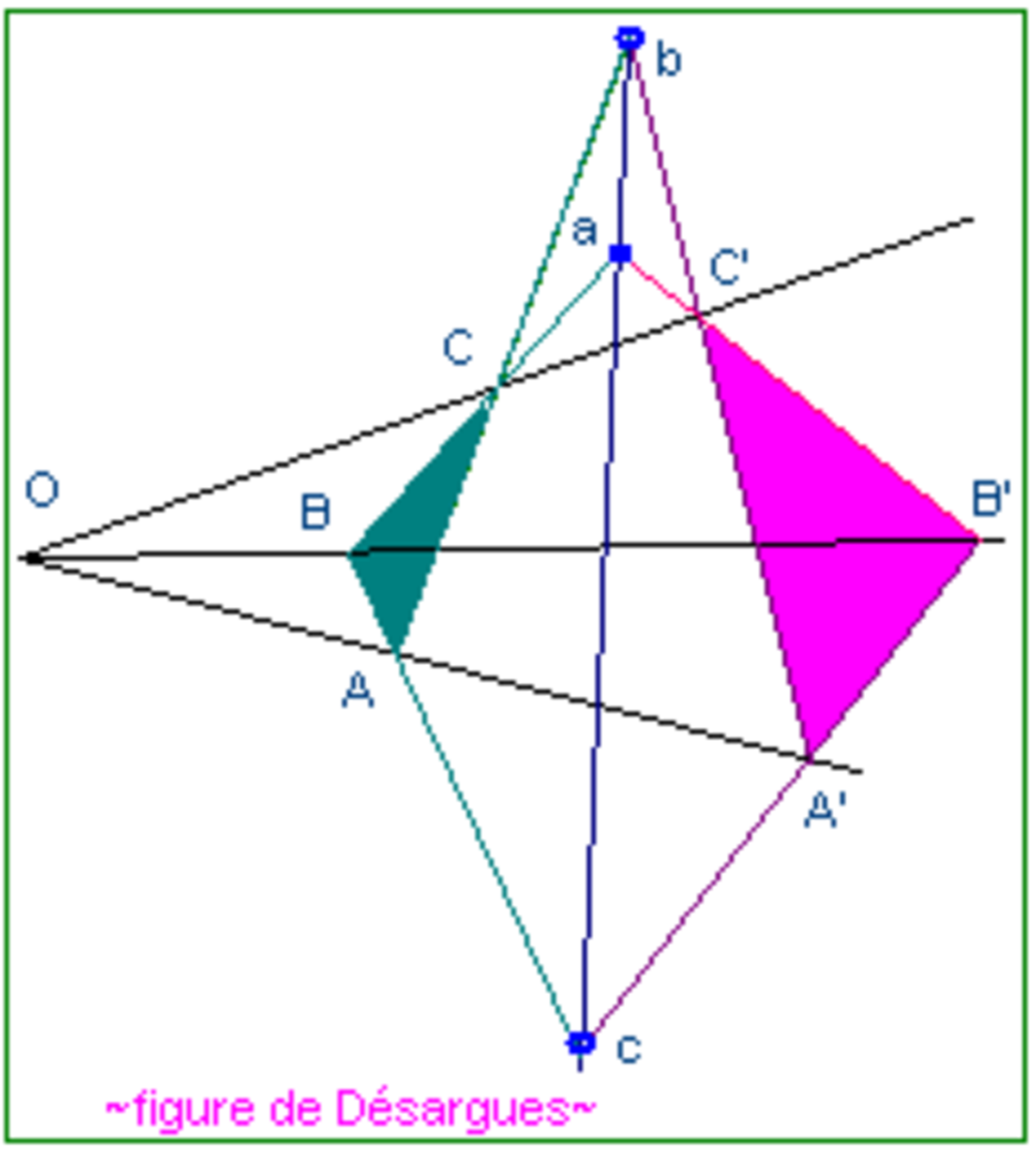
6. Axiome de Désargues : Étant donnés deux triangles ABC et A'B'C', si AA', BB' et CC' sont concourantes alors les 3 points d'intersection a, b et c des côtés homologues sont alignés.

Harmonie dans un plan projectif arguésien

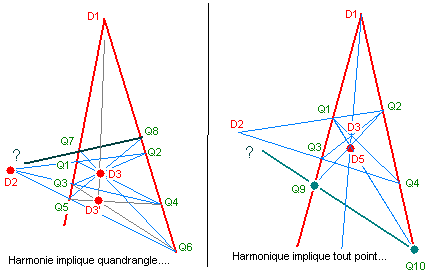Concernant les quadruplets harmoniques, l'axiome de Désargues permet de prouver au moins deux théorèmes.

Si un quadruplet est harmonique, alors il existe au moins un autre quadrangle complet qui correspond à ce quadruplet. (figure de gauche)- Soit le quadrangle Q1 Q2 Q3 Q4 qui serte à définir le quadruplet harmonique {Q1Q3, Q2Q4, D2, D3}. Nous pouvons construire un autre quadrangle complet ayant la même propriété en traçant la droite arbitraire Q5Q6 qui passe par D2 puis l'intersection D3' des droites Q3Q6 et Q4Q5, puis les intersections Q7 et Q8. La démonstration emploie 2 fois de suite l'axiome de Désargues. Dans les triangles D3Q1Q2 et D3'Q5Q6 les intersections D2, Q3, Q4 sont alignées, donc d'après le dual de Désargues les rayons D3D3', Q1Q5 et Q2Q6 sont concourants, donc D1 D3 D3' sont alignés. Ensuite, les triangles Q3Q4D3' et Q7Q8D3 sont en situation perspective arguésienne, par conséquent les côtés homologues ont leurs intersections alignées : Q5Q6 et Q7Q8 se coupent en D2. Par conséquent le quadrangle Q5Q6Q7Q8 a 2 points diagonaux D2 et D3 qui sont harmoniques avec 2 côtés Q1Q3 et Q2Q4, ce qui est bien le quadruplet du début.

Le deuxième théorème, figure de droite, s'énonce ainsi : Soit un quadruplet harmonique {Q1Q3, Q2Q4, D2, D3} et D5 un point quelconque sauf D1 de la droite D3D1. Alors le quadruplet {Q1Q3, Q2Q4, D2, D3} est lui aussi harmonique. La démonstration se fait en appliquant l'axiome de Désargues aux triangles Q3Q4D3 et Q9Q10D5. Ce théorème est très utile, il exprime que dans un quadruplet harmonique on peut faire coulisser chacun des points sur la droite qui le joint au sommet de la bidroite.

Lien entre les figures de Ceva et de Menelaus dans un plan projectif arguésien

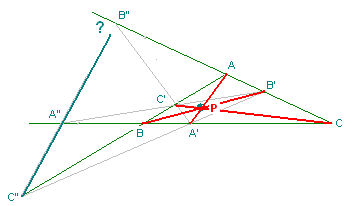
Soit un triangle ABC, un point P non situé sur un côté du triangle ; les droites AP, BP, CP s'appellent céviennes du point P, les intersections A' B' C' s'appellent les pieds des céviennes de P, du nom de Giovanni Ceva (1647-1734) ; le quadrangle complet C' B' B C permet de mettre en évidence le conjugué harmonique A", idem pour B" et C". Or les triangles ABC et A'B'C' sont en perspective arguésienne, donc les points A"B"C" sont alignés sur une droite que l'on appelle ménélienne, du nom de Ménélaüs d'Alexandrie (Ier siècle). D'où le théorème à la formulation moins élégante que la figure : Dans un triangle, les points conjugués harmoniques des pieds des céviennes, points situés sur les côtés du triangle, sont alignés sur une ménélienne.

Les axiomes invisibles

Les axiomes supposés connus sont ceux de la théorie des ensembles, ceux des nombres entiers, ne serait-ce que pour dire que toute droite comporte au moins 3 points distincts. Il y a aussi les axiomes et les règles de la logique mathématique qui sont utilisés dans toute démonstration. Un dernier axiome implicite que l'on pourrait qualifier « axiome d'abondance », est que le plan projectif comporte toujours suffisamment de points distincts pour que la figure ne soit pas dégénérée (pour une étude très rigoureuse, lire les fondements de la géométrie, 1985, Jacqueline Lelong-Ferrand). Par exemple pour l'axiome de Pappus le plan comporte au moins 9 points et 9 droites. Si on voulait être plus stricts, et ce serait fastidieux, on devrait, lors de la définition du point d'intersection entre deux droites, distinguer le cas où ce point est vraiment nouveau et le cas où ce point est déjà connu parmi les points précédents de la figure. Cette question est illustrée avec le Plan Projectif d'Incidence de Fano : il comporte 7 droites et 7 points, chacun ne contenant que 3 éléments ; comment y exhiber une configuration de Pappus ?