Axiomes de Hilbert - Définition

La représentation d'Euclide

Angles et longueurs chez Euclide

Preuve d'Euclide

Pour une image fixe, cliquer sur la flèche

Pour une animation, cliquer sur la flèche

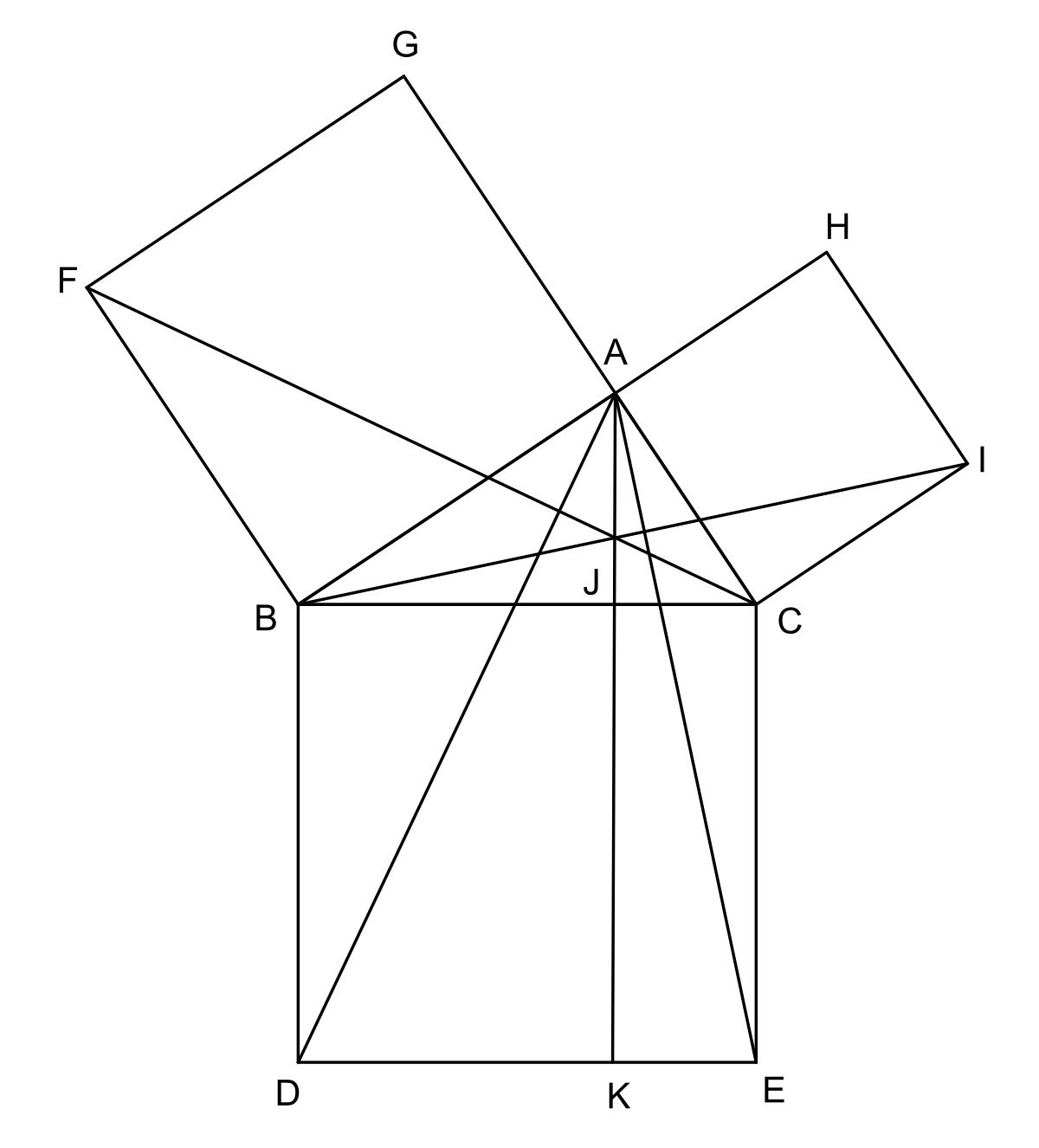
Euclide définit dans sa géométrie les notions de longueur et d'angle. Il est intéressant de voir ce qu'Euclide présuppose implicitement lorsqu'il les utilise.

Les définitions d'angle, d'angle droit, d'angle obtus, d'angle aigu, apparaissent dès les premières définitions du Livre I des Éléments.

Un angle plan est l'inclinaison mutuelle de deux lignes qui se touchent dans un plan, et qui ne sont point placées dans la même direction.

Lorsque les lignes, qui comprennent ledit angle, sont des droites, l'angle se nomme rectiligne.

Lorsqu'une droite tombant sur une droite fait deux angles de suite égaux entre eux, chacun des angles égaux est droit.

L'angle obtus est celui qui est plus grand qu'un droit.

L'angle aigu est celui qui est plus petit qu'un droit.

Cependant Euclide ne précise pas comment il définit l'égalité ou la comparaison de deux angles, pas plus qu'il ne définit l'égalité de deux longueurs. En fait, il apparaît qu'Euclide utilise implicitement la conservation des angles ou des longueurs de segments lorsque ceux-ci sont déplacés d'une position à l'autre, même si la notion de déplacement n'apparaît pas non plus explicitement dans les Éléments. Ainsi, pour montrer qu'un triangle ABC, ayant deux côtés AB et AC de même longueur, est tel que les angles B et C sont égaux, Euclide superpose les triangles ABC et ACB. Il suppose donc implicitement que, dans cette superposition, longueurs et angles sont conservés. La géométrie d'Euclide est donc ce qu'on pourrait appeler une géométrie des figures rigides.

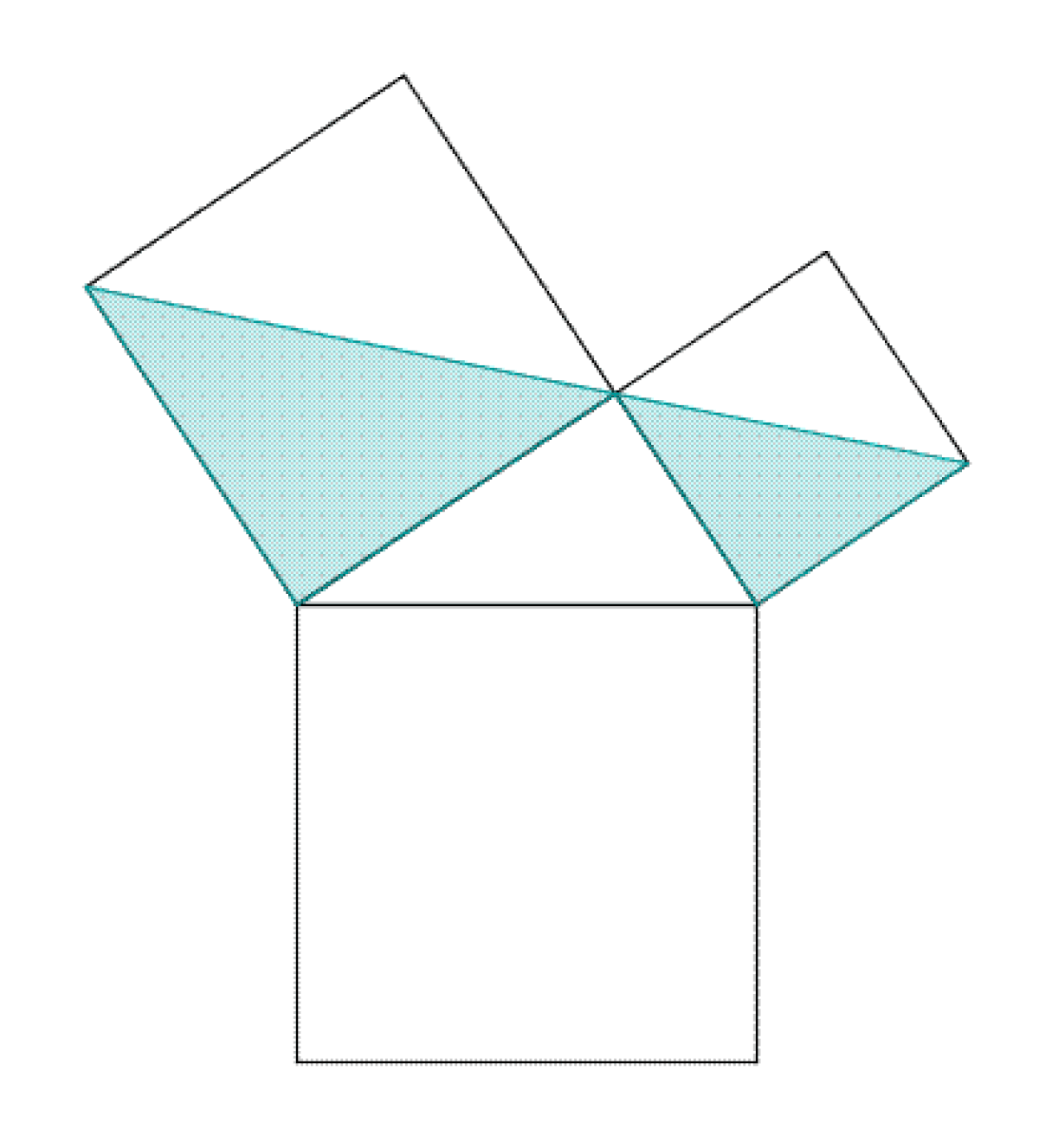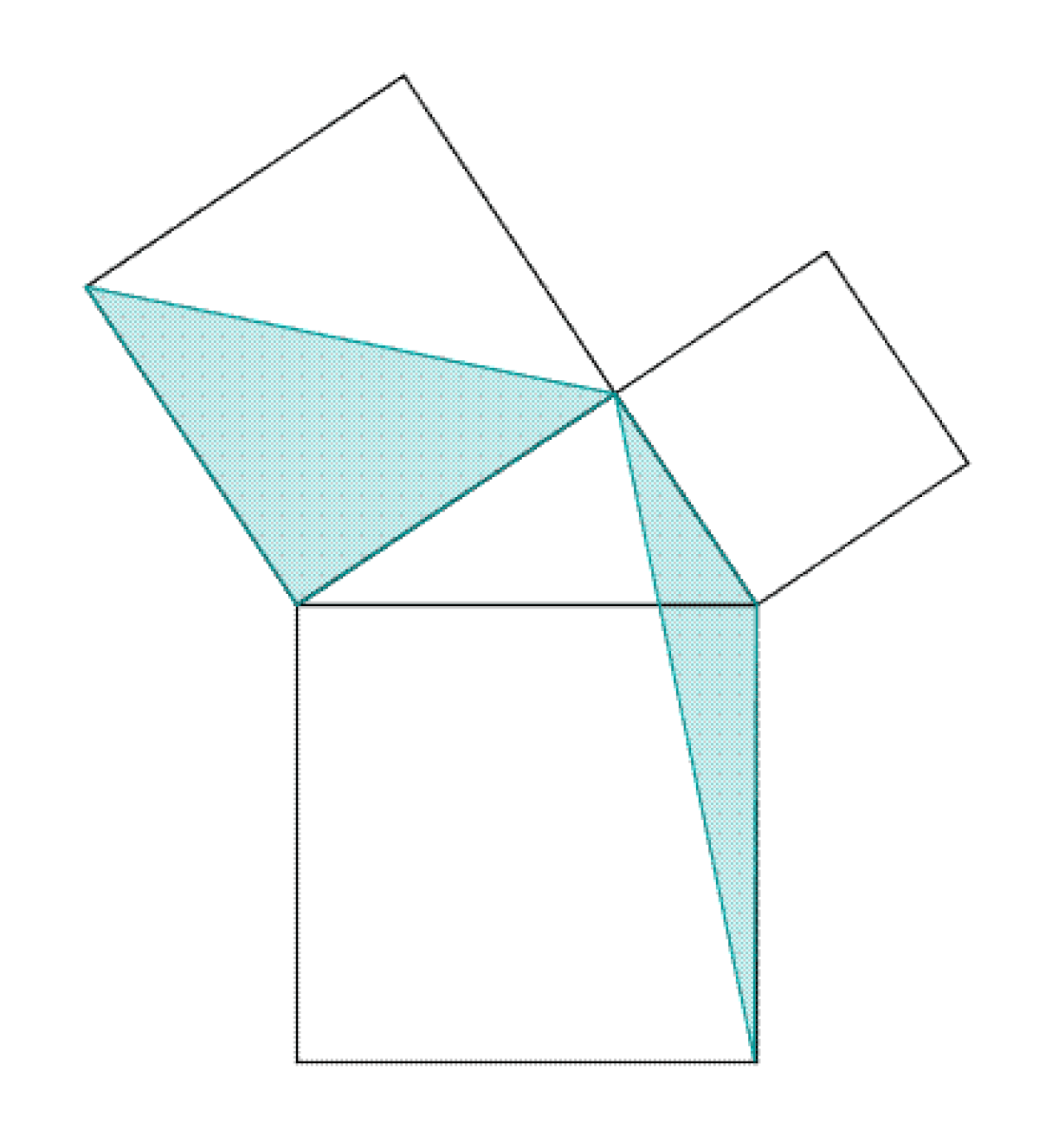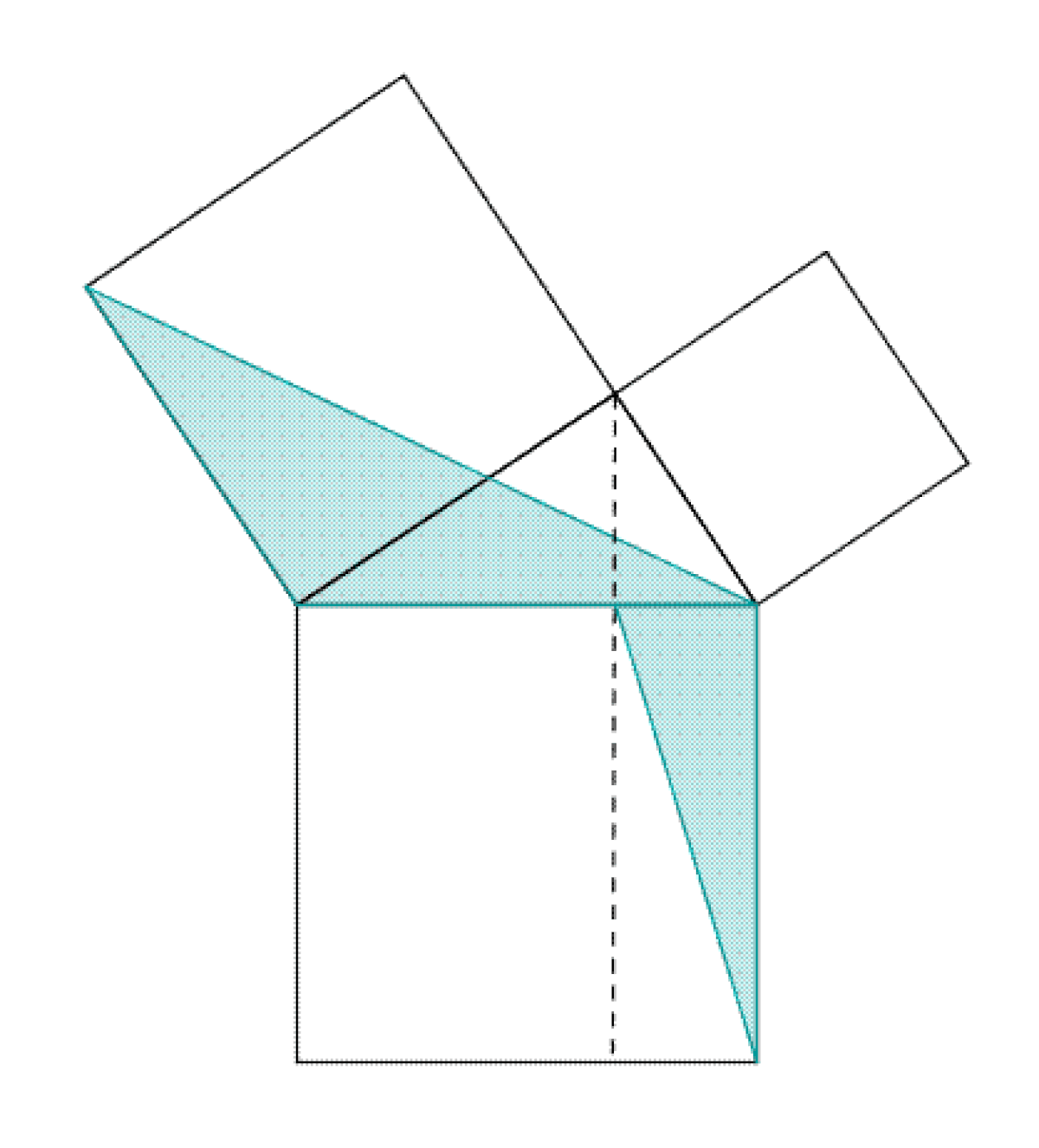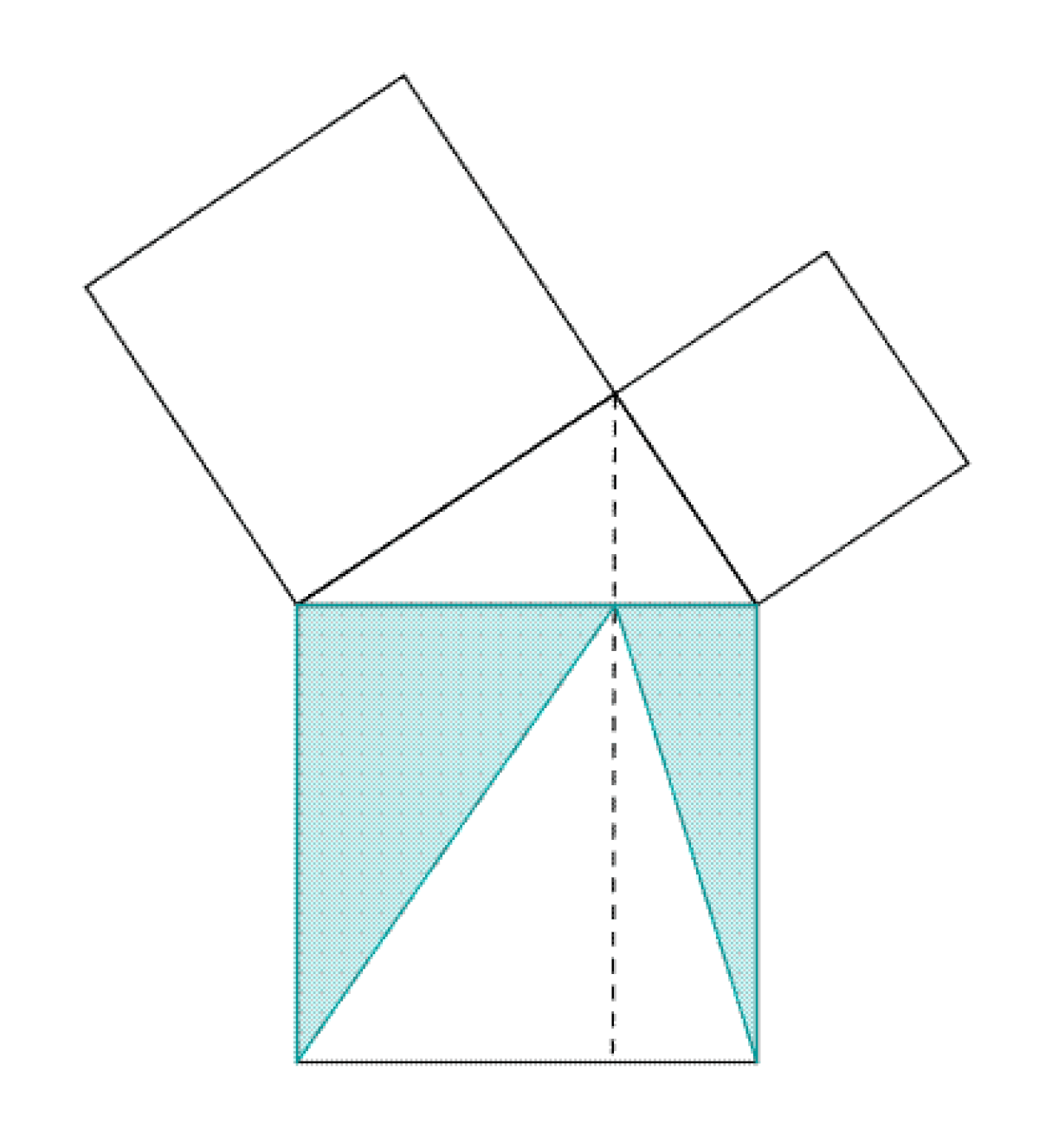
La figure du paragraphe illustre le mécanisme d'une preuve classique dans la démonstration d'un théorème, celui de Pythagore. Les triangles AEC et IBC sont semblables car le deuxième est la rotation d'un quart de tour du premier. Un triangle est donc une figure rigide qui possède une aire invariante par rotation.

Nombre et géométrie

Pour Euclide, le nombre est rationnel et répond à toutes les bonnes propriétés nécessaires. Dans son axiomatique, la question ne se pose pas. La connaissance actuelle des nombres montre que, s'il est possible de construire une géométrie sur les rationnels, le résultat n'est néanmoins pas celui espéré. Le corps de nombre n'est alors pas complet. La figure associée au paragraphe illustre alors l'anomalie, la rotation d'un quart de tour du segment orienté de la diagonale n'est plus un segment. En effet, le point A' n'existe pas. Ce segment possède une longueur de √2.

Une autre configuration, cette fois moins exotique, peut aussi se produire. En l'absence de précision, le corps de nombre peut être celui des complexes. Là encore, la géométrie est différente. Cette situation, compatible avec les axiomes d'Euclide, est bien connue à l'époque de la rédaction de l'article de Hilbert.

Rien, dans les axiomes ne garantit la présence d'un corps réel. En fait, la seule indication sur le corps de nombres sous-jacent est le troisième postulat, qui indique l'existence d'un cercle de rayon la longueur d'un segment.

Unicité de la géométrie

Une idée fréquente pendant plus des deux millénaires qui ont suivi l'édition des Éléments d'Euclide est le fait qu'il n'existe que deux uniques géométries, celle du plan euclidien, et celle de l'espace euclidien.

Elle se traduit par le statut donné au cinquième postulat, dit de la parallèle. Tel que formulé par Proclos, celui-ci stipule que « dans un plan, par un point distinct d'une droite d, il n'existe qu'une unique droite parallèle à d.» Si, comme on l'a cru jusqu'au début du XIX^e siècle l'unicité de la géométrie euclidienne est vraie, alors le cinquième postulat ne serait qu'un théorème, encore à l'état de conjecture. Il ne manquerait que le talent d'un mathématicien pour la démontrer, mais la proposition serait vraie et son statut de postulat ne serait que provisoire.

Il existe une infinité de droites qui, comme d1, d2 et d3, passent par le point M et sont parallèles à la droite D. Exemple de géométrie hyperbolique ne respectant pas le 5^e postulat d'Euclide.

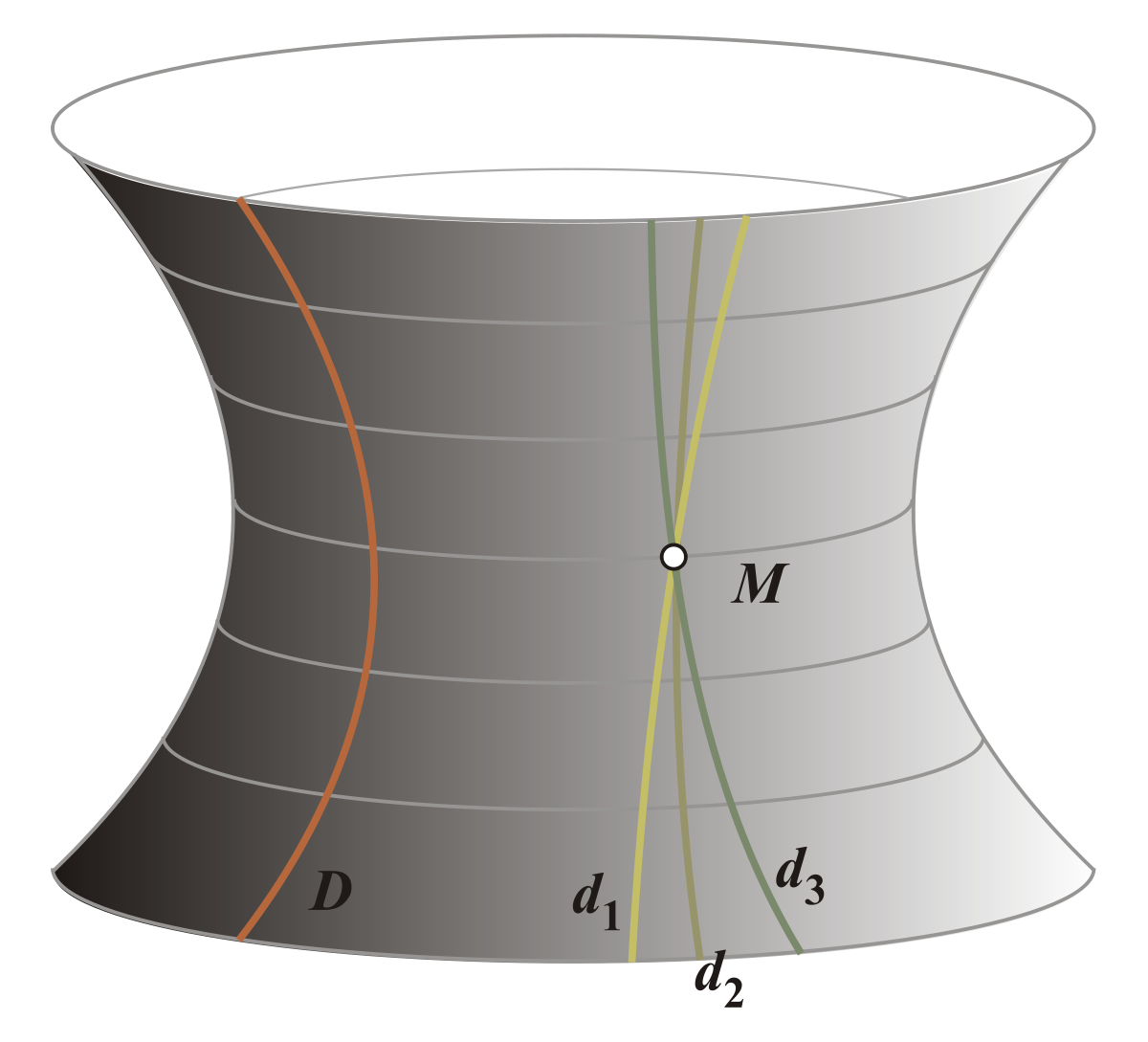
Mais lorsque Hilbert axiomatise la géométrie euclidienne, on sait déjà qu'il y a des géométries qui ne respectent pas le 5^e postulat. Dans son programme d'Erlangen, Felix Klein ordonne les différentes géométries : les espaces de Nikolaï Lobatchevski et Bernhard Riemann ne vérifient pas le 5^e postulat.

D'autres cas sont connus : Klein a construit un espace, celui de la figure qui respecte le cinquième postulat, mais qui n'est pas orientable. Dire qu'un espace est « orientable » signifie que la droite et la gauche existent. Dans un espace euclidien, une main droite et une main gauche ne sont jamais superposables, il est impossible de les faire coïncider sans utiliser une symétrie, c’est-à-dire une transformation équivalente à celle d'un miroir. La figure du paragraphe montre que cet état de fait n'est pas vrai dans toutes les géométries. Ainsi, la règle de la figure, jaune sous le plan et rouge au dessus, par un mouvement continu devient rouge sous le plan et jaune au dessus. Ce qui est impossible dans un plan euclidien.