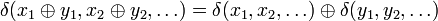Automate cellulaire - Définition

Classes remarquables d'automates cellulaires

Comme expliqué plus haut, les règles locales d'automates cellulaires sont trop nombreuses pour une étude exhaustive et la prédiction du comportement en fonction de la règle local est un problème très difficile en général. C'est pourquoi l'étude des automates cellulaires s'est souvent restreinte à des familles particulières, soit parce qu'elles se prêtent plus facilement à l'analyse, soit parce qu'elles correspondent à une propriété intéressante.

Automates réversibles

Un automate cellulaire A est réversible s'il existe un automate cellulaire B tel que les deux fonctions globales d'évolution F_A et F_B sont inverses l'une de l'autre : est la fonction identité. Intuitivement, B "remonte le temps" de l'évolution de A et, inversement, A "remonte le temps" de l'évolution de B. Par le théorème de Hedlund, on peut caractériser les automates cellulaires réversibles comme ceux dont la fonction globale est bijective.

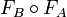
Cette classe a été très étudiée, notamment car elle fournit un modèle qui se rapproche du monde physique réel, supposé réversible à l'échelle microscopique (voir à ce sujet l'article sur la réversibilité et l'irréversibilité en thermodynamique). T. Toffoli et N. Margolus sont parmi les premiers à s'être intéressé spécifiquement aux automates cellulaires réversibles. L'intérêt réside aussi dans la recherche de systèmes de calcul réversibles supposés consommer moins d'énergie d'après le principe de Landauer. Il est aujourd'hui établi que certains automates cellulaires réversibles sont (travaux de Kenichi Morita).

Reconnaissance

Il est algorithmiquement impossible de distinguer les automates cellulaires réversibles de ceux qui ne le sont pas lorsque la dimension est supérieure à 2. En revanche, en dimension 1, il existe un algorithme très efficace.

Une autre façon de présenter cette différence entre la dimension 1 et les dimensions supérieures est la suivante : la taille du voisinage de l'inverse d'un automate A ne peut pas être borné récursivement en fonction de la taille du voisinage de A lorsque la dimension est 2 ou plus, alors qu'elle est bornée polynomialement en dimension 1 (un résultat récent montre même que la borne est linéaire).

Exemples

Technique du "second ordre" appliquée à l'automate cellulaire élémentaire 54 (le temps progresse de bas en haut).

Il est facile de construire des automates cellulaires réversibles. Pour cela, plusieurs formes de constructions existent.

1. la technique dite "du second ordre" : elle consiste à mélanger par une opération de OU exclusif bit à bit les informations du nouvel état d'une cellule avec son état passé. A priori, un automate cellulaire calcule la génération t + 1 en fonction de la génération t uniquement : la technique du second ordre paraît donc être une entorse au modèle. On peut contourner ce problème en fusionnant deux générations en une seule grâce à l'utilisation de plus d'états.
2. la technique des permutations par blocs alternées : elle a été proposée dans une version simple par Norman Margolus. Elle consiste à découper le réseau de cellules en blocs de cellules, à appliquer une permutation des états des cellules dans chaque bloc indépendamment, puis à décaler ce partitionnement et à appliquer une nouvelle permutation.
3. la technique du partitionnement : elle a été proposée par K. Morita et M. Harao. Elle consiste à appliquer une transformation purement locale sur chaque cellule, puis, en utilisant un partitionnement de l'ensemble d'états, à envoyer à chaque cellule voisine une certaine composante de cet état. Avec cette construction, on a la garantie que l'automate cellulaire est réversible si la transformation locale appliquée est elle même réversible.

Automates linéaires

Les automates cellulaires sont en général des systèmes dynamiques non-linéaires, ce qui rend leur étude par des outils classiques difficile. Mais cette vérité générale n'empêche pas certains automates cellulaires de posséder une forme plus ou moins stricte de linéarité.

Définition

Quelques étapes d'évolution sur une configuration périodique d'un automate cellulaire additif à 5 états, en dimension 2, et avec tous les a_i égaux à 1.

Formellement, un automate d'alphabet Q est dit linéaire si l'on peut munir Q d'une loi de groupe telle que :

Dans ce cas, si l'on étend à une opération agissant cellule à cellule sur l'espace des configurations, la fonction globale F_δ associée à l'automate est bien une fonction linéaire.

La linéarité facilite considérablement l'étude de la dynamique des automates. Ainsi, il suffit de connaître la dynamique d'un automate linéaire sur une "base" de l'espace de ses configurations pour en déduire par linéarité son comportement sur tout l'espace. On peut choisir pour une telle base l'ensemble (fini) des configurations partout égales à e (neutre de ) sauf éventuellement en la cellule centrale.

Automates additifs

L'une des familles les plus étudiées d'automates linéaires est celle des automates dits additifs, introduite par O. Martin, A. Odlyzko et S. Wolfram dans. Ces automates sont définis de la façon suivante :

• ,
• où les coefficients a_i sont fixés et caractérisent l'automate.

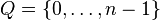
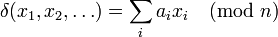
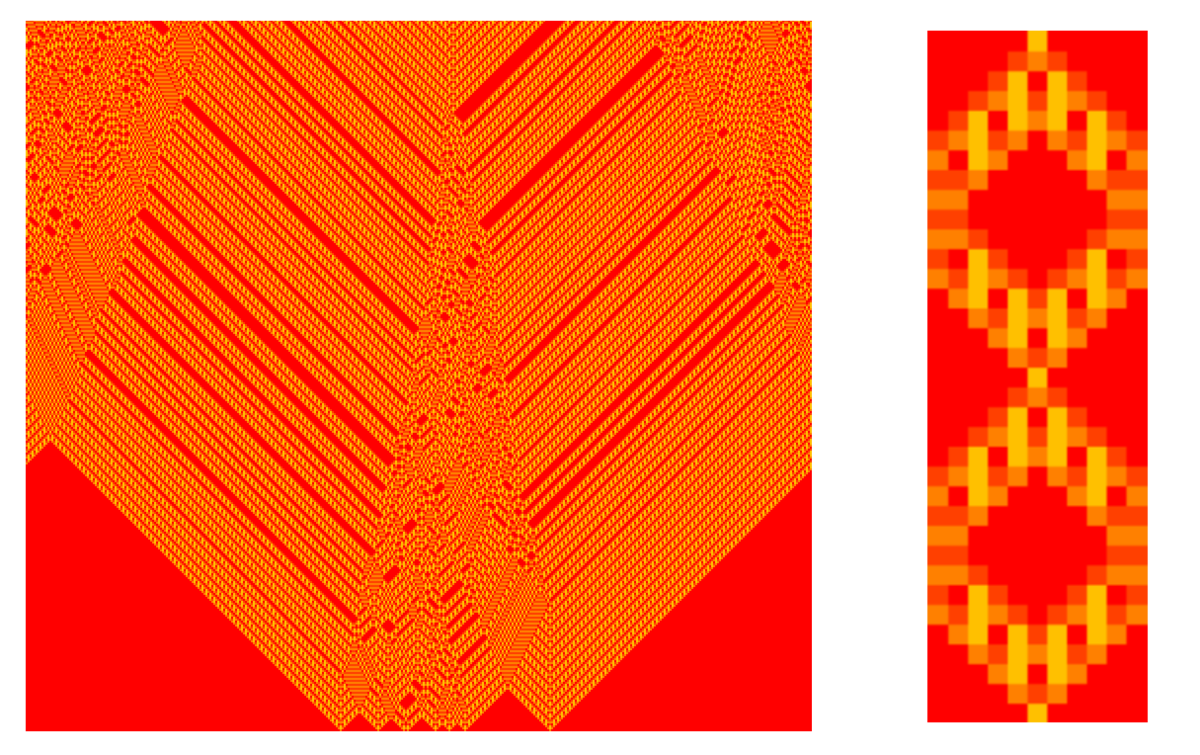
L'exemple typique est celui où tous les coefficients a_i sont égaux à 1 : la règle locale consiste alors à faire la somme modulo n de toutes les cellules du voisinage. Ainsi, en dimension 1, l' 90 est additif : sa fonction de transition consiste à faire la somme modulo 2 des états de la cellule et de ses deux voisines. Il suffit de connaître le comportement de cet automate sur la configuration c₀ partout égale à 0 sauf au centre où elle vaut 1 pour en déduire son comportement général par le principe de superposition :

L'automate élémentaire 102 est également additif. Son action sur la configuration c₀ produit un triangle de Pascal modulo 2 (qui donne aussi une approximation du triangle de Sierpinski). Ainsi, partant de c₀, la cellule z après t étapes se trouve dans l'état :

• 0 si z > 0 ou z < − t,
• dans les autres cas.

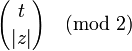
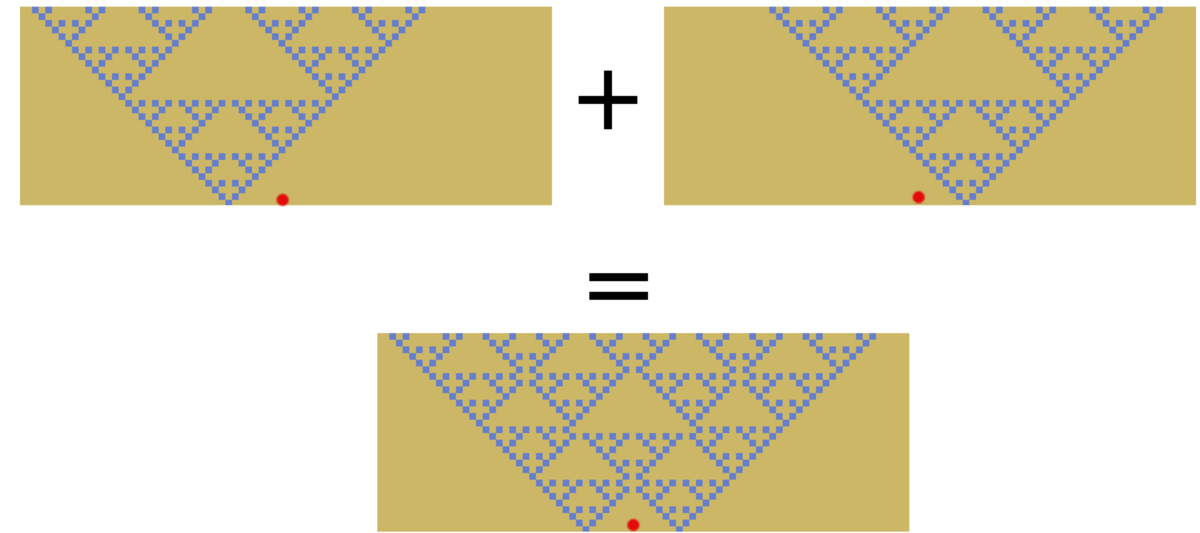
Par superposition, on en déduit une expression directe de l'état de la cellule centrale après t étape partant d'une configuration quelconque c :

• .

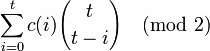
Automates totalistiques

Dans un automate cellulaire totalistique, l'état ultérieur d'une cellule ne dépend que de la somme des états de ses voisines ; c'est le cas du jeu de la vie où une cellule vivante le reste si deux ou trois de ses voisines sont vivantes, et une cellule morte naît si trois de ses voisines sont vivantes. Un automate totalistique ne prend donc pas en compte la position des voisines d'une cellule par rapport à celle-ci.

Automates sommatifs (totalistiques) tridimensionnels définis sur le voisinage rhomboédrique

Si un automate cellulaire n'est pas totalistique, en plus de leur état propre, la position des voisines d'une cellule influe sur son état ultérieur. Par exemple, pour un automate cellulaire à une dimension, on peut faire une différence entre la cellule voisine de gauche et la voisine de droite.

Automates conservatifs