Auguste De Morgan - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Enfance - Mathématique - Éducation universitaire - La loi de dualité - Budget de paradoxes

Introduction

Auguste De Morgan

Naissance	27 juin 1806 Madurai (Raj britannique maintenant Inde)
Décès	18 mars 1871 (à 64 ans) Londres (Angleterre)
Domicile	Angleterre Inde
Nationalité	Britannique
Champs	Mathématiques Logique
Institution	University College de Londres<
Diplômé	Trinity College (Cambridge) Université de Cambridge
Célèbre pour	Lois de De Morgan Algèbre universelle
Il est le père de William Frend De Morgan
modifier

Auguste De Morgan (27 juin 1806 à Madurai (Tamil Nadu) - 18 mars 1871) est un mathématicien et logicien britannique, né en Inde. Il est le fondateur avec Boole de la logique moderne ; il a notamment formulé les lois de De Morgan.

Enfance

Né d'un père colonel dans l'armée au service de la compagnie des Indes orientales, sa mère était une descendante de James Dodson, qui établit une table d'anti-logarithmes, c’est-à-dire les nombres correspondants pour extraire les logarithmes. À cause des révoltes, le colonel envoya sa famille en Angleterre quand Auguste avait sept mois. Dès lors il se considéra comme un Britannique au sens le plus large.

De Morgan perd son père l'année de ses dix ans. Avec sa mère qui voulait faire de son fils un religieux, ils habiteront dans diverses villes dans le sud-ouest de l'Angleterre ce qui lui fit changer souvent d'école. Ses talents mathématiques ont été découverts lorsqu'il avait quatorze ans. Un ami de la famille le trouva faisant un diagramme élaboré d'Euclide avec une règle et des compas et lui expliqua sa logique.

Auguste De Morgan avait un problème à un œil ce qui lui rendait plus difficile la pratique du sport et le rendait sujet à des moqueries. Il prétendait qu'il percevait néanmoins la distance et la solidité.

Mathématique

Auguste fut un écrivain brillant et plaisant, y compris dans sa correspondance, notamment avec William Hamilton.

Il n'aimait pas la campagne et tandis que sa famille profitait du bord de la mer, les hommes de science avaient du bon temps dans des clubs et lui restait dans des librairies poussiéreuses de la métropole. Il ne vota jamais à une élection ni ne visita les monuments.

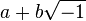
La meilleure présentation de sa conception de l'algèbre est dans trigonométrie et algèbre double publiée en 1849. L'étape suivante aurait du être l'algèbre 'triple' et si $a+b\sqrt{-1}$ représente vraiment une ligne dans un plan donné il devrait être possible de trouver un troisième terme qui ajouté aux précédent représenterait une ligne dans l'espace. Argand et quelque autres devinèrent que c'était $a + b\sqrt{-1} + c\sqrt{-1}\,^{\sqrt{-1}}$ bien que cela contredit la vérité établie par Euler que $\sqrt{-1}\,^{\sqrt{-1}}=e^{-\frac{1}{2} \pi}$ . De Morgan et bien d'autres travaillèrent dur au problème mais rien n'en sortit jusqu’à ce que le problème soit pris par Hamilton. Nous voyons maintenant la raison clairement: le symbole de la double algèbre dénote non une longueur et une direction mais un multiple et un angle. Dans celui-ci les angles sont confinés à un plan; donc l'étape suivante devrait être une algèbre quadruple quand l'axe du plan devient variable. Et cela donne la réponse à la première question; l'algèbre double n'est rien que de la trigonométrie analytique de plan, et c'est pourquoi il a été trouvé d'être l'analyse naturelle pour des courants alternés. Mais De Morgan n'alla jamais aussi loin.

Quand l'étude des mathématiques fut réactivée à l'université de Cambridge ce fut aussi le cas de la logique. La dynamique venait de Whewell. Dans logique formelle d'Auguste est intéressant sur le développement du syllogisme. Les aristotéliciens disent qu'à partir de deux propositions particulières comme quelques M sont des A et quelques M sont des B rien n'est obtenu de nécessaire dans la relation des A et B. Mais s'ils vont plus loin et disent que toute relation à propos des A et des B doivent suivre par nécessité le terme mitoyen doit être pris universellement dans l'une des prémisses. De Morgan signala qu'à partir de la plupart des M sont des A et la plupart des M sont des B on déduit que quelques A sont des B et il formula le syllogisme numérique qui met ce principe dans une forme quantitative précise. Suppose que le nombre de M est $m$ , des M qui sont des A est $a$ , et des M qui sont des B est $b$ ; alors il y a au moins $(a + b - m)$ A qui sont des B. Par exemple avec 1000 personnes sur un bateau dont 500 sont dans le salon et 700 meurent il est obligatoire qu'au moins 700+500-1000, donc 200 de ceux dans le salon furent des victimes.

Ici alors De Morgan fit une avance en introduisant la quantification des termes. À ce moment Hamilton enseignait à Édimbourg une doctrine de la quantification du prédicat et une correspondance se fit. Cependant De Morgan se rendit rapidement compte que la quantification d'Hamilton était d'une autre nature; qu'il voulait dire par exemple, en substituant les deux formes tout A est tout B et tout A est une partie de B pour la forme aristotélicienne Tout A est B. Les philosophes ont généralement une grande part d'intolérance pensant qu'ils ont la totalité de la vérité. Hamilton pensa qu'il avait placé la clé de voûte dans la construction aristotélicienne bien qu'il aurait été étrange qu'elle exista pendant deux millénaires sans ce facteur essentiel. Comme conséquence il n'avait aucune place pour les innovations de De Morgan qu'il accusa d'être un plagiaire et la dispute continua entre eux pendant des années.