Arithmétique modulaire - Définition

Introduction

Couverture de l’édition originale des Recherches arithmétiques de Gauss, livre fondateur de l’arithmétique modulaire.

En mathématiques et plus précisément en théorie algébrique des nombres, l’arithmétique modulaire est un ensemble de méthodes permettant la résolution de problèmes sur les nombres entiers. Ces méthodes dérivent de l’étude du reste obtenu par une division euclidienne.

L'idée de base de l'arithmétique modulaire est de travailler non sur les nombres eux-mêmes, mais sur les restes de leur division par quelque chose. Quand on fait par exemple une preuve par neuf à l'école primaire, on effectue un peu d'arithmétique modulaire sans le savoir : le diviseur est alors la valeur 9.

Si ses origines remontent à l’Antiquité, les historiens associent généralement sa naissance à l’année 1801, date de la publication du livre Disquisitiones arithmeticae de Carl Friedrich Gauss . Sa nouvelle approche permet d’élucider de célèbres conjectures et simplifie les démonstrations d’importants résultats par une plus grande abstraction. Si le domaine naturel de ces méthodes est la théorie des nombres, les conséquences des idées de Gauss se retrouvent dans d’autres champs des mathématiques, comme l’algèbre ou la géométrie.

Le XX^e siècle modifie le statut de l’arithmétique modulaire. D’une part, d’autres méthodes sont nécessaires pour progresser en théorie des nombres. D’autre part, le développement de nombreuses applications industrielles impose la mise au point d’algorithmes issus des techniques modulaires. Ils résolvent essentiellement des questions soulevées par la théorie de l’information, une branche maintenant surtout considérée comme des mathématiques appliquées.

L’article congruence sur les entiers propose une introduction plus mathématique, anneau Z/nZ traite le même sujet de manière moins didactique et plus exhaustive.

Usages

En mathématiques pures, ce terme est très peu utilisé. Le vocable proche le plus fréquent est théorie algébrique des nombres, qui désigne un domaine plus large, contenant par exemple les notions d'entiers algébriques et de théorie de Galois.

En mathématiques appliquées, cette expression est d'un usage fréquent pour décrire les bases mathématiques de différents domaines de la théorie de l'information : cryptologie, théorie des codes et informatique. De nombreux outils et algorithmes entrent dans ce champ d'étude. On y trouve les tests de primalités, la décomposition en produit de facteurs premiers, l'utilisation des caractères d'un groupe par exemple pour la transformée de Fourier discrète ou encore l'étude d'autres quotients que ceux des entiers, comme celui des polynômes.

Selon les différents auteurs et le domaine d'application, ces extensions sont considérées, soit comme une partie intégrante de l'arithmétique modulaire, soit comme des applications, voire ne sont pas citées du tout. Sous sa forme simple, elle prend parfois le nom d'arithmétique de l'horloge. Le terme de système modulaire est utilisé pour désigner une arithmétique modulaire sur d'autres ensembles que les entiers.

Outils de l'arithmétique modulaire

Congruence et les entiers

L'exemple historique de l'« arithmétique modulaire » repose sur les nombres entiers. Un entier n étant fixé, le calcul modulo n consiste à identifier tous les entiers à leur reste dans la division euclidienne par n ; ceci peut être illustré par l'exemple de l'« arithmétique de l'horloge », qui correspond à n=12 : la petite aiguille se trouve dans la même position à deux moments éloignés de douze heures, on identifie par exemple 13 h à 1 h. Pour obtenir un calcul sur un tel ensemble, on vérifie que l'addition et la multiplication sont compatibles avec les identifications. Cette formalisation est l'œuvre de Legendre, qui donne le nom de résidu aux différents éléments.

L'apport de Gauss consiste à analyser la structure de cet ensemble, maintenant qualifié du nom d'anneau de congruences et noté Z/nZ. Elle se divise en premier lieu en l'étude de l'addition, qui définit un groupe cyclique de générateur 1 ; puis de la multiplication, qui dépend des propriétés du modulo. Si celui-ci est premier, on obtient un corps. Cette approche simplifie les démonstrations arithmétiques. Les deux exemples historiques du livre Disquisitiones arithmeticae sont le théorème de Wilson et le petit théorème de Fermat.

Le calcul modulaire, dans le cas où le modulo n'est pas premier, est plus complexe. Le théorème des restes chinois permet d'élucider la structure. L'anneau n'est pas intègre, il existe des diviseurs de zéro, ce sont des nombres qui, multipliés par un certain autre nombre non nul, donnent zéro. Le nombre d'éléments inversibles est donné par la fonction indicatrice d'Euler. Elle permet, par exemple, de généraliser le petit théorème de Fermat.

Résidu et polynôme

Figure à la règle et au compas: l'heptadécagone, un polygone régulier de 17 côtés, mis en évidence avec les techniques de l'arithmétique modulaire.

Gauss remarque que l'ensemble des polynômes à coefficients rationnels peut se voir appliquer la logique du calcul modulaire, puisqu'il dispose d'une addition, d'une multiplication, et d'une division euclidienne. Les congruences sont les restes de la division euclidienne des polynômes par un polynôme donné.

Il applique cette approche au polynôme Xⁿ - 1 et trouve sa décomposition en produit de facteurs irréductibles, qui prennent le nom de polynôme cyclotomique. Gauss utilise ces résultats pour trouver une construction à la règle et au compas de l'heptadécagone, polygone régulier à 17 côtés.

Il hésite à considérer ces travaux comme de l'arithmétique ; il écrit : « La théorie de la division du cercle, ou des polygones réguliers, ..., n'appartient pas par elle même à l'Arithmétique, mais ses principes ne peuvent être puisés que dans l'Arithmétique transcendante ». Le terme d'arithmétique « transcendante » de Gauss est maintenant remplacé par celui d'arithmétique « modulaire ». La logique de cet argument est toujours d'actualité.

Entier algébrique

Le cas des polynômes à coefficients entiers diffère : la propriété de division ne fonctionne que pour des polynômes dont le plus grand coefficient est égal à plus ou moins un. Le cas des moduli du polynôme X² + 1 est envisagé : la structure modulaire obtenue est encore celle d'un anneau, s'identifiant à l'ensemble des nombres de la forme α + i.β où α et β sont des entiers et i désigne le nombre imaginaire, correspondant au monôme X. Cet ensemble est celui des entiers de Gauss.

Illustration de la division euclidienne pour les entiers de Gauss

Illustration de la démonstration du théorème des deux carrés par les entiers de Gauss

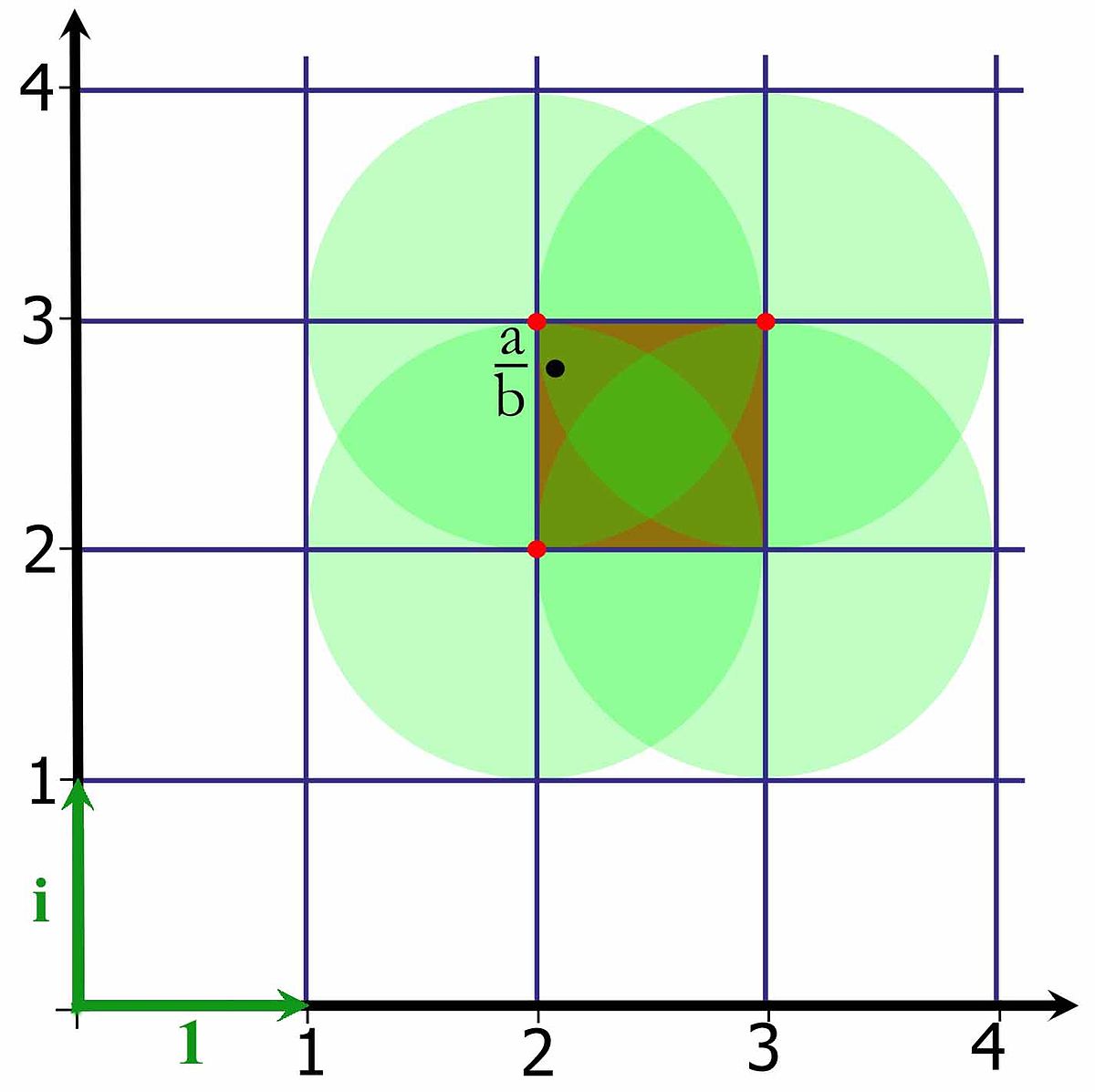
Il peut être muni d'une norme. À l'entier de Gauss a = α + i.β est associée la norme α² + β², qui provient du module des nombres complexes. Cette norme permet de définir une division euclidienne, comme l'illustre la figure de droite. Les entiers sont représentés par les intersections du quadrillage. La valeur a/b existe si b est différent de zéro, cependant cette valeur n'est pas nécessairement un entier de Gauss. Elle est représentée par le point noir de la figure. Dire qu'une division euclidienne existe, revient à dire qu'il existe un entier de Gauss à une norme strictement inférieure à un de ce point noir. L'illustration montre que, dans le cas présent, il existe au moins trois candidats. Dans le cas général, il en existe entre un et quatre et dans ce contexte seule l'existence compte.

Ce résultat de division euclidienne implique des propriétés sur cet anneau d'entiers : l'identité de Bézout, l'existence de nombres premiers de Gauss et un analogue du théorème fondamental de l'arithmétique. Ces nombres premiers permettent à Richard Dedekind de proposer une résolution simple du théorème des deux carrés. L'illustration géométrique est donnée sur la figure de gauche. Un nombre premier p s'exprime comme somme de deux carrés si le cercle de rayon la racine de p croise au moins un entier Gauss.

Ferdinand Eisenstein , qui rencontre Gauss en 1844, découvre un nouvel anneau d'entiers ; l'arithmétique sur cet anneau offre une démonstration rigoureuse du grand théorème de Fermat pour n égal à trois, justifiant, encore une fois, la nécessité théorique d'une telle généralisation de l'arithmétique modulaire.

Caractère de Dirichlet

Peter Dirichlet développe l'essentiel de la théorie dans le cadre de l'anneau Z/nZ.

Dirichlet s'intéresse aux nombres premiers de la forme n + λ.m où n et m sont deux entiers premiers entre eux et λ une variable qui décrit l'ensemble des entiers positifs. Il souhaite en effet démontrer qu'il existe une infinité de nombres premiers de cette nature.

L'arithmétique modulaire est un bon outil pour cette problématique, qui est équivalente à trouver le cardinal de l'ensemble des nombres premiers dans une classe de modulo.

Dirichlet considère le groupe des éléments inversibles modulo m, et étudie l'ensemble des fonctions du groupe dans les nombres complexes non nuls qui vérifient, si a et b sont deux résidus : f(a.b) = f(a).f(b). De telles fonctions sont appelées caractères de Dirichlet. Il en existe φ(n), le produit de deux caractères est encore un caractère, et leur table de multiplication est exactement la même que celle du groupe des unités étudié.

Les calculs sur ces fonctions sont formellement analogues à ceux réalisés précédemment par Joseph Fourier . Il faut néanmoins atteindre le XX^e siècle pour voir apparaître une théorie unifiant les deux approches. Elle prend le nom d'analyse harmonique.