Arithmétique modulaire - Définition

Développements théoriques

Il est fréquent que des concepts mathématiques, développés dans un contexte, soient réutilisés dans d'autres domaines. Ainsi la théorie des groupes s'applique à l'arithmétique et à la géométrie. Il en est de même pour les outils de l'arithmétique modulaire, dont les outils alimentent de vastes champs des mathématiques pures, comme l'algèbre générale ou la théorie de Galois. Ces théories ne sont néanmoins pas considérées comme des cas particuliers d'arithmétique modulaire car elles font aussi appel à de nombreux autres concepts.

Structure quotient

En langage moderne, l'arithmétique modulaire se formalise par la notion de quotient d'anneaux euclidiens. Le concept de relation d'équivalence permet de généraliser ce concept aux principales structures algébriques. Par exemple, le quotient d'un groupe par un sous-groupe normal est, à travers le théorème de Jordan-Hölder, un outil de base de la classification des groupes finis. Les groupes quotients sont aussi utilisés en topologie algébrique pour classifier les variétés. Dans la théorie des anneaux, la notion d'idéal joue un rôle analogue à celui de la notion de sous-groupe normal en théorie des groupes. Elle permet de construire des anneaux quotients dans un contexte plus général que celui de l'arithmétique modulaire. Le théorème des zéros de Hilbert, base du lien entre l'algèbre commutative et la géométrie algébrique, s'exprime en termes d'idéal.

Les termes de congruence et de modulo sont néanmoins réservés aux quotients sur un anneau euclidien.

Résidus de polynômes et théorie de Galois

Évariste Galois est le fondateur de la théorie portant maintenant son nom.

L'arithmétique modulaire s'applique à l'anneau des polynômes à coefficients dans un corps, car cette structure dispose d'une division. Elle est le point de départ de la théorie d'Évariste Galois et consiste en l'étude systématique des ensembles de congruence de polynômes modulo un polynôme irréductible, l'équivalent des nombres premiers. Ces ensembles sont maintenant appelés extensions algébriques.

Ces extensions permettent l'analyse de la résolubilité des équations algébriques, c'est-à-dire des équations s'écrivant sous forme polynomiale. Si le polynôme est irréductible, son ensemble de congruences est le plus petit corps contenant au moins une racine. Il est appelé corps de rupture. En réitérant ce processus, un corps contenant toutes les racines, le corps de décomposition, est construit. La logique modulaire du quotient fournit la structure algébrique adaptée à cette problématique.

La théorie de Galois fait appel à bien d'autres notions. L'étude de la résolubilité de l'équation est possible via l'étude du groupe des automorphismes du corps, appelé groupe de Galois, grâce à la correspondance de Galois entre sous-corps et sous-groupes. Au-delà de l'étude de la résolubilité des équations algébriques, la théorie de Galois est devenue un cadre naturel de résolution de nombreux problèmes en arithmétique, géométrie arithmétique ou géométrie algébrique, et permet surtout de formuler de nouveaux problèmes plus généraux dans ces divers domaines.

Si cette théorie utilise le concept de quotient d'un anneau euclidien, la variété d'outils spécifiques à ce domaine en fait un champ propre, bien distinct du sujet de cet article. L'un des fruits de cette théorie, les corps finis, encore appelés corps de Galois, fournissent un cadre naturel à de nombreuses applications en arithmétique modulaire.

Entier algébrique et théorie algébrique des nombres

Ernst Kummer démontre le dernier théorème de Fermat pour de nombreuses valeurs de n et fonde la théorie algébrique des nombres.

L'arithmétique modulaire offre un bon cadre conceptuel pour la résolution du grand théorème de Fermat. Cependant, si n est plus grand que dix, les anneaux d'entiers algébriques, construits selon la méthode de Gauss, présentent ce que Dirichlet appelle une obstruction. Il montre que le groupe des unités de cet anneau, c'est-à-dire des éléments ayant un inverse pour la multiplication, n'est plus un groupe cyclique ou abélien fini comme celui qu'étudiait Gauss. Il contient aussi des copies de l'anneau des entiers et est donc infini. Ce résultat prend le nom de théorème des unités de Dirichlet. L'obstruction provient de cette nouvelle configuration. Elle empêche l'application des techniques modulaires utilisées pour les entiers de Gauss car l'anneau associé n'est plus euclidien.

Ernst Kummer utilise un outil lié à la généralisation du quotient maintenant formalisé par les idéaux. Ils remplacent les nombres premiers absents. La théorie algébrique des nombres prend alors le relais, avec des techniques différentes. L'outil de base est un anneau dont les éléments sont appelés entiers algébriques et qui possède une structure dite d'anneau de Dedekind. Kummer parvient ainsi à démontrer le grand théorème pour certaines valeurs de n premier, c'est-à-dire pour les nombres premiers réguliers. Les seules valeurs inférieures à 100 non traitées sont 37, 59 et 67.

D'autres outils et objets d'étude apparaissent, comme l'anneau adélique, ceux de la théorie de Galois, les courbes elliptiques, les séries L de Dirichlet ou les formes modulaires. Certains proviennent de conséquences presque directes de l'arithmétique modulaire, comme les corps finis, utilisés de manière intensive au XX^e siècle. La théorie algébrique des nombres est largement plus vaste que le cadre de l'arithmétique modulaire, tout en reposant in fine sur des techniques parfois similaires.

Caractère de Dirichlet et théorie analytique des nombres

Représentation de la valeur absolue de la fonction zêta de Riemann.

Bernhard Riemann émet l'hypothèse de localisation des racines de la fonction ζ (zêta).

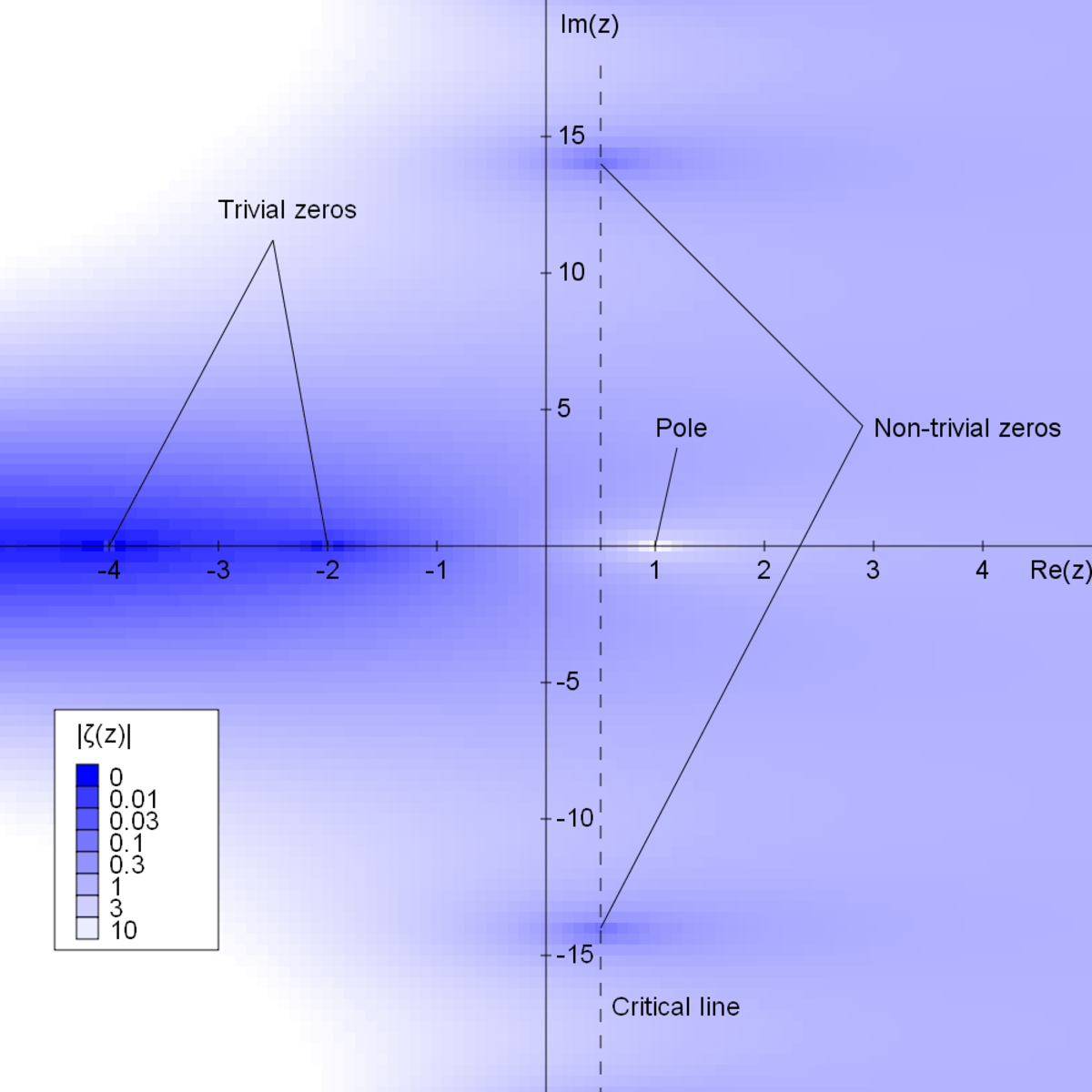
La découverte par Euler d'un produit infini, construit à l'aide de nombres premiers et égal au sixième du carré de la surface d'un cercle de rayon un, ouvre la voie à une approche différente pour la compréhension des nombres. Dirichlet l'utilise pour démontrer que chacun des moduli d'entiers du groupe des unités contient une infinité de nombres premiers. Ce résultat porte maintenant le nom de théorème de la progression arithmétique.

Pour mener à bien sa démonstration, Dirichlet développe un outil spécifique, les séries L de Dirichlet. L'une de ses séries correspond à une célèbre fonction qui prendra le nom de ζ (zêta) de Riemann. Sa plus grande difficulté consiste à prouver que ses fonctions n'ont pas de racine au point un. Pour y parvenir, il utilise l'analyse harmonique sur le groupe des unités d'une classe de modulo.

Néanmoins, une fois encore, l'arithmétique modulaire est insuffisante pour venir à bout du théorème. Dirichlet utilise de nombreuses techniques analytiques, comme les séries entières et l'analyse complexe. Le fruit de ces travaux donne naissance à une nouvelle branche des mathématiques : la théorie analytique des nombres. L'un des points cruciaux de cette théorie provient de l'unique article de Bernhard Riemann en théorie des nombres : Sur le nombre de nombres premiers inférieurs à une taille donnée. Il conjecture une localisation des racines de sa fonction ζ. La recherche de la position des racines, initiée par Dirichlet, devient une préoccupation centrale et reste l'une des conjectures pressenties comme les plus difficiles des mathématiques de notre époque.