Architecture Dataflow - Définition

Introduction

Un ordinateur dataflow (flot de données) décrit une architecture où les données sont des entités actives qui traversent le programme de manière asynchrone, contrairement à l'architecture classique von Neumann où elles attendent passivement en mémoire pendant que le programme est exécuté séquentiellement suivant le contenu du pointeur de programme (PC). On parle aussi d'ordinateur cadencé par les données.

Principe de fonctionnement

Dans une architecture flot de données, les programmes sont représentés sous forme de graphes : un nœud représente une opération à effectuer, tandis que les données circulent sur les arcs et forment les entrées aux nœuds. Les données sont transportées par des jetons (token). La règle de base, dite de déclenchement, instaure que lorsqu'un nœud voit toutes ses entrées satisfaites, il est activé et produit une valeur en sortie, et les jetons présents en entrées sont supprimés.

Ces architectures sont étroitement couplées aux langages de programmation fonctionnelle. Elles ne génèrent pas d'effet de bord, donc ne nécessite pas de mémoire partagée, ni de séquenceur ou pointeur de programme.

Elles sont aussi éminemment parallèles : l'unité responsable de l'exécution des instructions issue de la mémoire contenant le programme doit posséder un nombre relativement élevé de processeurs (16 et au dessus) afin de maximiser la puissance totale de l'ordinateur.

Plusieurs unités de calcul traitant des données différentes les classent dans la famille des ordinateurs MIMD (Multiple Instructions, Multiple Data).

Structure des graphes

Pour mieux comprendre comment les programmes flot de données peuvent être exécutés par un ordinateur, il est plus aisé de représenter les graphes sous la forme d'une collection de structures reliées entre elles par des pointeurs.

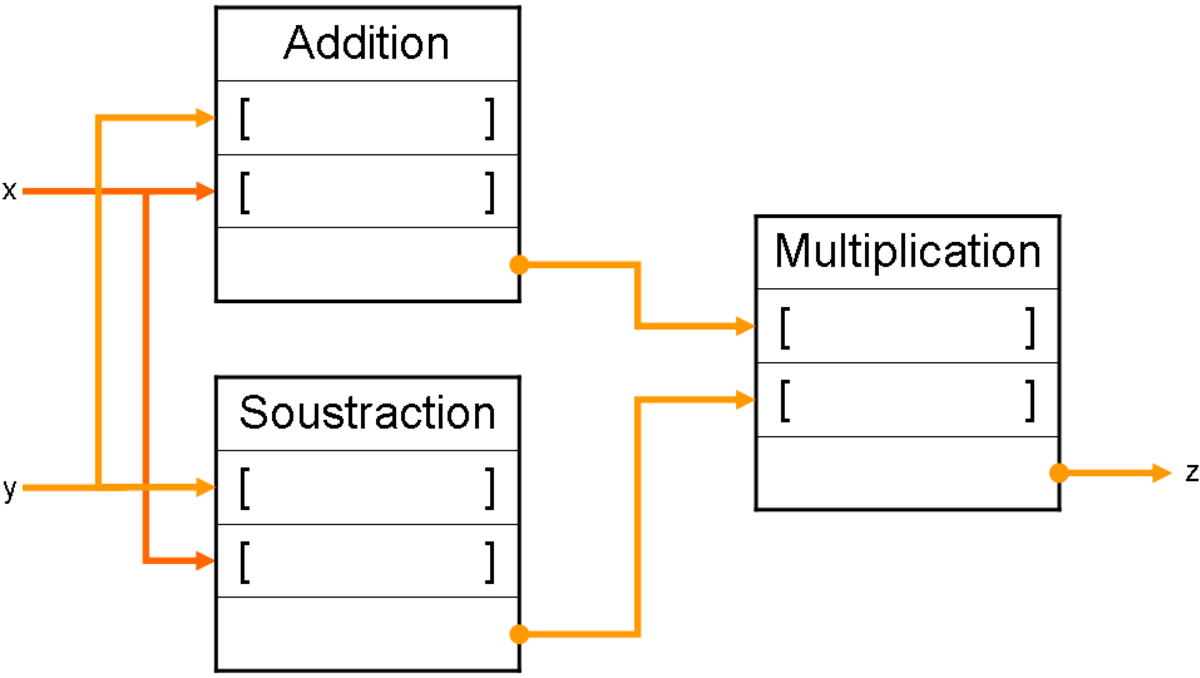
Le premier graphe z = (x + y) × (x - y) peut être représenté par cette structure :

Représentation structurelle de l'expression z = (x + y) × (x - y).

Chaque nœud est représenté par un bloc dont le premier élément est l'opération à effectuer, puis suivent les emplacements indiqués par de parenthèses « [ ] » qui sont destinés à contenir les paramètres de l'opération, ainsi que des emplacement contenant les adresses où sera placé le résultat. Certains emplacements peuvent éventuellement contenir des constantes.

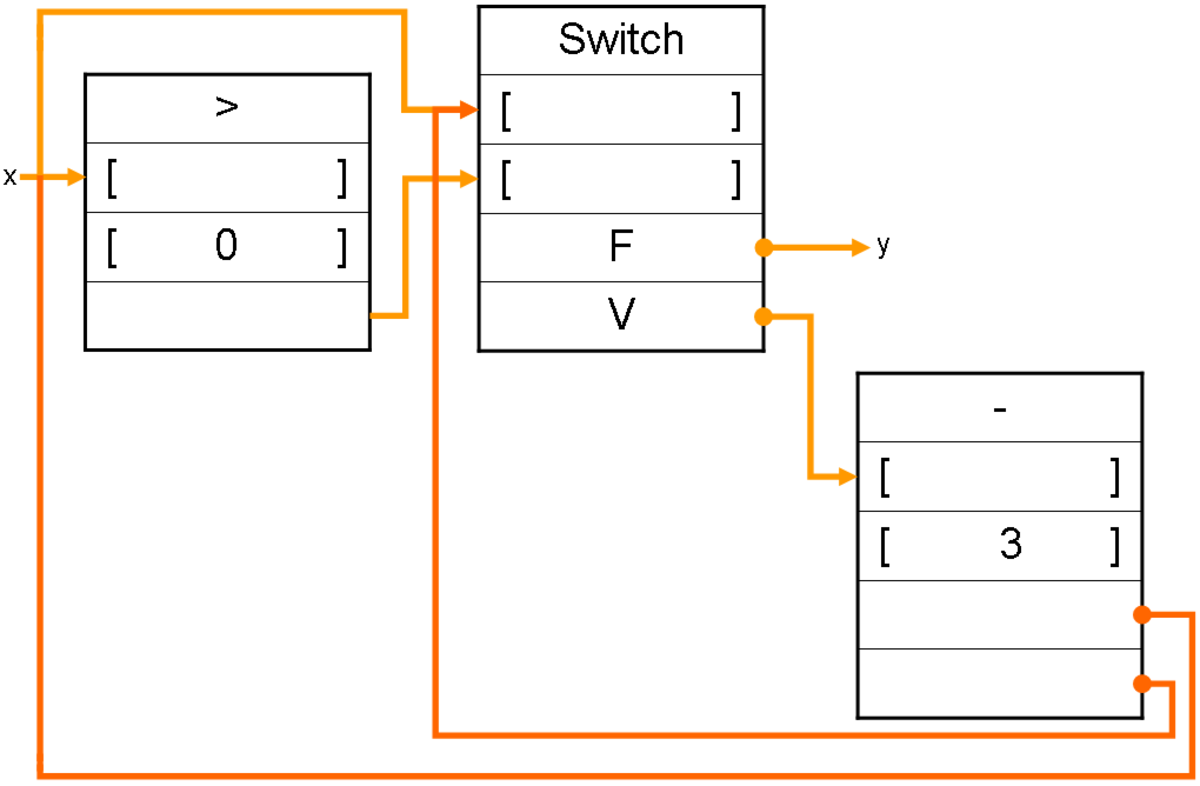
Les itérations ne posent pas de problème non plus, ci dessous la structure de la boucle WHILE précédemment évoquée :

Représentation structurelle d'une itération.

Les graphes comme langage

Un nœud computationnel peut être représenté comme le sommet d'un graphe. Les jetons circulent sur les arcs reliant les sommets.

Quand deux jetons contenant respectivement les valeurs 3 et 5 se présentent aux entrées du nœud, celui-ci exécute l'opération pour laquelle il est conçu (ici une addition), génère un jeton en sortie représentant la somme (3 + 5), 8, et supprime les jetons d'entrées :

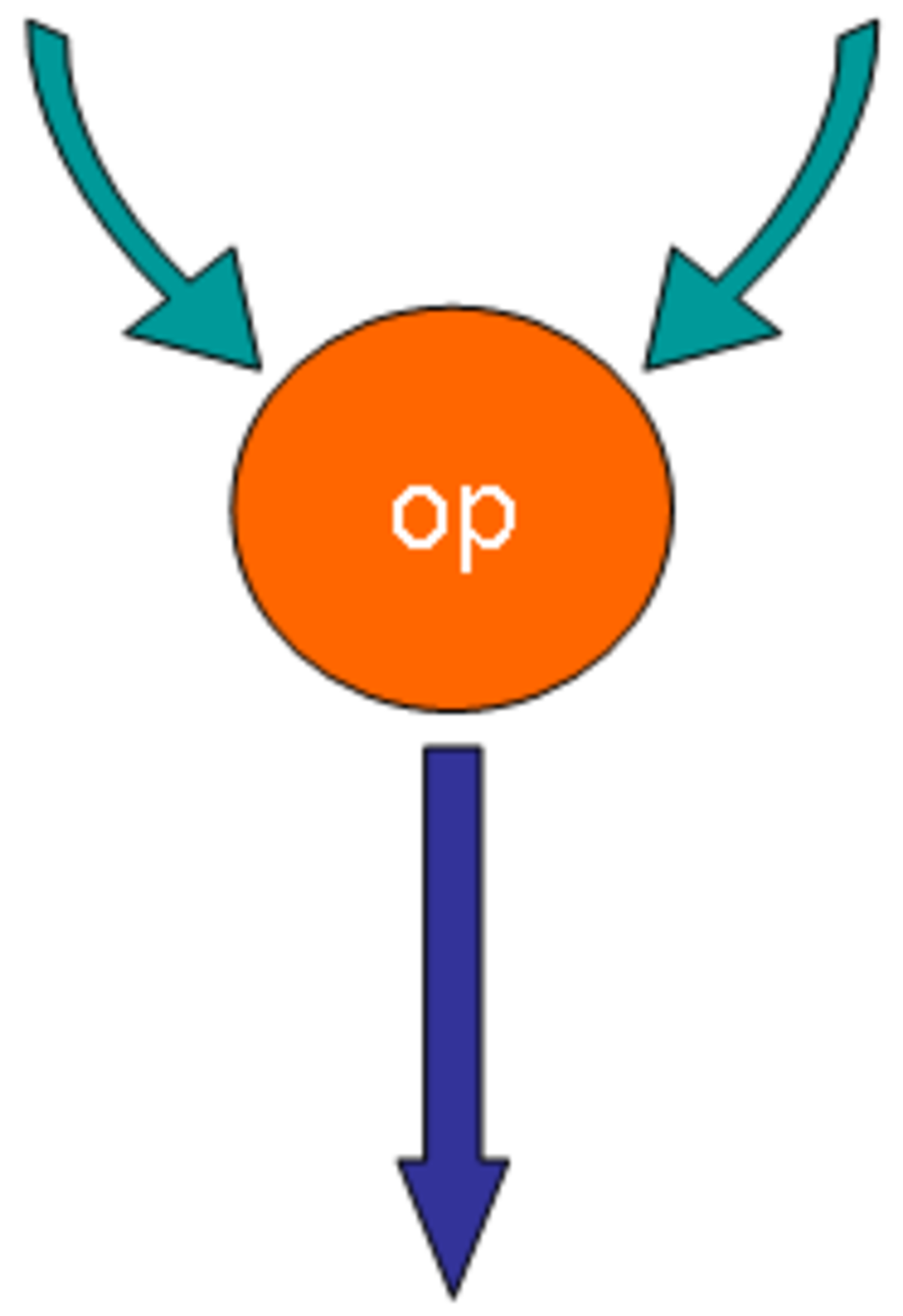
Un nœud de base d'une architecture dataflow.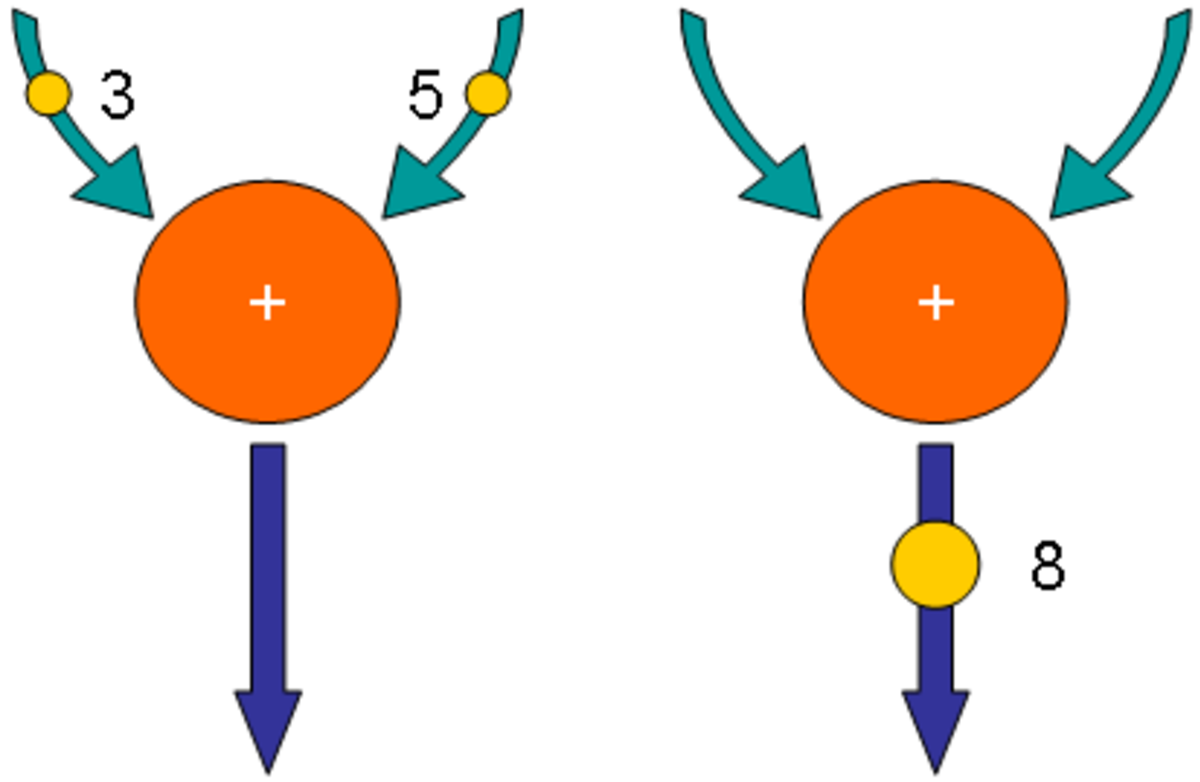

Activation d'un nœud. Notez la disparition des jetons d'entrées après la production d'une valeur en sortie.

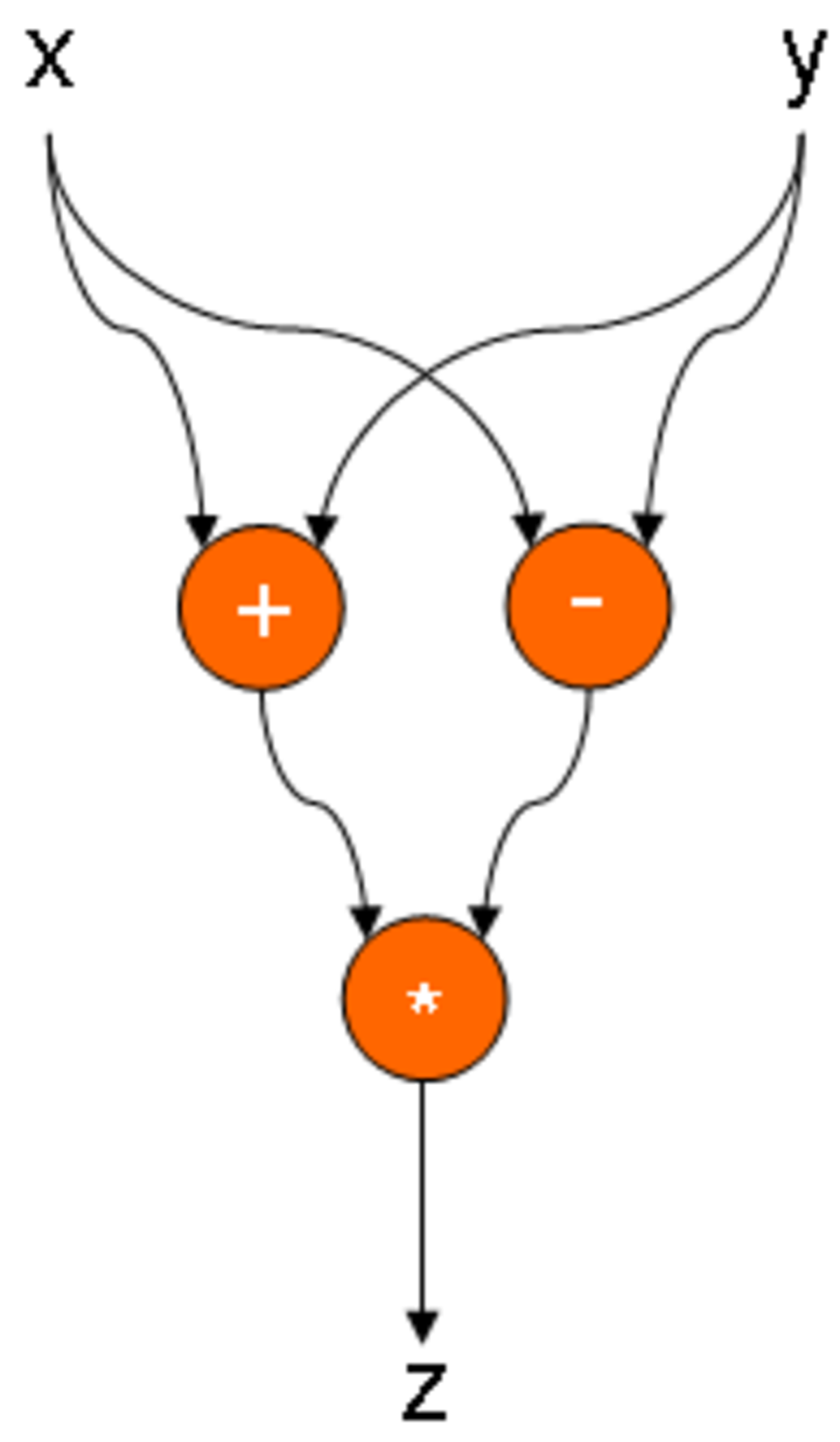
L'expression plus complexe z = (x + y) × (x - y) correspond au graphe ci dessous. On constate que le parallélisme est implicite : les deux nœuds + et - sont activables simultanément.

Le programme (graphe) correspondant à l'expression z = (x + y) * (x - y).

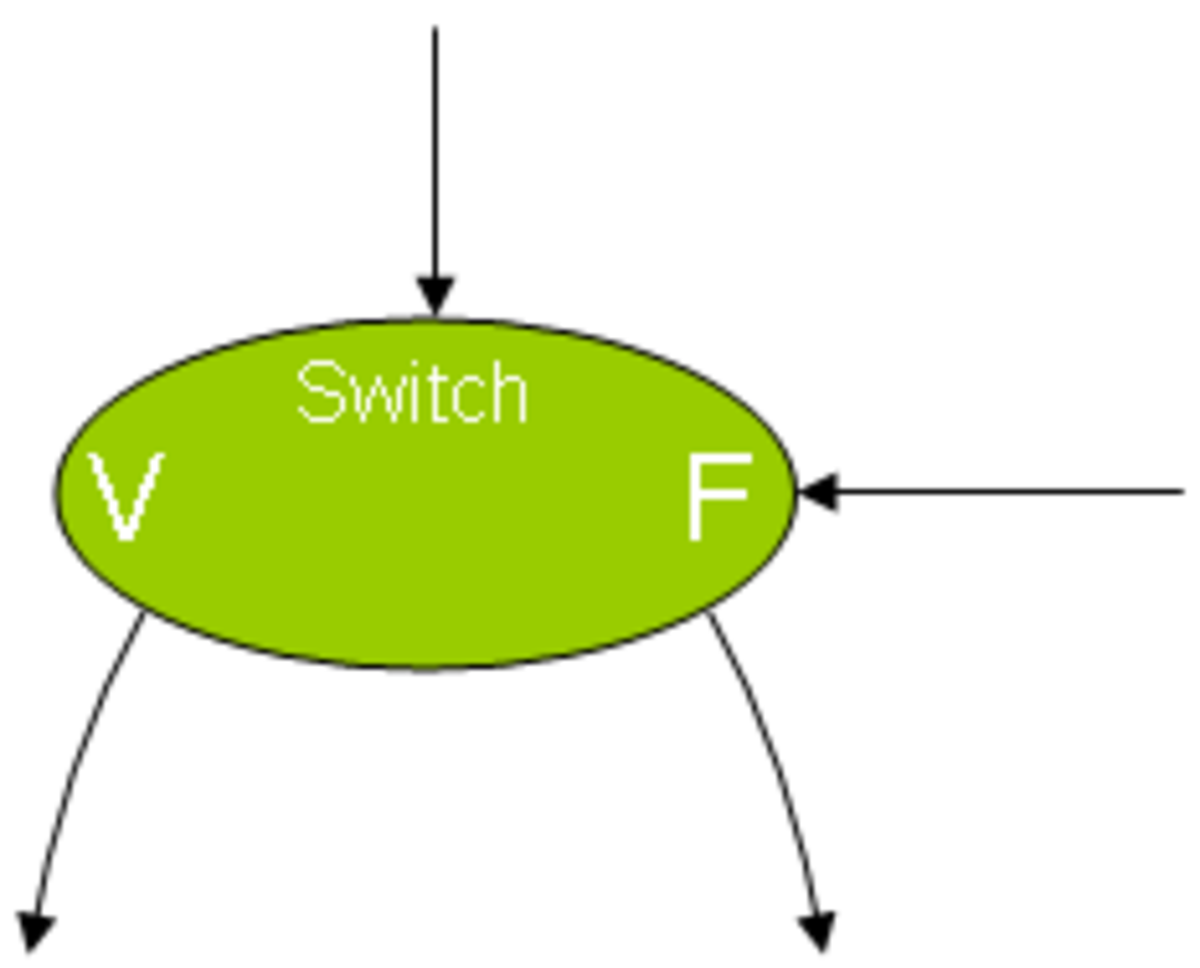
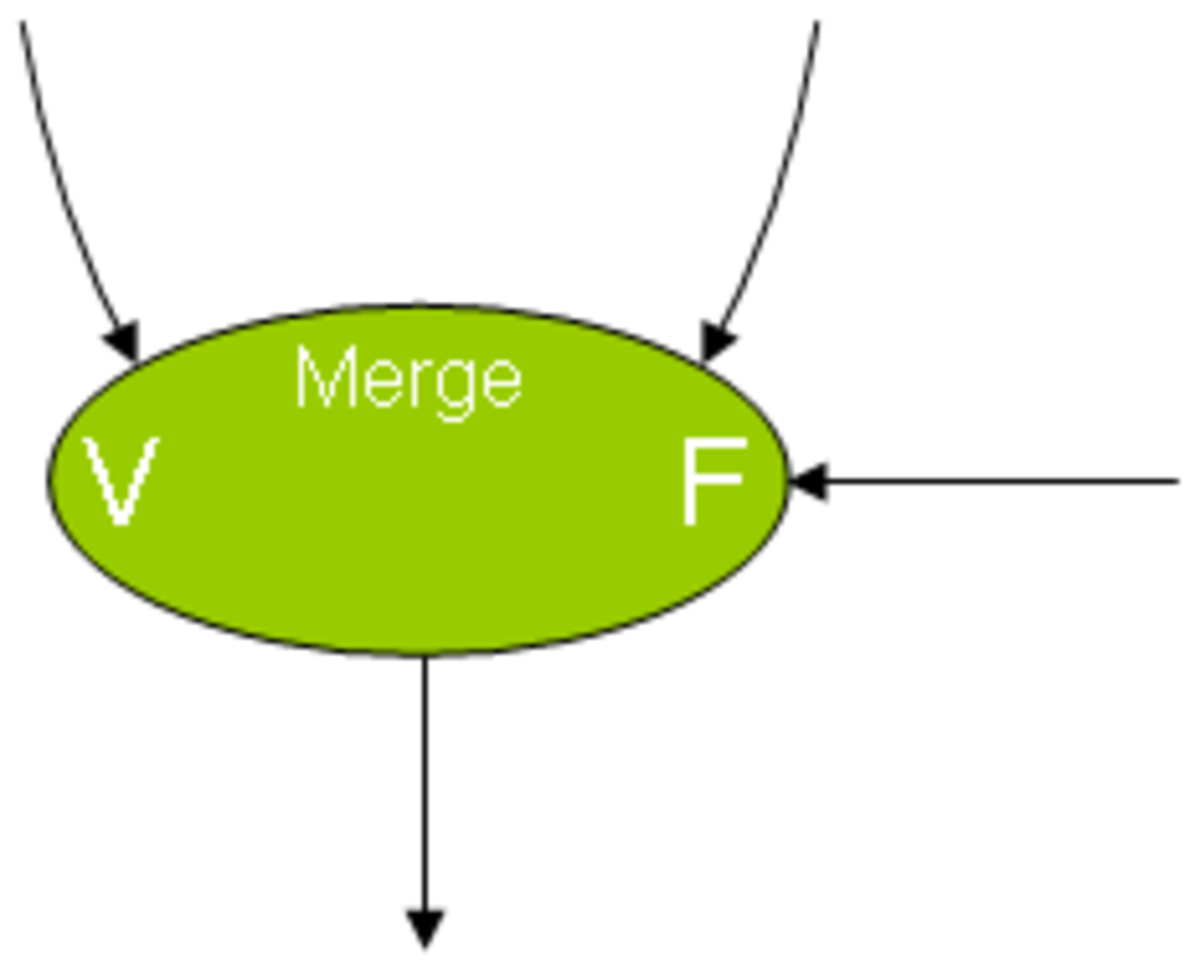
Grâce à deux types de nœuds appelés switch et merge, on peut coder la condition si. Le premier type possède deux entrées et deux sorties, tandis que le second possède trois entrées et une sortie. Le type switch répercutera son jeton d'entrée sur l'une ou l'autre de ses sorties suivant l'état de sa seconde entrée. Le type merge fera la sélection d'un de ses deux jetons d'entrée suivant la valeur d'un troisième. Schématiquement :

Un nœud de type switch. V et F tiennent lieu de Vrai et Faux.

Un nœud de type merge. V et F tiennent lieu de Vrai et Faux.

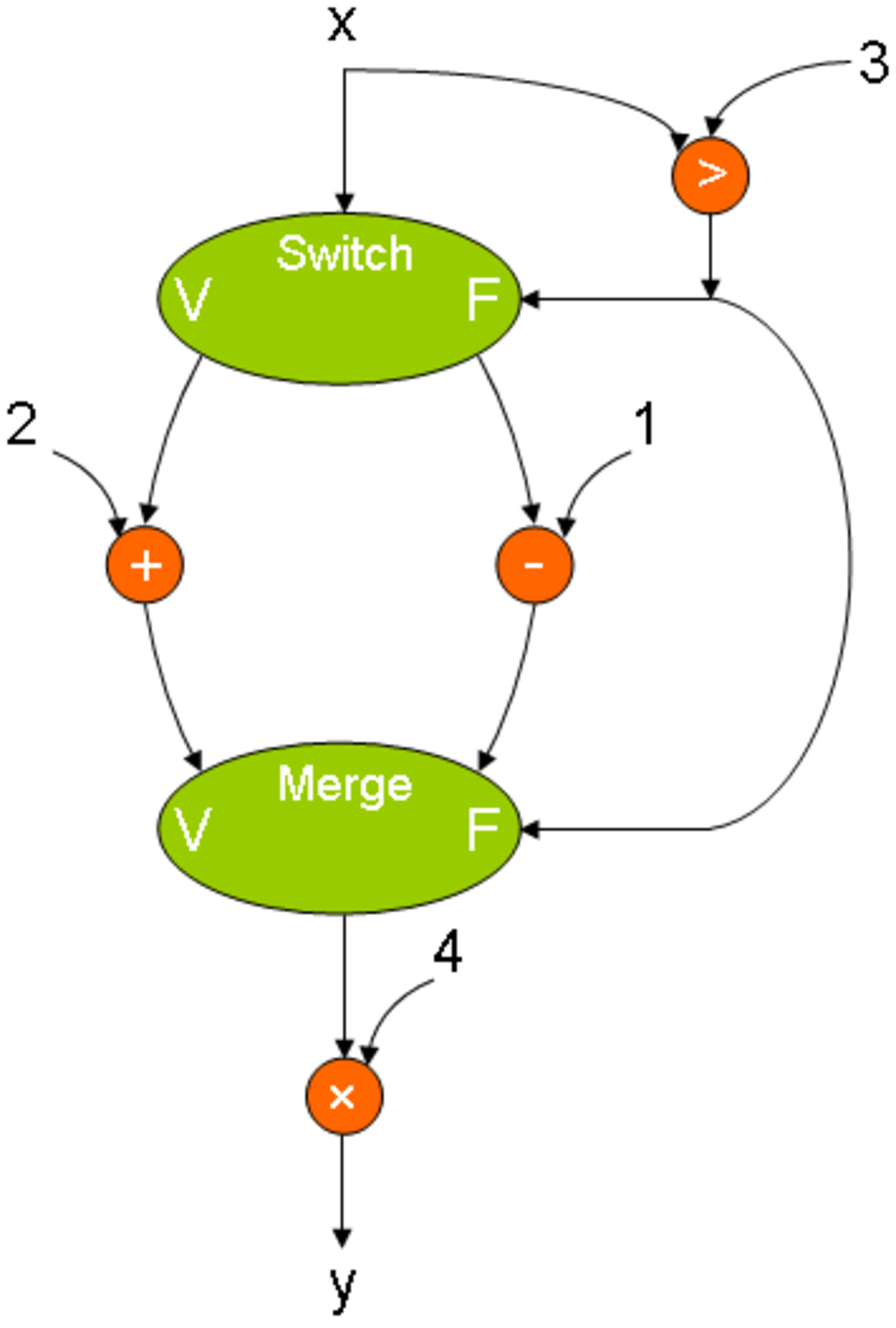
Voici deux exemples de ces instructions, dans un test conditionnel et dans une boucle. Notez l'initialisation à Faux sur le nœud merge pour correctement sélectionner la valeur de x.

Le graphe du programme y = (IF x > 3 THEN x + 2 ELSE x -1) × 4.

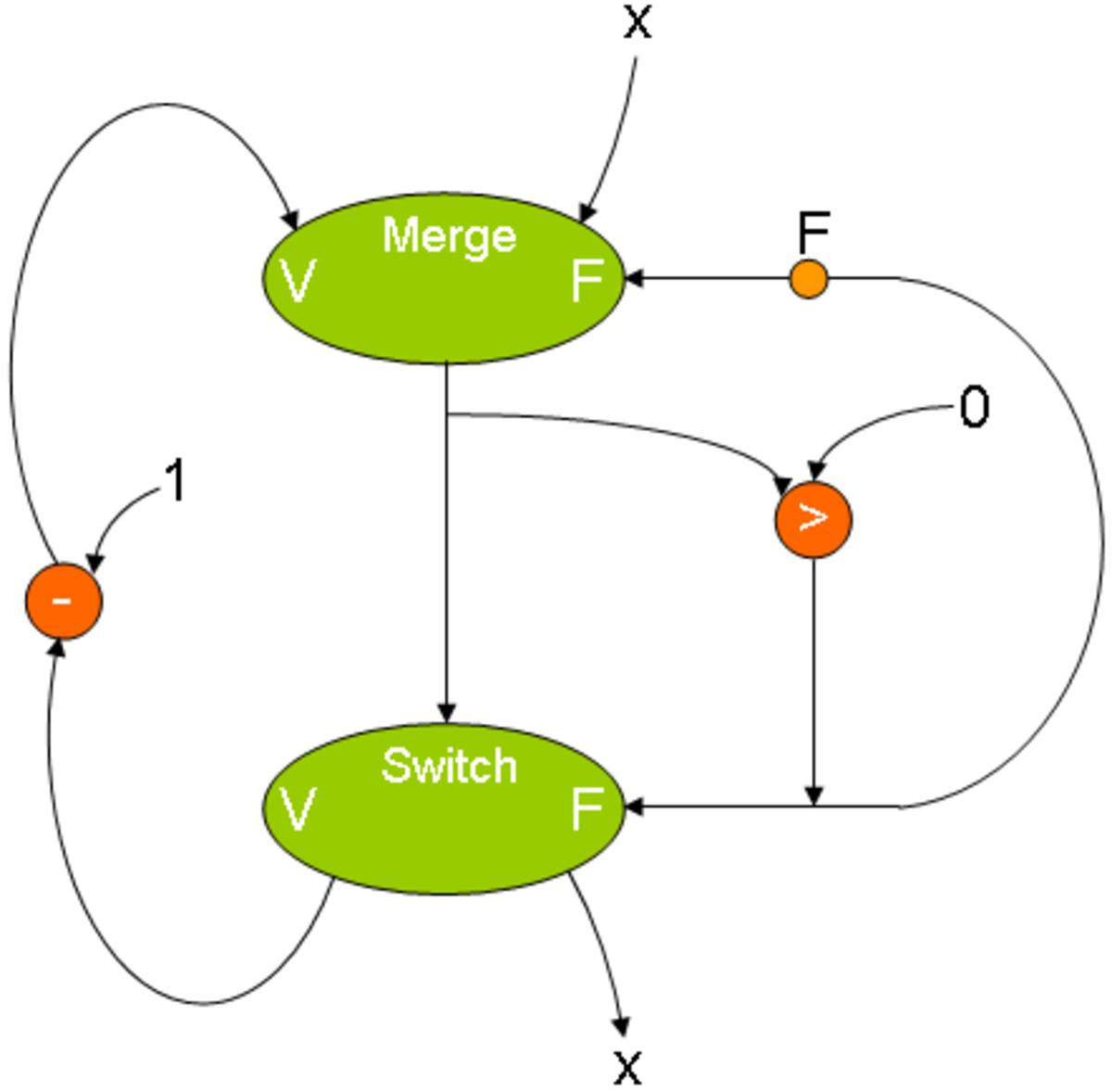
Le graphe du programme WHILE x > 0 DO x - 1.

Implications de l'utilisation de graphes

1. localité : les interdépendances entre les données sont très localisées, contrairement aux langages impératifs habituels qui utilisent des variables globales (situées « loin » des procédures qui sont susceptibles de les modifier).
2. pas d'effets de bord, pas de notion de passage de paramètres par référence : les valeurs sont dupliquées.
3. Dépliage des boucles : pour paralléliser l'exécution des boucles, le code doit être déplié pour que chaque itération puisse être exécutées en parallèle.
4. règle de la référence unique :

le nom d'une variable ne peut apparaître qu'une seule fois dans une assignation. Pour éviter cela, on renomme la variable à partir de ce point, et on utilise ce nouveau nom par la suite. Par exemple :

Cette règle a été proposée en 1968.