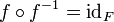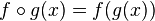Application (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Injectivité et surjectivité
- Une application f de E dans F est dite injective, ou encore une injection lorsque tout élément de l'ensemble d'arrivée de f a au plus un antécédent dans l'ensemble de départ par f, ce qui peut s'écrire :
-
![\forall x_1,x_2\in E \left[ f(x_1)=f(x_2)\Rightarrow x_1=x_2\right]](https://static.techno-science.net/illustration/Definitions/autres/2/2586d1895f4eab8138e7e958d2df78cb_37002895e2c50192da9ff770799aee0e.png)
- ou encore par contraposée :
-
![\forall x_1,x_2\in E \left[ x_1\neq x_2\Rightarrow f(x_1)\neq f(x_2)\right]](https://static.techno-science.net/illustration/Definitions/autres/4/4d67e0535886937cfe244068b33694e8_28fecdb0f4e176e5db3c7023c0603e22.png)
![\forall x_1,x_2\in E \left[ f(x_1)=f(x_2)\Rightarrow x_1=x_2\right]](https://static.techno-science.net/illustrationWebp/Definitions/autres/2/2586d1895f4eab8138e7e958d2df78cb_37002895e2c50192da9ff770799aee0e.png)
![\forall x_1,x_2\in E \left[ x_1\neq x_2\Rightarrow f(x_1)\neq f(x_2)\right]](https://static.techno-science.net/illustrationWebp/Definitions/autres/4/4d67e0535886937cfe244068b33694e8_28fecdb0f4e176e5db3c7023c0603e22.png)
- La composée de deux injections est une injection et, inversement, si pour une certaine fonction g, g o f est une injection, alors f est une injection.
- Une application f de E dans F est dite surjective, ou encore une surjection, lorsque tout élément de l'ensemble d'arrivée est image par f d'au moins un élément de l'ensemble de départ, ce qui s'écrit :
-
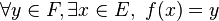
- En d'autres termes, f est surjective ssi son ensemble image est l'ensemble d'arrivée tout entier.
- La composée de deux surjections est une surjection et, inversement, si
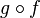
- Une application f est dite bijective, ou que c'est une bijection, lorsqu'elle est à la fois injective et surjective, c'est-à-dire que tout élément de son ensemble d'arrivée a un antécédent et un seul par f dans l'ensemble de départ.
- La composée de deux bijections est une bijection mais inversement, si la composée de deux applications est une bijection, on peut seulement en déduire que l'une est une injection et l'autre une surjection.
Opération sur les applications
- Restriction : soit f une application de E dans F, et soit E’ un sous-ensemble de E. La restriction de f à E’, notée
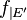
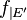
- Corestriction : la corestriction est l'opération analogue sur un sous-ensemble de l'ensemble d'arrivée, mais si on veut que celle-ci reste une application, on ne peut restreindre l'ensemble d'arrivée F de f qu'à un sous-ensemble F’ de F contenant l'ensemble image de f. On obtient alors une application qui a même ensemble de départ et même graphe, mais pas même ensemble d'arrivée.
- Prolongement : soient deux applications f de E dans F de graphe G, et f’ de E’ dans F’ de graphe G’. On dit que f’ est un prolongement de f quand :
- E ⊂ E’ et F ⊂ F’ et G ⊂ G’.
- Composition : la composition de deux applications f de E2 dans E3 et g de E1 dans E2 se note
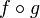
Si le graphe de f est Gf et le graphe de g est Gg, le graphe de
-
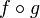
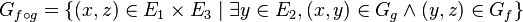
Décomposition canonique
On appelle relation binaire associée canoniquement à l'application f la correspondance
- « x est en relation avec y ssi x et y ont une image commune par f »
Cette relation est toujours symétrique et transitive, du fait de l'unicité de l'image, et est également réflexive du fait de son existence, c'est donc une relation d'équivalence.
Nous pouvons alors définir l'ensemble quotient
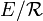
Considérons alors la correspondance i de
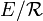
- « A est en relation avec y ssi A est l'ensemble des antécédents de y par f
Cette correspondance est une injection, l'injection canonique associée à l'application f. On montre aisément que
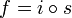
En résumé : Toute application peut être décomposée de façon unique en une surjection et une injection.
Cette décomposition est la décomposition canonique de l'application. Dans cette décomposition :
- la surjection s est une bijection ssi f est une injection, c'est-à-dire si
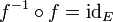
- l'injection i est une bijection ssi f est une surjection, c'est-à-dire si
