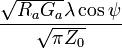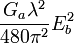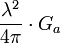Antenne radioélectrique - Définition

Théorie générale

Très généralement, une antenne radioélectrique convertit les grandeurs électriques dans un conducteur ou une ligne de transmission (tension et courant) en grandeurs électromagnétiques dans l'espace (champ électrique et champ magnétique). En émission, la puissance électrique est convertie en puissance électromagnétique et c'est l'inverse en réception.

Fonctionnement en émission

Émission du doublet électrique élémentaire

Schéma géométrique d'une antenne élémentaire.

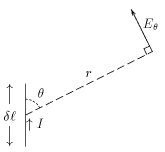
Une antenne élémentaire en émission, dénommée également doublet électrique, est constituée d'une petite longueur de conducteur (petite devant la longueur d'onde ) dans lequel circule un courant alternatif :

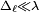
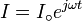
Dans laquelle est la pulsation (et la fréquence). est le nombre imaginaire. (Cette notation, employant les nombres complexes correspond à la notation complexe des impédances).

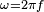
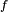
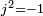
Soit un repère dont l'origine est placée au centre de l'antenne, et dont l'ordonnée se confond avec l'antenne, Le champ créé par cette antenne élémentaire en un point de coordonnées polaires , telle que est:

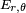
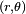
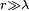
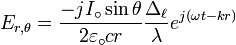
Dans lequel :

• est l'amplitude du champ électrique au point .
• est la permittivité diélectrique du vide.
• est la vitesse de la lumière dans le vide.
• est la distance entre le dipôle et le point où le champ est evalué.
• est le nombre d'onde

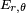
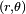
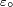
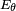
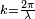
Le champ électrique lointain de l'onde électromagnétique est coplanaire avec le conducteur et perpendiculaire à la ligne qui relie le point où il est évalué au conducteur. Si nous imaginons l'antenne élémentaire au centre d'une sphère et parallèle à l'axe nord-sud, le champ électrique de l'onde électromagnétique rayonnée sera parallèle aux méridiens et le champ magnétique de l'onde aura la même direction que les parallèles géographiques.

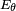
Une telle antenne élémentaire n'existe pas. Une antenne filaire réelle quelconque sera considérée comme constituée par la juxtaposition d'antennes élémentaires, et ses caractéristiques seront obtenues par l'intégration des champs élémentaires, sachant que les caractéristiques du courant dans chaque élément sont différentes en amplitude et en phase. Une antenne cette fois réelle, que l'on peut ainsi construire, est l'antenne doublet demi-onde, encore appelée dipôle demi-onde.

Si P est la puissance rayonnée par l'antenne élémentaire (doublet électrique), le champ électrique rayonné en un point situé à une distance r de cette antenne, est maximum dans une direction perpendiculaire au conducteur de l'antenne (sens du vecteur de Poynting). L'amplitude (maximale) de ce champ est donnée par la relation :

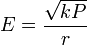
E en V/m; P en W; r en m. Avec k = 90 pour un doublet électrique élémentaire (élément théorique, petit par rapport à la longueur d'onde).

Note: pour certains auteurs, le doublet électrique désigne plutôt le dipôle demi-onde, de longueur égale à la demi-onde.

Émission de l'antenne isotrope

L'antenne isotrope est une antenne fictive qui rayonnerait le même champ dans toutes les directions. Elle sert de référence pour définir le "gain" des antennes (voir plus loin) La formule précédente s'applique pour trouver l'amplitude maximale du champ E, en faisant k = 60 (on retrouve cette formule en considérant le flux du vecteur de Poynting sur la surface d'une sphère de rayon r).

Si on considère le champ efficace, on fera k = 30.

Émission du dipôle demi-onde

Si on considère l'amplitude maximum du champ E dans une direction médiatrice du dipôle, la formule précédente s'applique en faisant k = 98 (2,15 dB de plus que l'antenne isotrope).

Si on cherche le champ efficace, on fera k = 49

Fonctionnement en réception

Le champ électrique d'une onde électromagnétique induit une tension dans chaque petit segment de tout conducteur électrique. La tension induite dépend de la valeur du champ électrique et de la longueur du segment. Mais la tension dépend aussi de l'orientation du segment par rapport au champ électrique.

Ces petites tensions induisent des courants et ces courants qui circulent traversent chacun une petite partie de l'impédance de l'antenne. Le résultat est que le schéma équivalent de Thévenin d'une antenne n'est pas immédiat à calculer.

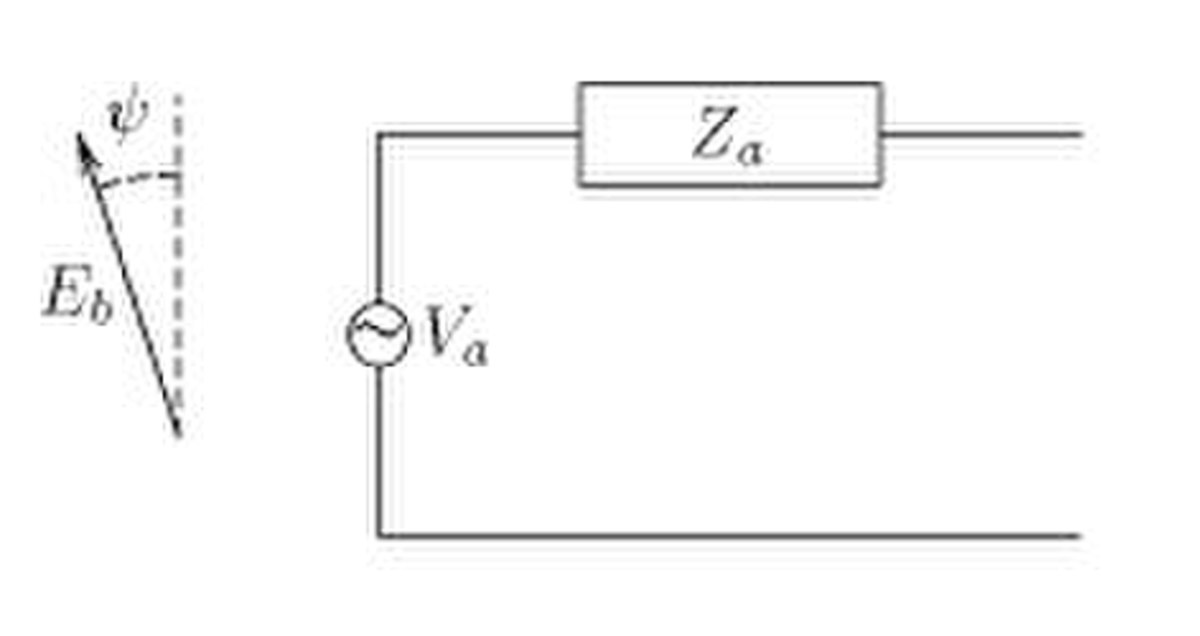
En utilisant le théorème de réciprocité on peut démontrer que le schéma équivalent de Thévenin d'une antenne en réception est le suivant :

Schéma géométrique d'un circuit équivalent.

• est la tension du schéma équivalent de Thévenin.
• est l'impédance intrinsèque du vide.
• est l'impédance du schéma équivalent de Thévenin et est égale à l'impédance de l'antenne.
• est la résistance série de l'impédance de de l'antenne.
• est le gain de l'antenne (le même qu'en émission) dans la direction d'où viennent les ondes électromagnétiques.
• est la longueur d'onde.
• est le champ électrique de l'onde électromagnétique incidente.
• est l'angle de désalignement du champ électrique avec l'antenne. Par exemple, si l'antenne est un dipôle, la tension induite sera maximum quand le champ électrique est aligné avec le conducteur. Si ce n'est pas le cas, et qu'ils forment un angle de , la tension induite sera multipliée par . Cette formule donne donc l'atténuation en fonction de l'angle de dépolarisation.

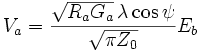
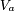
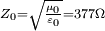
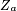
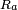
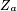
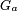
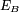
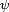
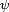
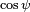
Le schéma équivalent et la formule à droite sont valables pour tout type d'antenne. Ce peut être une antenne dipolaire, une antenne parabolique, une antenne Yagi-Uda ou un réseau d'antennes.

Notions relatives aux antennes réceptrices: les trois définitions suivantes découlent toutes de la formule du paragraphe précédent.

Longueur effective de l'antenne
Puissance maximum disponible
Surface effective ou section efficace