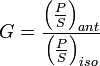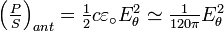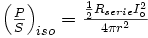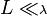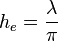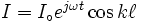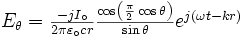Antenne dipolaire - Définition
La liste des auteurs de cet article est disponible ici.
Gain d'une antenne
Le gain d'une antenne est défini comme le rapport des puissances par unité de surface de l'antenne donnée et d'une antenne hypothétique isotrope :
La puissance par unité de surface transportée par une onde électromagnétique est :
La puissance par unité de surface émise par une antenne isotrope alimentée avec la même puissance est:
Les dBi sont les décibels du gain par rapport à une antenne isotrope.
Voici un tableau avec les gains d’antennes dipôlaires en fonction de leur longueur (exprimée en nombre de longueurs d'onde) ; les gains ne sont pas convertis en dBi :
| Longueur en
| Gain | Note |
|---|---|---|
|
| 1,50 | Dipôle court |
| 0,5
| 1,64 | Dipôle demi-onde |
| 1,0
| 1,80 | Dipôle pleine onde |
| 1,5
| 2,00 | |
| 2,0
| 2,30 | |
| 3,0
| 2,80 | |
| 4,0
| 3,50 | |
| 8,0
| 7,10 |
Ces valeurs ont peuvent être obtenues par calcul pour certaines longueurs de dipole comme ci-dessous, sinon interpolées (et confirmées en pratique par la mesure).
Hauteur effective de l'antenne
Lorsque le dipôle baigne dans un champ électrique généré par l'antenne émettrice, une tension est induite dans le circuit connecté à la sortie de l'antenne. Celle-ci s'exprime par :
- V = heEeff
où Eeff est la valeur efficace du champ électrique en V/m auquel est soumis l'antenne et he sa hauteur effective en m, cette dernière étant différente de sa longueur physique. Ainsi pour un dipôle demi-onde :
Dipôle demi-onde
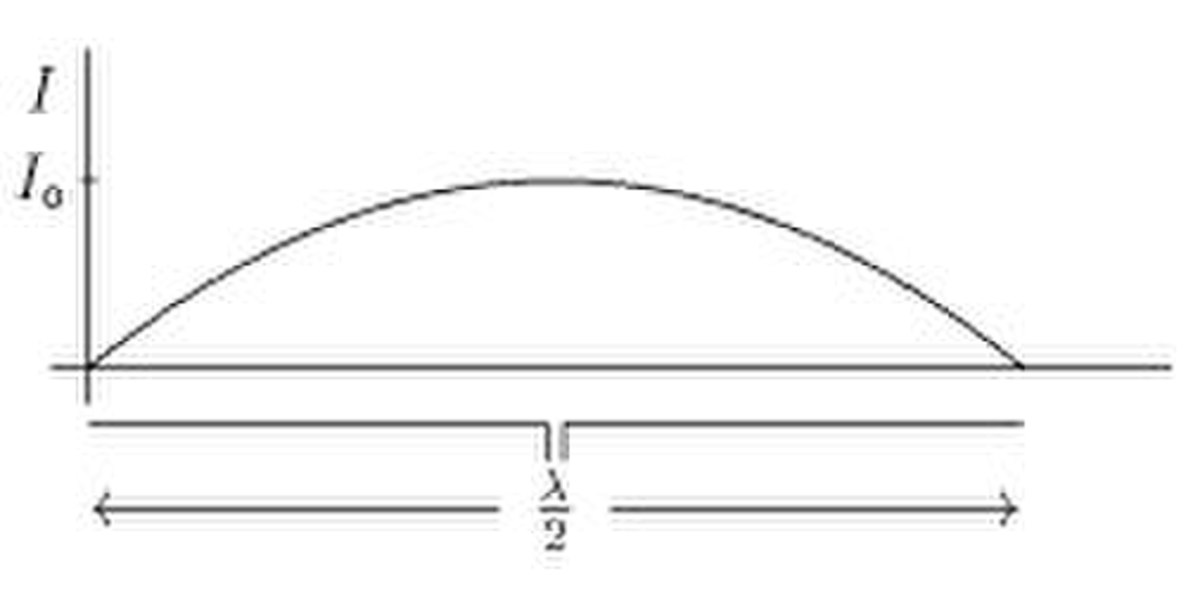
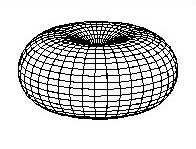
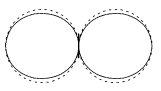
Un dipôle
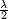
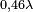
Dans le cas du dipôle
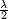
Pour
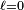
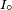
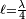
Malgré les simplifications de ce cas particulier, la formule du champ éloigné est difficile à traiter :
Néanmoins, la fraction
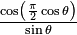
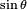
Le résultat est un diagramme d'émission un peu aplati (voir les dessins de droite).
Cette fois nous ne pouvons pas calculer analytiquement la puissance totale émisse par l'antenne. Un calcul numérique simple nous mène à une valeur de résistance série de :
-
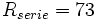
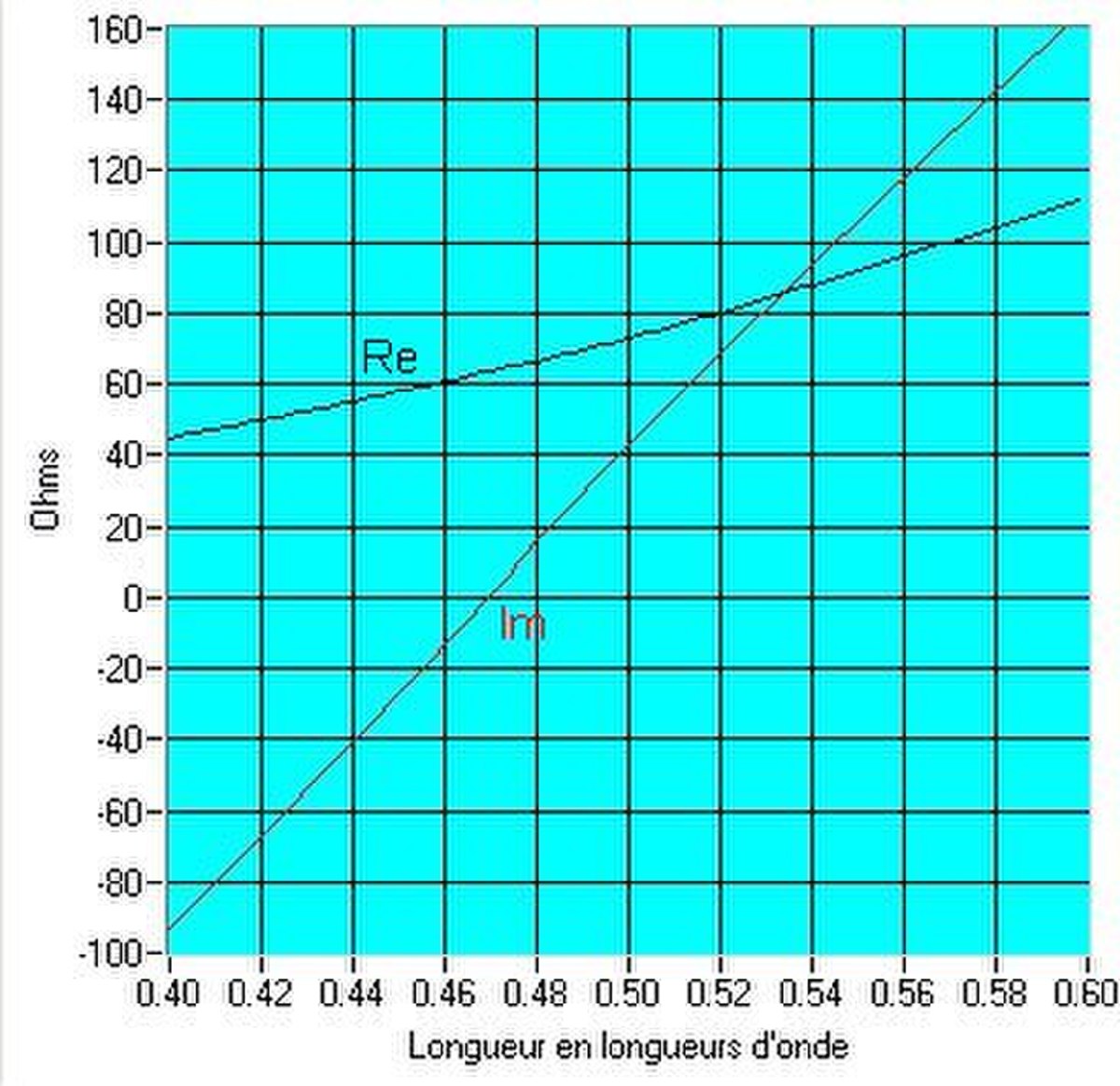
Mais ce n'est pas suffisant pour caractériser l'impédance du dipôle qui comporte aussi une partie imaginaire. Le plus simple c'est de la mesurer. Dans l'image de droite on trouve les parties réelle et imaginaire de l'impédance pour des longueurs de dipôle qui vont de
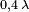
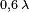
Le gain de cette antenne est :
-
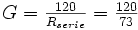
Si la résistance croit assez lentement avec la longueur du dipôle, il n'en est pas de même de la partie imaginaire de l’impédance, responsable du déphasage entre le courant et le champ électrique au centre du dipôle (ou sa tension d'alimentation). L’impédance imaginaire devient nulle et change de signe lorsque le dipôle voisine la demi-longueur d’onde (en fait pour un nombre d’onde voisin de 0,47).