Anneau principal - Définition

• L'anneau Z[ω] est principal :

L'analyse du groupe des classes d'idéaux montre que s'il existe des idéaux non principaux de Z[ω], alors il en existe un de norme inférieure ou égal à 2.√19 / π (cf l'article Entier quadratique). La norme d'un idéal J est égal au cardinal de l'anneau Z[ω] / J. Comme 2.√19 / π est inférieur à 2,8, il suffit de montrer qu'il n'existe aucun idéal J tel que Z[ω] / J soit isomorphe à Z/2Z.

Soit J un idéal de norme deux, le morphisme canonique de Z[ω] dans Z[ω] / J induit un morphisme φ de Z[ω] dans Z/2Z. Tout idéal de norme égale à deux est le noyau d'un tel morphisme. Déterminons l'image de ω par φ. On remarque que ω² - ω + 5 est égal à 0. On en déduit :

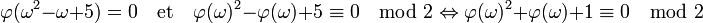
Or dans Z/2Z le polynôme X² + X + 1 est irréductible, c'est-à-dire qu'il n'admet pas de racine. Il n'existe donc pas d'idéal de Z[ω] de norme égale à deux. S'il existait dans Z[ω] un idéal non principal, alors il existerait un idéal non principal de norme égal à deux. Or, il n'existe aucun idéal de norme égal à deux, ce qui montre que l'anneau Z[ω] est principal.

• Le groupe des unités de Z[ω] contient deux éléments 1 et -1 :

Le groupe des unités d'un anneau unitaire désigne l'ensemble des éléments inversibles, encore appelés unités, de l'anneau. Cet ensemble forme un groupe pour la multiplication. Soit z un élément non nul de Z[ω], il existe deux entiers relatifs a et b tel que z = a + b.ω (cf l'article Entier quadratique). Le carré du module de z est un entier strictement positif égal à a² + a.b + 5b². Si z⁻¹ est élément de Z[ω] alors son module est un entier strictement positif et comme le produit des modules de z et z⁻¹ est égal à 1 et que le carré du module de z⁻¹ est égal à l'inverse du carré du module de z, le module de z est nécessairement égal à un. La valeur de b est donc égal à zéro et celle de a à un en valeur absolue, ce qui montre la proposition.

• Il n'existe pas d'idéal non nul J tel que Z[ω] / J contienne strictement moins que quatre éléments :

On a déjà démontré que si J est un idéal non nul de Z[ω], Z[ω] / J n'est pas de cardinal deux, il suffit donc de démontrer que le quotient ne peut contenir trois éléments. Le raisonnement précédent montre qu'un tel quotient n'existe que si le polynôme P[X] suivant dans Z / 3Z admet une racine :

Dans Z / 3Z les seuls carrés sont zéro et un, le polynôme P[X] est irréductible dans Z / 3Z et il n'existe pas de morphisme autre que trivial de Z[ω] dans Z / 3Z. Ceci montre qu'il n'existe pas d'idéal J tel que Z[ω] / J contienne exactement trois éléments et termine la démonstration.

• L'anneau Z[ω] n'est pas euclidien :

Raisonnons par l'absurde, soit δ un stathme euclidien sur Z[ω] - {0}. Il est toujours possible de choisir δ tel que son image soit égal à un pour un élément z de Z[ω] si et seulement si z est inversible. Le stathme ne peut être constant égal à un sur Z[ω] car si tel était le cas, Z[ω] serait un corps (tout élément non nul est inversible), or deux n'est pas inversible dans Z[ω].

Soit z un élément de Z[ω] tel que δ(z) soit la plus petite valeur strictement supérieure à un et atteinte par le stathme. Le reste de la division euclidienne d'un élément quelconque de Z[ω] par z est, soit nulle, soit un élément du groupe des unités. Le quotient Z[ω] / zZ[ω] contient au plus trois éléments : la classe de zéro ou une classe d'un élément du groupe des unités. Comme le seul idéal J de Z[ω] tel que Z[ω] / J contienne strictement moins de quatre éléments est l'idéal trivial {0}, z est donc inversible. La contradiction réside dans le fait que z est un élément inversible tel que δ(z) est strictement supérieur à un. Cette impossibilité termine la démonstration.

Soit J un idéal de A, et (f_i) pour i élément de I une famille génératrice de l'idéal J, composée de fonctions non nulles. La fonction f_i est holomorphe et n'admet qu'un nombre fini de racines à un ordre de multiplicité finie. Il existe donc un polynôme p_i tel que le quotient f_i / p_i soit une fonction de A qui ne s'annule pas sur X. Le quotient est une unité, ce qui montre que la famille de polynômes (p_i) est génératrice de l'idéal J.

Soit M l'idéal de l'ensemble des polynômes à coefficients dans C engendré par la famille (p_i). Cet idéal est principal car l'anneau des polynômes à coefficients dans C l'est. Soit m un polynôme engendrant M. Par définition m est élément de M et donc élément de J. Par construction m engendre p_i et donc f_i. L'idéal engendré par m contient donc J et est contenu dans J, ce qui démontre que J est principal.