Anneau (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Anneaux remarquables
Anneaux de Boole
Un anneau de Boole, noté

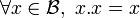
Quelques propriétés des anneaux de Boole :
-

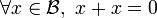
-

-

Exemple : l'ensemble des parties

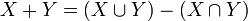
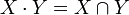
Les notions d'anneau de Boole et d'algèbre de Boole sont intimement liées (voir l'article Algèbre de Boole (structure)).
Anneaux intègres, réduits, factoriels et euclidiens
- Anneau intègre : anneau dans lequel tout élément non nul est régulier i.e. qu'aucun élément n'est un diviseur de zéro. Par définition, tout anneau intègre est unitaire et/ou commutatif.
- Anneau réduit : un anneau est dit réduit si et seulement si son élément nul est le seul élément nilpotent.
-
- Exemple :
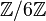
- Exemple :
- Corps : un corps est un anneau unitaire dont tous les éléments non nuls sont inversibles.
-
- Tout anneau intègre fini est nécessairement un corps.
-
- Corps des fractions d'un anneau intègre
-
- Un anneau commutatif unitaire intègre (ou domaine d'intégrité) est presque un corps mais certains éléments ne sont pas toujours inversibles. On démontre que l'on peut plonger tout anneau commutatif intègre dans un corps appelé corps des fractions de A.
- Remarque : il n'est pas nécessaire que l'anneau soit unitaire, car l'élément neutre apparaît de toute façon dans la construction du corps des fractions.
- Anneau factoriel : anneau commutatif unitaire intègre dans lequel tous les éléments se décomposent de manière unique (aux inversibles près) en produit d'éléments irréductibles.
-
- plus exactement pour tout a de A, il existe n éléments irréductibles p1, p2, ..., pn tels que a = p1p2...pn. Cette décomposition est unique à l'ordre des pi près et au produit par des éléments inversibles près.
- Anneau euclidien : anneau commutatif unitaire intègre dans lequel on peut définir une division euclidienne.
-
- Plus précisément, il existe une application v (appelé stathme euclidien) de A\{0} dans N telle que pour tout a et b de A, b non nul, il existe un couple (q, r) de A2 tel que a = bq + r avec r nul ou v(r) < v(b)
-
-
![\mathbb Z[i]](https://static.techno-science.net/illustration/Definitions/autres/e/e2abb021e74e2b38379dfefd04b2b086_b9c67de2e72b9a3319ad0e164884ee55.png)
- L'anneau
- Si

![\mathbb K[X]](https://static.techno-science.net/illustration/Definitions/autres/1/11cf18672fa8c102e5d2ec8bdfe203c8_bd379140d6a603f16bfb95868779a783.png)
-
Idéaux d'un anneau
Plus intéressante que la structure de sous-anneau, la structure d'idéal s'apparente à celle de sous-groupe distingué dans un groupe.
Un idéal I (à droite ou à gauche) est un sous-groupe additif de A vérifiant
- pour tout x de I et tout a de A, ax ∈ I pour un idéal à droite
- pour tout x de I et tout a de A, xa ∈ I pour un idéal à gauche
Un idéal à droite et à gauche est appelé idéal bilatère.
Exemples
- {0} est un idéal bilatère de tout anneau, l'idéal nul.
- A est un idéal bilatère de A.
- Si a a un élément de l'anneau A, l'ensemble des multiples à droite de a (les éléments de la forme ax) est un idéal à droite de A. Il est noté (a).
- L'intersection de deux idéaux (resp. à gauche, resp. à droite) de A est un idéal de A (resp. à gauche, resp. à droite).
Anneaux quotients
Un idéal bilatère permet de créer un anneau quotient : le groupe quotient commutatif A/I peut être muni d'une multiplication associative et distributive par rapport à l'addtion, et donc d'une structure d'anneau.
Anneaux commutatifs définis par une propriété de leurs idéaux
Selon les propriétés des idéaux d'un anneau A, on distingue des familles d'anneaux particuliers:
- Anneau principal : anneau commutatif unitaire intègre dont tous les idéaux sont principaux.
-
- Voir article détaillé : Anneau principal
- Un anneau euclidien est principal
- Un anneau principal est factoriel
- Anneau noethérien : anneau commutatif unitaire dont les idéaux sont engendrés par un nombre fini d'éléments
-
- Voir article détaillé : Anneau noethérien
- Anneau artinien : anneau commutatif unitaire dont toute suite d'idéaux décroissante (pour l'inclusion) est stationnaire.
-
- Voir article détaillé : Anneau artinien
- Anneau local : anneau commutatif unitaire dans lequel il n'existe qu'un seul idéal maximal.
- Anneau de Bézout : Anneau commutatif unitaire intègre dans lequel tout idéal de type fini est principal
- Anneau de Dedekind : Anneau noethérien intégralement clos dans lequel tout idéal premier non nul est maximal.
-
- Voir article détaillé : Anneau de Dedekind

















































