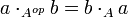Anneau (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Exemples
- L'ensemble des entiers relatifs,
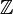
- L'ensemble des entiers congruents modulo un nombre entier donné p est un anneau commutatif unitaire pour la loi provenant la congruence ; il est noté
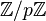
- Ainsi
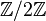
- Un pair plus un pair est pair (0+0=0).
- Un impair plus un pair est impair (0+1=1+0=1).
- Un impair plus un impair est pair (1+1=0).
- Un pair fois un entier quelconque est pair (0*x=0).
- Un impair fois un impair est impair (1*1=1).
- Un corps est un cas particulier d'anneau (unitaire) pour lequel tous les éléments non nuls sont inversibles pour la loi (.).
- En particulier, l'ensemble des nombres rationnels,



- L'ensemble des nombres décimaux,
- L'ensemble des réels s'écrivant
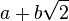
- En particulier, l'ensemble des nombres rationnels,
- Les endomorphismes d'un espace vectoriel (applications linéaires de l'espace vers lui-même) forment un anneau, avec l'addition de fonction pour la loi +, et la composition pour la loi ∙. L'identité est un élément neutre pour ∙, donc c'est un anneau unitaire. Il n'est pas commutatif en général. C'est une grande source de contre-exemples à des affirmations fausses sur les anneaux.
- Plus généralement les endomorphismes d'un groupe abélien forment un anneau.
- L'ensemble des matrices 2 × 2, à coefficients réels, muni de l'addition et de la multiplication est aussi un anneau non commutatif unitaire, isomorphe à l'anneau des endomorphismes de l'espace vectoriel
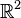
- L'ensemble des polynômes à coefficients dans un anneau commutatif est aussi un anneau commutatif.
- L'ensemble des applications d'un ensemble X à valeurs dans un anneau, muni des lois héritées de l'anneau (c'est-à-dire (f+g)(x)=f(x)+g(x) et (f*g)(x)=f(x)*g(x)) forme un anneau noté AX.
Anneau nul
L'ensemble à un seul élément {0} muni des opérations 0+0=0 et 0.0=0 est un anneau, appelé anneau nul.
La notion de pseudo-anneau de carré nul est plus intéressante : on dit qu'un pseudo-anneau A est de carré nul si le produit de deux éléments de A est toujours nul. Si le pseudo-anneau est unitaire, il est alors réduit à 0 car pour tout élément x de A, on a : x=1.x=0. Tout groupe abélien (A, +) peut être muni d'une structure de pseudo-anneau nul en posant x.y=0.
Anneau opposé
L'anneau opposé Aop d'un anneau A possède le même groupe additif sous-jacent que A et sa multiplication est effectuée dans l'ordre opposé : si l'on note
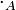
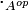
Il est clair que si A est commutatif, A = Aop.
Sous-anneaux
Une partie B d'un anneau A est un sous-anneau de (A, +, .) si :
- (B, +) est un sous-groupe de (A,+)
- B est stable pour la loi .
- S'il est requis que les anneaux soient unitaires (cela dépendant de la définition utilisée), alors le sous anneau doit lui être aussi unitaire et son 1 doit provenir du 1 de l'anneau initial (1A = 1B), ce qui équivaut à
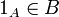
- Un sous-anneau B est un anneau pour les opérations + et . restreintes à B.
Exemples
Dans le cas unitaire
- Dans l'anneau commutatif (unitaire) Z, 2 Z est un idéal, qui n'a pas d'élément unité, ce n'est donc pas un anneau et encore moins un sous-anneau de Z.
- Dans l'ensemble des matrices carrées M2 (à coefficients dans R par exemple), anneau non-commutatif unitaire, l'ensemble des matrices de la forme :
-
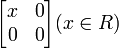


Dans le cas non-unitaire
- 2 Z est cette fois-ci un (pseudo-)anneau et c'est bien un sous anneau de Z.
-
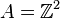
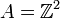
Construction de sous-anneaux
- Éléments entiers sur un sous-anneau B : dans un anneau commutatif unitaire intègre A contenant un sous-anneau B, un élément x ∈ A est entier sur B si et seulement si x est solution d'une équation P(x) = 0 où P est un polynôme unitaire à coefficient dans B.
-
- L'anneau Z des entiers relatifs est un sous-anneau de l'anneau Q des rationnels. Les seuls éléments de Q entiers sur Z sont les entiers relatifs.
- L'anneau Z des entiers relatifs est un sous-anneau de l'anneau Q[i] des complexes s'écrivant a + ib, a et b étant des rationnels . Les éléments de Q[i] entiers sur Z sont les complexes s'écrivant a + ib, a et b étant des entiers relatifs.
- Fermeture intégrale d'un sous-anneau B : dans un anneau commutatif unitaire intègre A contenant un sous-anneau B, la fermeture intégrale de B dans A est l'ensemble des éléments de A entiers sur B. C'est un sous-anneau de A contenant B comme sous-anneau.
Un anneau intégralement clos est un anneau commutatif unitaire intègre égal à sa fermeture intégrale dans son corps des fractions.
-
- L'anneau des entiers relatifs est intégralement clos.
- Plus généralement : un anneau factoriel est intégralement clos.
- Le centre Z(A) d'un anneau A est par définition Z(A)={x∈A / ∀y∈A, x.y=y.x}, c’est-à-dire l'ensemble des éléments qui commutent avec tous les autres pour la loi ".". C'est un sous-anneau.
- L'intersection de deux sous-anneaux d'un même anneau, est un sous-anneau.
- L'image d'un anneau par un homomorphisme d'anneau est un sous-anneau de l'anneau d'arrivée. (Si les anneaux sont unitaires, on impose aux morphismes de transformer unité en unité.)
Cependant, la structure de sous-anneau (excepté le cas d'un anneau dans son corps des fractions) est moins riche en résultats que celle d'idéal ou de module sur un anneau.