Anneau (mathématiques) - Définition

Définitions

Un anneau est un triplet (A, +, ∙) tel que :

• A est un ensemble ;
• + est une loi de composition interne telle que (A, +) soit un groupe commutatif ; ce qui signifie que
  • la loi + est associative ;
  • A contient au moins un élément : l'élément neutre pour la loi +, noté 0 ;
  • tout élément a de A a un opposé, noté −a ;
  • la loi + est commutative (a+b = b+a) ;
• ∙ est une loi de composition interne associative et distributive par rapport à + ;

Depuis les années 1960, Nicolas Bourbaki et de nombreux auteurs imposent dans leur définition à un anneau d'être unifère (on dit aussi unitaire), c'est-à-dire que la loi associative . admet un élément neutre noté 1 ou 1_A qui vérifie :

• 1.x = x.1 = x
• Anneau unitaire : un anneau est dit unitaire si la loi ∙ dispose d'un élément neutre, noté 1.

En terminologie universitaire française et en terminologie anglaise les anneaux sont souvent considérés par défaut comme unitaires. Dans le cas contraire, si la loi ∙ ne dispose pas d'élément neutre, on dit que A est un pseudo-anneau ou une algèbre associative. Cependant, comme les auteurs pour qui un anneau n'est pas nécessairement unitaire restent nombreux, il convient d'une part de toujours s'assurer de la définition concrètement utilisée, et il n'est pas inutile d'ajouter l'adjectif "unitaire" même si ce serait redondant. Si A est un pseudo-anneau non unitaire, on peut construire un anneau unitaire A' qui contient A comme sous-anneau non unitaire.

Les auteurs qui supposent les anneaux unitaires imposent aux sous-anneaux de contenir l'unité de l'anneau et aux morphismes d'anneaux : A B, de transformer l'unité de A en l'unité de B. Cette définition (les anneaux sont supposés unitaires) est récente et n'était pas adoptée à l'origine.

Un morphisme d'anneaux est une application entre deux anneaux A et B, compatible avec les lois de ces anneaux, c'est-à-dire qui vérifie :

f(a+b)=f(a)+f(b)

f(a.b)=f(a).f(b)

Si on suppose dans la définition que les anneaux sont unitaires, l'application f doit transformer l'unité de l'anneau unitaire A en l'unité de B.

f(1_A) = 1_B

Si f est une bijection, on dit que f est un isomorphisme d'anneaux.

On dit que deux anneaux A et B sont isomorphes si il existe un isomorphisme de A sur B.

Éléments remarquables d'un anneau

• Élément inversible : un élément a ∈ A d'un anneau unitaire est dit inversible lorsqu'il existe un élément b de l'anneau tels que

a∙b = b∙a = 1. On appelle parfois les éléments inversibles les éléments unités (ou simplement unités). On note l'ensemble des inversibles : A^*.

Voir article détaillé : Élément inversible

Les éléments inversibles de Z sont -1 et 1

• Élément régulier : un élément a ∈ A est dit régulier à droite (resp. à gauche) si et seulement si le seul élément x de A tel que x∙a = 0 (resp. a∙x=0) est x = 0; on note l'ensemble des réguliers : A^×

Un élément inversible est nécessairement régulier mais la réciproque est fausse.

• Diviseur de zéro : un élément non nul a ∈ A est un diviseur de 0 à droite (resp. à gauche) s'il existe un élément b de A non nul et tel que b∙a = 0 (resp. a∙b = 0). Si un anneau commutatif est sans diviseur de 0, on dit qu'il est intègre.

L'ensemble des éléments réguliers et des diviseurs de zéro forment une partition de A\ {0}

Voir article détaillé : Diviseur de zéro

• Élément nilpotent : un élément a ∈ A est dit nilpotent d'ordre n s'il existe un entier n non nul tel que aⁿ=0 et que pour tout k appartenant à {0;n-1} . Si un anneau est sans élément nilpotent, on dit qu'il est réduit.

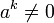
Un élément nilpotent non nul est un diviseur de zéro.

2 est nilpotent dans tous les anneaux où n≥2.

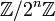
Si a est nilpotent (et l'anneau est unitaire), (1-a) est inversible

• Élément central : un élément qui commute (pour la multiplication) avec tout autre élément de A.

• Élément idempotent ou projecteur : un élément a ∈ A est appelé projecteur ou idempotent lorsque a∙a = a² = a.

Toute projection sur un sous-espace vectoriel est un projecteur dans l'anneau des endomorphismes décrit ci-dessus.

• Diviseur : si a ∈ A est non nul, et d ∈ A. On dit que d est un diviseur de a à droite (resp. à gauche) si et seulement s'il existe b ∈ A tel que a = b∙d (resp. a = d∙b). Si l'anneau est commutatif, on parle simplement de diviseur.

Divisibilité dans un anneau commutatif

• Éléments associés : dans un anneau commutatif unitaire, deux éléments a et b sont associés si il existe un élément inversible u tel que a = u∙b, ce qui équivaut, si l'anneau est intègre, à : a divise b et b divise a.

• Élément irréductible : Dans un anneau commutatif unitaire, un élément a ∈ A non inversible est irréductible si et seulement si ses seuls diviseurs dans A sont les éléments inversibles u ou les éléments s'écrivant a∙u (éléments associés à u).

• Élément premier : Dans un anneau commutatif unitaire, un élément p ∈ A est dit premier si, pour tous éléments a et b de A, si p divise a∙b et si p ne divise pas a alors p divise b

Dans un anneau commutatif unitaire intègre, un élément premier est irréductible, mais la réciproque n'est pas toujours vraie.

• Élément extrémal : Dans un anneau commutatif unitaire, un élément non inversible p ∈ A est dit extrémal si tout élément a de A, non divisible par p, est étranger avec p, c'est-à-dire que il existe deux éléments de A : u et v, tels que au+pv=1. En termes d'idéaux (voir plus loin), cela signifie que l'idéal des multiples de p : (p) est un idéal maximal de A (ce qui équivaut à l'importante propriété : "A / (p) est un corps".)

Dans un anneau commutatif unitaire intègre, un élément maximal est premier, mais la réciproque n'est pas toujours vraie.

• Éléments premiers entre eux : dans un anneau commutatif unitaire intègre, deux éléments a et b sont premiers entre eux si et seulement si, pour tout d de A, si d divise a et d divise b alors d est un élément inversible.