Anneau Z/nZ - Définition

Propriétés

Propriétés élémentaires

La théorie des anneaux permet directement de démontrer certaines propriétés de l'anneau.

• L'anneau Z/nZ est unitaire.

C'est une conséquence directe du fait que Z l'est.

• L'anneau Z/nZ est principal et de Bézout.

Un anneau est principal si et seulement si tous ses ideaux sont principaux. Si un anneau est principal, son quotient par un idéal est aussi principal, or Z est un anneau principal. En pratique et comme pour Z, tous les sous-groupes additifs et tous les sous-anneaux sont aussi des idéaux principaux. Si m est un diviseur de n alors il existe un unique ideal de Z/nZ isomorphe à Z/mZ, ce résultat est une conséquence directe de la troisième proposition du paragraphe Théorème fondamental de l'article groupe cyclique.

Un anneau est dit de Bézout si et seulement si pour tout élément a et b n'ayant comme diviseurs communs que les éléments inversibles, il existe deux éléments α et β tel que α.a + β.b = 1. Z/nZ est un anneau de Bézout car tout anneau principal l'est.

Si n n'est pas premier, alors l'anneau Z/nZ n'est pas intègre, il n'est donc ni euclidien ni factoriel.

Structure additive

La structure du groupe (Z/nZ) est celle d'un groupe monogène, c'est-à-dire engendré par un unique élément. Si n est égal à 0 on obtient un groupe isomorphe à Z et à n'importe quel groupe monogène d'ordre infini.

Si n est différent de 0, alors le groupe est cyclique, sa structure est explicitée dans l'article détaillé.

Théorème chinois

La logique du théorème chinois s'applique encore, ainsi les propriétés du paragraphe Théorème chinois de l'article Groupe cyclique s'appliquent encore. Il suffit pour les vérifier de valider que le morphisme de groupe utilisé est aussi un morphisme d'anneau.

• Soit u et v deux entiers premiers entre eux, alors l'anneau Z/u.vZ est isomorphe au produit des anneaux d'ordre Z/uZ et Z/vZ.

Note : Si u et v ne sont pas premiers entre eux, alors l'anneau produit ne contient pas d'élément d'ordre supérieur au ppcm de u et de v. Cet anneau n'est donc pas isomorphe à l'anneau Z/u.vZ.

Cette proposition entraîne une décomposition unique de Z/nZ en facteurs premiers. Le théorème fondamental de l'arithmétique montre que n se décompose de la manière unique suivante:

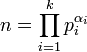
Ou (p_i) est une famille de k nombres premiers tous distincts et α_i des entiers supérieurs ou égaux à un. Les puissances des nombres premiers du produit sont tous premiers entre eux. Une simple récurrence montre :

• Z/nZ se décompose de manière unique en un produit de d'anneaux quotients de Z de cardinal une puissance d'un nombre premier.

Cas où Z/nZ est un corps

• Z/nZ est un corps si et seulement si n est un nombre premier.

En effet, cette proposition est une conséquence directe de l'identité de Bézout. Supposons n premier, alors si a est un entier premier avec n, c'est-à-dire non multiple de n, il existe deux entiers b et c tel que :

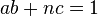
Ce qui signifie que la classe de a est inversible d'inverse la classe de b.

Réciproquement si n n'est pas premier, il existe deux entiers a et b différents de n et de 1 tel que leur produit est égal à n. La classe de a ainsi que la classe de b sont des diviseurs de zéro, ce qui n'existe pas dans un corps.

Caractéristique d'un anneau

Soit A un anneau unitaire, il existe un unique morphisme d'anneau φ de Z dans A qui à 1_Z associe 1_A. Soit n l'entier positif tel que le noyau de φ soit égal à nZ. La décomposition canonique de φ (cf le paragraphe Morphisme d'anneau de l'article Idéal) montre qu'il existe un sous-anneau de A isomorphe à Z/nZ.

• L'entier n est appelé caractéristique de l'anneau A.

Ainsi, tout anneau unitaire contient un sous-anneau isomorphe soit à Z dans le cas où n est égal à 0, soit à Z/nZ. C'est une des raisons qui rend cette famille d'anneau intéressante.