Analyse vectorielle - Définition
La liste des auteurs de cet article est disponible ici.
Opérateurs d'ordre supérieur
Le laplacien
Le plus utilisé des opérateurs d'ordre 2 est le laplacien, du nom du mathématicien Pierre-Simon Laplace. Le laplacien d'un champ est égal à la somme des dérivées secondes de ce champ par rapport à chacune des variables.
En dimension 3 et en coordonnées cartésiennes, il s'écrit :
-
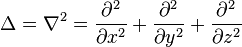
Cette définition a un sens aussi bien pour un champ de scalaires que pour un champ de vecteurs. On parle respectivement de laplacien scalaire et de laplacien vectoriel. Le laplacien scalaire d'un champ de scalaires est un champ de scalaires alors que le laplacien vectoriel d'un champ de vecteurs est un champ de vecteurs. Pour distinguer ce dernier, on le note parfois
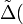
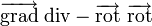
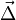
L'autre notation du laplacien qui apparaît ci-dessus,
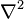

Le laplacien apparaît dans l'écriture de plusieurs équations aux dérivées partielles qui jouent un rôle fondamental en physique.
- La plus simple est l'équation de Laplace Δf = 0. Ses solutions (de classe
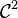
- Le laplacien sert aussi à écrire:
l'équation de Poisson:
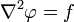
ou encore l'équation des cordes vibrantes :
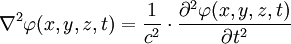
Le laplacien vectoriel
Le Laplacien d'un champ de vecteurs
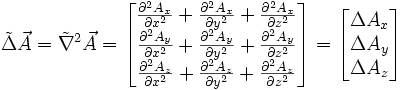
Le Laplacien vectoriel est présent :
- dans l'Équation de Poisson pour les versions vectorielles
- en mécanique des fluides visqueux où il apparait dans les Équations de Navier-Stokes
Application linéaire tangente d'un champ de vecteurs
Soit M' le point translaté de M par la translation de vecteur
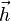
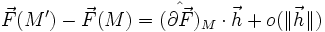
définit l'opérateur linéaire noté par un chapeau pour signifier que sa représentation dans une base est une matrice carrée [3-3], application linéaire tangente du champ de vecteurs F(M).
Le déterminant de cet opérateur est le Jacobien de la transformation qui à M associe F(M).
Sa trace définira ( voir ci-après) la divergence du champ de vecteurs F(M).
Cela permettra de donner du rotationnel du champ de vecteurs F(M) une définition intrinsèque.
On pourra vérifier que symboliquement :
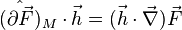
La divergence
La divergence s'applique à un champ de tenseurs d'ordre n et le transforme en un champ de tenseurs d'ordre n-1. Pratiquement, la divergence d'un champ de vecteurs exprime sa tendance à fluer localement hors d'un petit volume entourant le point M où est calculée la divergence.
En dimension 3 et en coordonnées cartésiennes, si
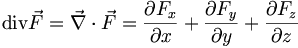
où
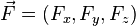
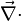
La définition indépendante du choix de la base est :
Une autre définition possible, plus générale mais plus difficile à formaliser, consiste à définir la divergence d'un champ de vecteurs en un point comme le flux local du champ autour de ce point.
Le rotationnel
Le rotationnel transforme un champ de vecteurs en un autre champ de vecteurs. Plus difficile à se représenter aussi précisément que le gradient et la divergence, il exprime la tendance qu'a un champ à tourner autour d'un point : sa circulation locale sur un petit lacet entourant le point M est non nulle. Par exemple :
- dans une tornade, le vent tourne autour de l'œil du cyclone et le champ de vecteurs vitesse du vent a un rotationnel non nul autour de l'œil. Le rotationnel de ce champ de vitesse (autrement dit le champ de vorticité ou encore champ tourbillon) est d'autant plus intense que l'on est proche de l'oeil.
- le rotationnel du champ des vitesses d'un solide qui tourne à vitesse constante est constant, dirigé selon l'axe de rotation et orienté de telle sorte que la rotation ait lieu, par rapport à lui, dans le sens direct et vaut simplement
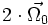
Dans un espace à 3 dimension et en coordonnées cartésiennes, on peut définir le rotationnel par la relation
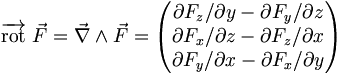
où
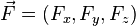
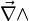
Cela peut aussi s'écrire, par abus de notation, à l'aide d'un déterminant :
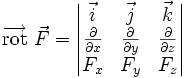
où
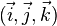
- Une définition intrinsèque (parmi d'autres) du rotationnel est la suivante :
A partir du champ
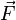
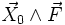
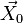
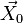
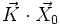
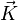
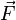
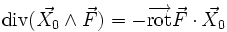
Une autre définition possible, plus générale mais plus difficile à formaliser, consiste à définir le rotationnel d'un champ de vecteurs en un point comme la circulation locale du champ autour de ce point (voir rotationnel en physique).