Analyse spectrale - Définition

Signaux transitoires

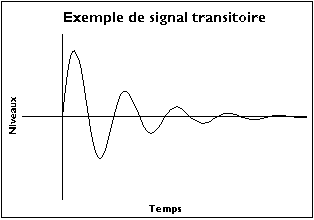
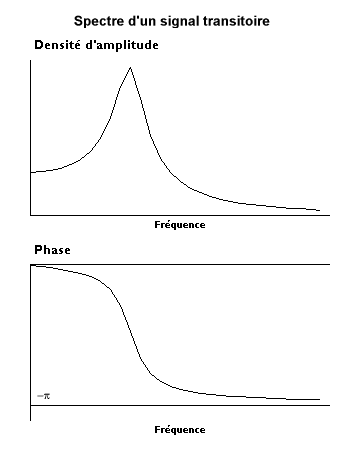
Ici, on raisonnera d'abord sur le signal de durée supposée infinie avant de voir les conséquences pour un enregistrement de durée finie. Si ce signal n'est pas périodique, n'a pas de période finie, on peut essayer de voir ce qui se passerait si on lui prêtait une période infinie. Cela entraîne les conséquences suivantes :

• Lorsque la durée d'analyse T tend vers l'infini, le pas de fréquence 1/T tend vers 0 : à la limite on passe d'un spectre discret à un spectre continu.
• Au cours de cette croissance de la durée d'analyse, lorsque celle-ci est multipliée par un nombre n quelconque, le nombre de composantes est multiplié par le même facteur. Pour que le niveau du signal ne soit pas augmenté dans les mêmes proportions il faut que les amplitudes des composantes soient, en gros, divisées par n, ce qui risque de conduire à la limite à des amplitudes nulles. On pare à cette difficulté en multipliant les coefficients de Fourier par la longueur d'analyse ou en les divisant par le pas de fréquence qui tend vers zéro. Ainsi, le spectre continu n'est plus un spectre d'amplitude mais un spectre de densité d'amplitude dont l'unité est unité physique / hertz.
• Malgré ces précautions, la méthode peut diverger. Une condition de convergence est que le signal doit être transitoire : il doit tendre vers 0 lorsque le temps tend vers ±∞.

On obtient ainsi la transformée du signal x(t) que l'on note généralement X(f), f étant la fréquence.

Si on retourne à un enregistrement de durée limitée, il y a deux possibilités :

1. Le signal n'est différent de zéro que pendant une durée limitée : l'analyse pendant cette durée fournit, au moins en principe, un résultat exact permettant de reconstituer le signal par inversion de la transformation.
2. Le signal a des valeurs différentes de zéro pendant une durée supérieure à celle de l'enregistrement : l'imprécision du résultat croît avec la quantité d'information perdue. L'erreur ainsi commise se traduit concrètement par une dispersion de l'énergie correspondant à une fréquence sur les fréquences voisines et mathématiquement par la notion de convolution.