Analyse factorielle des correspondances - Définition

Extension

La technique de l'AFC peut être utilisée pour des tableaux d'un autre type que tableau de contingence. En revanche, son utilisation pour ces tableaux oblige toujours à des adaptations spécifiques au type de tableau. On peut utiliser l'AFC sur des tableaux :

• logiques
• logiques dédoublés
• de notes d'intensité
• de rang
• de mesure
• qualitatifs

Lorsque l'on utilise l'AFC sur des tableaux disjonctifs complet ou de Burt  , on utilise en réalité la méthode de l'analyse des correspondantes multiples (ACM).

La distance χ2

Etudier la liaison entre deux variables qualitatives revient à étudier l'écart entre les données observées et une situation théorique d'indépendance. Cette situation théorique correspond au tableau :

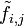
Si le tableau des données vérifie la relation d'indépendance , alors tous les profils-lignes d'une part et tous les profils-colonnes d'autre part sont égaux au profil moyen correspondant.

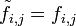
L'écart à l'indépendance est pris en compte en considérant le tableau X de terme général:

,

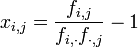
On peut tester l'hypothèse d'indépendance par le test χ² (prononcé "Ki-2")

,

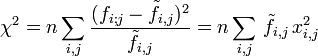
Cette statistique vaut 0 ou proche 0 si les données observées vérifient le modèle d'indépendance. Mais cette statisque ne répond pas aux questions suivantes:

• Par case: quelles sont, entre une modalité ligne i et une modalité colonne j, les associations les plus remarquables?
• Par ligne: quelles sont les départements qui ont un profil de vote particulier?
• Par colonne: quels sont les candidats qui ont un électorat particulier?

Pour répondre à ces questions, on rappelle que l'analyse en composantes principales (ACP) peut réduire la dimension des problèmes et sélectionner les effets principaux. Mais une métrique spéciale est adaptée-la métrique du χ². Dans ce sens, l'AFC peut être considérée comme une ACP particulière dotée de la métrique du χ² qui ne dépend que du profil des colonnes du tableau.

Considérons le tableau X, chaque ligne peut être considéré comme un point dans l'espace de dimension J, noté , dont chaque dimension est associée à une colonne du tableau X. On affecte à la ligne i un poids proportionnel à son effectif soit . Le centre de gravité est confondu avec l'origine des axes :

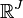
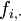
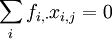
La distance χ² est définie comme (to be continued)

Bibliographie

• Histoire et préhistoire de l'analyse des données, Dunod, 1982, ISBN 2-04-015467-1
• L'analyse des données / lecons sur l'analyse factorielle et la reconnaissance des formes et travaux, Dunod 1982, ISBN 2-04-015515-5
• Linguistique et lexicologie, Dunod, 2007 réédition, ISBN 2-04-010776-2
• Pratique de l'analyse des données, Dunod, 1980, ISBN 2-04-015732-8

• Husson François, Lê Sébastien et Pagès Jérôme ; Analyse de données avec R, Presses Universitaires de Rennes, 2009
• Michel Volle, Analyse des données, Economica, 4^e édition, 1997, ISBN 2-7178-3212-2

• Le Roux B. et Rouanet H., Geometric Data Analysis, Kluwer Academic Publishers, Dordrecht (June 2004)