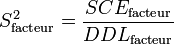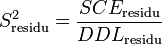Jeudi 1er Mai 2025
Rechercher 🔍

Analyse de la variance - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Principe - Analyse de la variance à deux facteurs - Analyse de la variance à un facteur - Limites d'utilisation de l'analyse de la variance - Analyse de la variance multifactorielle

Analyse de la variance à deux facteurs

Également appelé two-way ANOVA (en), l'analyse de la variance à deux facteurs s'applique lorsque l'on souhaite prendre en compte deux facteurs de variabilité.

Décomposition de la variance

Soit un premier facteur de variabilité pouvant prendre les niveaux i = 1..p, un second facteur de variabilité pouvant prendre les niveaux j = 1..q, nij le nombre d'individu dans le niveau i du premier facteur et le niveau j du second facteur, n le nombre d'individu total et r le nombre d'individu dans chaque sous-groupe (pour un niveau i et un niveau j donné). La variable à expliquer s'écrit yijk avec i = 1..p, j = 1..ni et k = 1..mj.

La variable à expliquer peut être modélisée par la relation :

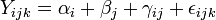
Y_{ijk} = \alpha_i + \beta_j + \gamma_{ij} + \epsilon_{ijk} ~

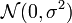
avec αi l'effet du niveau i du premier facteur, βj l'effet du niveau j du second facteur, γij l'effet d'interaction entre les deux facteurs et εijk l'erreur aléatoire (qui suit alors une loi normale \mathcal{N}(0, \sigma^2)~ ).

Le calcul présenté dans le cas à un facteur peut être transposé au cas à deux facteurs :

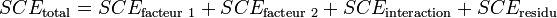
SCE_\text{total} = SCE_\text{facteur 1} + SCE_\text{facteur 2} + SCE_\text{interaction} + SCE_\text{residu}~

La part de la variance totale expliquée par le premier facteur (SCEfacteur 1), la part de la variance totale expliquée par le second facteur (SCEfacteur 2), l'interaction entre les deux facteurs (SCEinteraction) et la part de la variance totale qui ne peut être expliquée par le modèle (SCEresidu, appelé aussi variabilité aléatoire ou bruit) sont données par les formules :

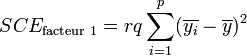
SCE_\text{facteur 1} = rq \sum_{i=1}^p (\overline{y_i} - \overline{y})^2
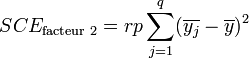
SCE_\text{facteur 2} = rp \sum_{j=1}^q (\overline{y_j} - \overline{y})^2
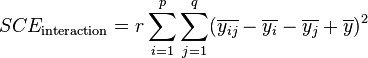
SCE_\text{interaction} = r \sum_{i=1}^p \sum_{j=1}^q (\overline{y_{ij}} - \overline{y_i} - \overline{y_j} + \overline{y})^2
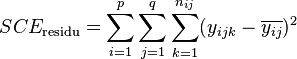
SCE_\text{residu} = \sum_{i=1}^p \sum_{j=1}^q \sum_{k=1}^{n_{ij}} (y_{ijk} - \overline{y_{ij}})^2

L'analyse de l'interaction entre facteurs est relativement complexe. Dans le cas où les facteurs sont indépendants, on peut s'intéresser qu'aux effet principaux des facteurs. La formule devient alors :

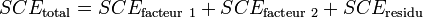
SCE_\text{total} = SCE_\text{facteur 1} + SCE_\text{facteur 2} + SCE_\text{residu} ~

Exemple illustratif

Notre exploitant laitier souhaite améliorer la puissance de son analyse en augmentant la taille de son étude. Pour cela, il inclut les données provenant d'une autre exploitation. Les chiffres qui lui sont fournit sont les suivant :

  • Pour la race A : 22,8 ; 21,7 ; 23,3 ; 23,1 ; 24,1 ; 22,3 et 22,7
  • Pour la race B : 23,1 ; 22,9 ; 21,9 ; 23,4 et 23,0
  • Pour la race C : 31,7 ; 33,1 ; 32,5 ; 35,1 ; 32,2 et 32,6

Analyse réalisée avec R :

      > produc ← c(20.1, 19.8, 21.3, 20.7, 22.6, 24.1, 23.8, 22.5, 23.4,       24.5, 22.9, 31.2, 31.6, 31.0, 32.1, 31.4, 22.8, 21.7, 23.3, 23.1,       24.1, 22.3, 22.7, 23.1, 22.9, 21.9, 23.4, 23.0, 31.7, 33.1, 32.5,       35.1, 32.2, 32.6)            > race ← as.factor(c("A", "A", "A", "A", "B", "B", "B", "B", "B",       "B", "B", "C", "C", "C", "C", "C", "A", "A", "A", "A", "A", "A",       "A", "B", "B", "B", "B", "B", "C", "C", "C", "C", "C", "C"))            > centre ← as.factor(c(rep("premier", 16), rep("second", 18)))            > anova(lm(produc~race*centre))      Analysis of variance Table            Response: produc                     Df    Sum Sq    Mean Sq     F value       Pr(>F)          race            2    696.48     348.24    559.6811    < 2.2e-16 ***      centre          1      8.46       8.46     13.6012    0.0009636 ***      race:centre     2     12.23       6.11      9.8267    0.0005847 ***      Residuals      28     17.42       0.62                             ---      Signif. codes:    0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Analyse de la variance à un facteur

Également appelé one-way ANOVA (en), l'analyse de la variance à un facteur s'applique lorsque l'on souhaite prendre en compte un seul facteur de variabilité.

Notation

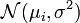
Considérons I échantillons Yi d'effectifs ni, issu des I populations qui suivent I lois normales \mathcal{N}(\mu_i, \sigma^2) de même variance. Chaque individu s'écrit yij, avec i \in [1, I] et j \in [1, n_i] . L'effectif total est .

Les moyennes par échantillon et totale s'écrivent :

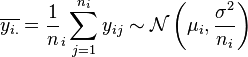
\overline{y_{i.}} = \frac 1 n_i \sum_{j=1}^{n_i} {y_{ij}} \sim \mathcal{N}\left( \mu_i, \frac {\sigma^2} {n_i} \right)
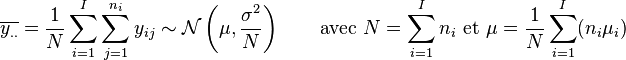
\overline{y_{..}} = \frac 1 N \sum_{i=1}^I \sum_{j=1}^{n_i} {y_{ij}} \sim \mathcal{N}\left( \mu, \frac {\sigma^2} N \right) \qquad \text{avec} ~ N = \sum_{i=1}^I n_i ~ \text{et} ~ \mu = \frac 1 N \sum_{i=1}^I (n_i \mu_i)

Décomposition de la variance

Le modèle s'écrit :

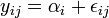
y_{ij} = \alpha_i + \epsilon_{ij} ~

Dans ces conditions, on montre que la somme des carrés des écarts (et donc la variance) peut être calculée simplement par la formule :

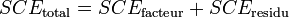
SCE_\text{total} = SCE_\text{facteur} + SCE_\text{residu} ~

La part de la variance totale SCEtotal qui peut être expliquée par le modèle (SCEfacteur, aussi appelée variabilité inter-classe, SSB ou Sum of Square Between class) et la part de la variance totale SCEtotal qui ne peut être expliquée par le modèle (SCEresidu aussi appelée variabilité aléatoire, variabilité intra-classe, bruit, SSW ou Sum of Square Within class) sont données par les formules :

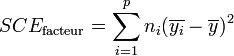
SCE_\text{facteur} = \sum_{i=1}^p n_i (\overline{y_i} - \overline{y})^2
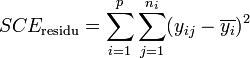
SCE_\text{residu} = \sum_{i=1}^p \sum_{j=1}^{n_i} (y_{ij}- \overline{y_i})^2
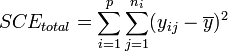
SCE_{total} = \sum_{i=1}^p \sum_{j=1}^{n_i} (y_{ij} - \overline{y})^2 .
 
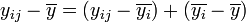
En décomposant ~ y_{ij} - \overline{y} = (y_{ij} - \overline{y_i}) + (\overline{y_i} - \overline{y}) ,
 
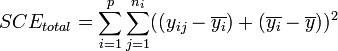
on peut écrire ~ SCE_{total} = \sum_{i=1}^p \sum_{j=1}^{n_i} ((y_{ij}- \overline{y_i}) + (\overline{y_i} - \overline{y}))^2
 
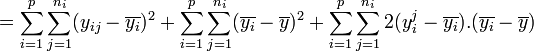
= \sum_{i=1}^p \sum_{j=1}^{n_i} (y_{ij}- \overline{y_i})^2 + \sum_{i=1}^p \sum_{j=1}^{n_i} (\overline{y_i} - \overline{y})^2 + \sum_{i=1}^p \sum_{j=1}^{n_i} 2( y_i^j - \overline{y_i}).(\overline{y_i} - \overline{y}) .
 
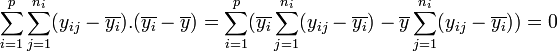
En remarquant que ~ \sum_{i=1}^p \sum_{j=1}^{n_i} ( y_{ij} - \overline{y_i}).(\overline{y_i} - \overline{y}) = \sum_{i=1}^p (\overline{y_i} \sum_{j=1}^{n_i} (y_{ij} - \overline{y_i}) - \overline{y} \sum_{j=1}^{n_i} (y_{ij} - \overline{y_i})) = 0 ,
 
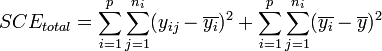
on peut écrire ~ SCE_{total} = \sum_{i=1}^p \sum_{j=1}^{n_i} (y_{ij} - \overline{y_i})^2 + \sum_{i=1}^p \sum_{j=1}^{n_i} (\overline{y_i} - \overline{y})^2
 
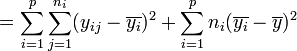
= \sum_{i=1}^p \sum_{j=1}^{n_i} (y_{ij} - \overline{y_i})^2 + \sum_{i=1}^p n_i (\overline{y_i} - \overline{y})^2
 
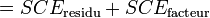
= SCE_\text{residu} + SCE_\text{facteur} ~ .

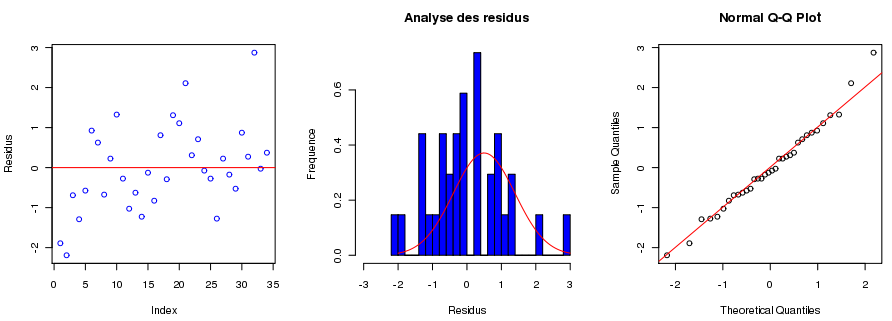
Analyse des résidus

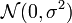
Il est toujours possible que le modèle ne soit pas correct et qu'il existe un facteur de variabilité inconnu (ou supposé a priori inutile) qui ne soit pas intégré dans le modèle. Il est possible d'analyser la normalité de la distribution des résidus pour rechercher ce type de biais. Les résidus, dans le modèle, doivent suivre une loi normale \mathcal{N}(0, \sigma^2)~ ). Tout écart significatif par rapport à cette loi normale peut être testé ou visualisé graphiquement :

Analyse residus.png
layout(matrix(1:3, 1, 3))
produc ← c(20.1, 19.8, 21.3, 20.7, 22.6, 24.1, 23.8, 22.5, 23.4, 24.5, 22.9, 31.2, 31.6, 31.0, 32.1, 31.4, 22.8, 21.7, 23.3, 23.1, 24.1, 22.3, 22.7, 23.1, 22.9, 21.9, 23.4, 23.0, 31.7, 33.1, 32.5, 35.1, 32.2, 32.6)
race ← as.factor(c("A", "A", "A", "A", "B", "B", "B", "B", "B", "B", "B", "C", "C", "C", "C", "C", "A", "A", "A", "A", "A", "A", "A", "B", "B", "B", "B", "B", "C", "C", "C", "C", "C", "C"))
plot(residuals(lm(produc~race)), ylab="Residus", col="blue")
abline(0, 0, col="red")
hist(residuals(lm(produc~race)), nclass=20, xlab="Residus", ylab="Frequence", xlim=c(-3,3), pro=T, col="blue", main="Analyse des residus")
lines(seq(-3,3,le=100), dnorm(seq(-3,3,le=100), 0, sqrt(var(residuals(lm(produc~race))))), col="red")
qqnorm(residuals(lm(produc~race)))
qqline(residuals(lm(produc~race)), col="red")
 

Test de Fisher

Degrés de liberté et variances

Par hypothèse, la variable observée yi suit une loi normale. La loi du χ² à k degrés de liberté étant définit comme étant la somme de k lois normales au carré, les sommes des carrés des écarts SCE suivent les lois du χ² suivantes, avec p le nombre de niveaux du facteur de variabilité et n le nombre total d'individu :

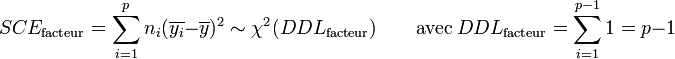
SCE_\text{facteur} = \sum_{i=1}^p n_i (\overline{y_i} - \overline{y})^2 \sim \chi^2(DDL_\text{facteur}) \qquad \text{avec} ~ DDL_\text{facteur} = \sum_{i=1}^{p-1} 1 = p-1
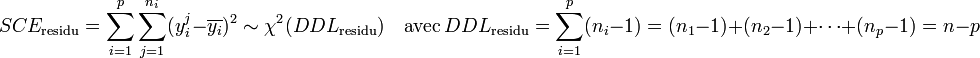
SCE_\text{residu} = \sum_{i=1}^p \sum_{j=1}^{n_i} (y_i^j - \overline{y_i})^2 \sim \chi^2(DDL_\text{residu}) \quad \text{avec} ~ DDL_\text{residu} = \sum_{i=1}^p (n_i - 1) = (n_1-1)+(n_2-1)+\cdots+(n_p-1) = n - p

Les variances s'obtiennent en faisant le rapport de la somme des carrés des écarts sur le nombre de degrés de liberté :

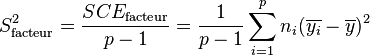
S^2_\text{facteur} = \frac {SCE_\text{facteur}} {p-1} = \frac 1 {p-1} \sum_{i=1}^p n_i (\overline{y_i} - \overline{y})^2
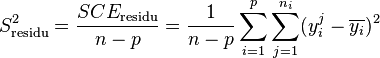
S^2_\text{residu} = \frac {SCE_\text{residu}} {n-p} = \frac 1 {n-p} \sum_{i=1}^p \sum_{j=1}^{n_i} (y_i^j - \overline{y_i})^2

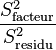
La Loi de Fisher étant défini comme le rapport de deux lois du χ², le rapport \frac {S^2_\text{facteur}} {S^2_\text{residu}} soit donc une Loi de Fisher :

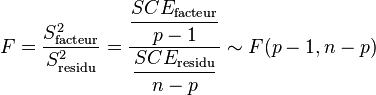
F = \frac {S^2_\text{facteur}} {S^2_\text{residu}} = \frac {\dfrac {SCE_\text{facteur}} {p-1}} {\dfrac {SCE_\text{residu}} {n-p}} \sim F(p-1, n-p)
Remarque

Pour les amateurs de géométrie vectorielle, la décomposition des degrés de liberté correspond à la décomposition d'un espace vectoriel de dimension nm en sous espaces supplémentaires et orthogonaux de dimensions respectives m − 1 et m(n − 1). Voir par exemple le cours dispensé par Toulouse III : [1] pages 8 et 9. On peut se reporter aussi au livre classique de Scheffé (1959)

Test d'adéquation à la loi de Fisher

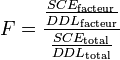
F = \frac {\frac {SCE_\text{facteur}} {DDL_\text{facteur}}} {\frac {SCE_\text{total}} {DDL_\text{total}}}

Il se trouve (comme on peut le voir dans la décomposition mathématique) que les deux termes sont tous les deux une estimation de la variabilité résiduelle si le facteur A n'a pas d'effet. De plus, ces deux termes suivent chacun une loi de χ², leur rapport suit donc une loi de F (voir plus loin pour les degrés de liberté de ces lois). Résumons :

  • Si le facteur A n'a pas d'effet, le rapport de Sa et Sr suit une loi de F et il est possible de vérifier si la valeur du rapport est « étonnante » pour une loi de F
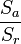
  • Si le facteur A a un effet, le terme Sa n'est plus une estimation de la variabilité résiduelle et le rapport \frac{S_{a}}{S_{r}} ne suit plus une loi de F. On peut comparer la valeur du rapport à la valeur attendue pour une loi de F et voir, là aussi, à quel point le résultat est « étonnant ».

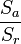
Résumer les choses ainsi permet de clarifier l'idée mais renverse la démarche : on obtient en pratique une valeur du rapport \frac{S_{a}}{S_{r}} qu'on compare à une loi de F, en se donnant un risque α (voir l'article sur les tests et leurs risques). Si la valeur obtenue est trop grande, on en déduit que le rapport ne suit vraisemblablement pas une loi de F et que le facteur A a un effet. On conclut donc à une différence des moyennes.

CMB est l'estimateur SA présenté au paragraphe précédent (première approche technique) et CMW l'estimateur SB. On en déduit le F de Fisher, dont la distribution est connue et tabulée sous les hypothèses suivantes :

  • Les résidus ε sont distribués normalement
  • Avec une espérance nulle
  • Avec une variance σ2 indépendante de la catégorie i
  • Avec une covariance nulle deux à deux (indépendance)

Le respect de ces hypothèses assure la validité du test d'analyse de la variance. On les vérifie a posteriori par diverses méthodes (tests de normalité, examen visuel de l'histogramme des résidus, examen du graphique des résidus en fonction des estimées) voir condition d'utilisation ci-dessous.

Table d'ANOVA

La table d'ANOVA permet de résumer les calculs nécessaires :

Source de la variance Sommes des
carrés des écarts		 Degrés de liberté Variance F p-value
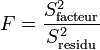
Inter-classes SCEfacteur DDLfacteur S^2_\text{facteur} = \frac {SCE_\text{facteur}} {DDL_\text{facteur}} F = \frac {S^2_\text{facteur}} {S^2_\text{residu}} P_{H_0}(F>F_{obs})
Intra-classe SCEresidu DDLresidu S^2_\text{residu} = \frac {SCE_\text{residu}} {DDL_\text{residu}}
Total SCEtotal DDLtotal

Exemple illustratif

Prenons un exemple pour illustrer la méthode. Imaginons un éleveur qui souhaite acheter de nouvelles vaches pour sa production laitière. Il possède trois races différentes de vaches et se pose donc la question de savoir si la race est importante pour son choix. Il possède comme informations la race de chacune de ses bêtes (c'est la variable explicative discrète ou facteur de variabilité, qui peut prendre 3 valeurs différentes) et leurs productions de lait journalières (c'est la variable à expliquer continue, qui correspond au volume de lait en litre).

Dans notre exemple, l'hypothèse nulle revient à considérer que toutes les vaches produisent la même quantité de lait journalière (au facteur aléatoire près) quelle que soit la race. L'hypothèse alternative revient à considérer qu'une des races produit significativement plus ou moins de lait que les autres.

Supposons que les productions sont :

  • Pour la race A : 20,1 ; 19,8 ; 21,3 et 20,7
  • Pour la race B : 22,6 ; 24,1 ; 23,8 ; 22,5 ; 23,4 ; 24,5 et 22,9
  • Pour la race C : 31,2 ; 31,6 ; 31,0 ; 32,1 et 31,4
Race Taille Moyenne Variance
A 4 20,475 0,4425
B 7 23,4 0,59333
C 5 31,46 0,178
Total 16 25,1875 20,90117
Table d'ANOVA
Source de la variance Sommes des
carrés des écarts		 Degrés de liberté Variance F p-value
Inter-classes 307,918 2 153,959 357,44 4,338e-12
Intra-classe 5,6 13 0,431
Total 313.518 15
Analyse réalisée avec R 
      > produc ← c(20.1, 19.8, 21.3, 20.7, 22.6, 24.1, 23.8, 22.5,       23.4, 24.5, 22.9, 31.2, 31.6, 31.0, 32.1, 31.4)      > race ← as.factor(c("A", "A", "A", "A", "B", "B", "B", "B", "B",       "B", "B", "C", "C", "C", "C", "C"))            # Regardons les moyennes par groupe:      > tapply(produc, race, mean)      A         B         C       20.475    23.400    31.460      # On remarque des différences entre groupes, mais sont-elles statistiquement significatives?            # Testons le par l'ANOVA:      > anova(lm(produc~race))      Analysis of variance Table            Response: produc                   Df     Sum Sq    Mean Sq    F value       Pr(>F)      race          2    307.918    153.959     357.44    4.338e-12 ***      Residuals    13      5.600      0.431             Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Les résultats de l'analyse sont présentés dans un tableau (les couleurs ont été ajoutées pour faciliter l'explication). Le tableau contient 3 lignes : la première contient les titres des colonnes, la dernière contient l'analyse des résidus. Le tableau contient également une ligne par facteur de variabilité (une seule dans cet exemple).

  • La première colonne (en rouge) indique les facteurs analysés : le facteur "race" et les résidus ("Residuals" (en)).
  • La seconde colonne (en bleu) indique le nombre de degrés de liberté : 3 races différentes - 1 = 2 degrés de libertés pour le facteur "race" ; 16 individus dans l'étude - 3 niveaux pour le facteur "race" = 13 degrés de liberté pour les résidus.
  • La cinquième colonne (en vert) indique le F calculé dans cet exemple.
  • La sixième colonne (en marron) indique la probabilité que l'hypothèse nulle soit vraie (p-value). Dans cet exemple, la valeur très basse indique que l'on peut rejeter l'hypothèse nulle avec très peu de risque : l'agriculteur peut conclure "les 3 races de vaches ne produisent pas la même quantité journalière de lait". Le nombre d'étoiles à côté de la valeur de p indique la confiance que l'on peut accorder au résultat : 3 étoiles indiquent que le résultat est très sûr (p-value < 0,001).
Principe
Limites d'utilisation de l'analyse de la variance
- Introduction - Principe - Analyse de la variance à deux facteurs - Analyse de la variance à un facteur - Limites d'utilisation de l'analyse de la variance - Analyse de la variance multifactorielle
miniature
Une éruption volcanique en 2018 responsable d'une explosion de vie 🌋
miniature
Un système d'exploitation pour les ordinateurs quantiques voit le jour 🖥️
miniature
Des singularités temporelles dans l'Univers ? 🕰️
miniature
Des fossiles de dinosaures mieux datés 🦖
miniature
Une gigantesque muraille de 10 milliards d'années-lumière dans l'Univers 🔭
miniature
Benchmark: les processeurs quantiques sous la loupe, quels sont les meilleurs ? 🏆
miniature
Découverte d'une "fourmi de l'enfer" vieille de 113 millions d'années 🐜
miniature
Le rôle méconnu de la décharge dans l'usure des batteries 🔋
miniature
1
La fonte des glaces déplace les pôles: quelles conséquences ? 🌍
miniature
L'appareil photo de votre smartphone peut détecter l'antimatière 📱
miniature
Cette étoile-zombie peut déformer les atomes à distance, et elle fonce dans notre galaxie ⭐
miniature
Un mosasaure géant découvert dans le Mississippi 🦕
miniature
Problème, les galaxies meurent plus tôt que prévu 🌀
miniature
Ce lien entre cannabis et troubles psychotiques 🧠
miniature
Une révolution dans le refroidissement des puces électroniques ? 🔥
miniature
Des parasites sous-marins filmés en train de vampiriser un poisson des abysses 👀
miniature
Lucy survole un astéroïde en forme de cacahuète 🚀
miniature
Découverte du fossile d'un dinosaure géant méconnu 🦕
miniature
Mars avait-elle un champ magnétique unilatéral ? 🔍
miniature
Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇
miniature
Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁
miniature
L'électroluminescence du graphène, une découverte inattendue ! 💡
miniature
Cet objet métallique n'a pas été fabriqué sur Terre 🔧
miniature
1
Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡
miniature
Cette super-Terre brûle les attentes des astronomes 🔥
miniature
Découverte exceptionnelle de fossiles d'amphibiens géants 🐸
miniature
Voici ce qui a causé les toutes premières inégalités de richesse 💰
miniature
Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊
miniature
Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭
miniature
Des cellules solaires flexibles battent des records d'efficacité ⚡
miniature
Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀
miniature
Record établi pour un transistor en diamant 💎
miniature
Les sursauts radio rapides trahissent enfin leur origine cosmique 📡
miniature
Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠
miniature
Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊
miniature
Les oscillations collectives des foules humaines denses 🔁
miniature
Une forme inconnue de la matière détectée au LHC ? ⚛️
miniature
Le sel, un facteur méconnu de l'obésité ? 🧂
miniature
L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀
miniature
Découverte tectonique majeure sous les Petites Antilles 🌍
miniature
1
Peut-on geler en chauffant ? ❄️
miniature
Une peau électronique pour doter les robots du sens du toucher 👌
miniature
Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳
miniature
Le cancer inscrit dans nos gènes dès la naissance ? 🧬
miniature
Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥
miniature
Le passé verdoyant du plus grand désert du monde 🐪
miniature
Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷
miniature
Des puces quantiques plus proches que jamais ⚡
miniature
1
Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬
miniature
En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊
Page générée en 0.135 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise