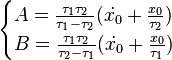Amortissement physique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
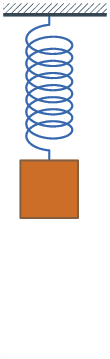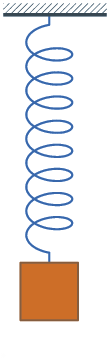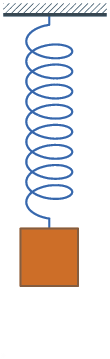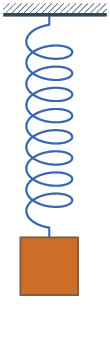
En physique, l'amortissement est l'effet engendré par l'entrée d'un système, qui tend à s'opposer aux variations de la sortie du système.
Explication
Dans tout système réel, une partie de l'énergie totale est dissipée, le plus souvent en chaleur, ce qui crée une force d'amortissement.
En mécanique, celle-ci dépend de la vitesse du corps. Dans de nombreux cas, on peut supposer que le système est linéaire, l'amortissement étant alors proportionnel à la vitesse (voir Système oscillant à un degré de liberté).
En électricité, l'amortissement désigne l'effet résistif d'un circuit RLC.
On définit le coefficient d'amortissement c par :
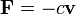
Lexique
- Facteur d'amortissement ou facteur de perte (loss factor), η, d'une matière viscoélastique (nombre sans dimension). Il dépend de la température et de la fréquence de la vibration excitatrice. Il peut être mesuré par analyse mécanique dynamique (AMD ou DM(T)A).
- Coefficient d'amortissement : expression en kilogrammes par seconde. On observe qu'il existe un ensemble de forces extérieures au corps, qui sont proportionnelles à la vitesse du corps. On désigne par coefficient d'amortissement le rapport entre ces forces-là et la vitesse.
- Constante de raideur : expression en newtons par mètre. On observe qu'il existe un ensemble de forces extérieures au corps, qui sont proportionnelles au déplacement du corps. On désigne par constante de raideur le rapport entre ces forces-là et le déplacement.
- Constante de temps : expression en seconde. Généralement, on note la puissance d'une exponentielle négative faisant uniquement intervenir le temps comme le rapport entre celui-ci et un coefficient, homogène lui aussi à un temps, qui prend le nom de constante de temps. Elle traduit une échelle le temps pour l'équilibre du phénomène modélisé.
- Pseudo-pulsation propre : expression en radians par seconde. Il s'agit de la pulsation du régime pseudo-périodique, liée à la fréquence du phénomène amortie.
Exemple : Masse-Ressort-Amortisseur
Étudions un système idéal Masse-Ressort-Amortisseur, avec une masse m fixée (dans le sens où le corps garde la même masse tout au long de l'étude), une constante de raideur k, et un coefficient d'amortissement c :
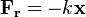
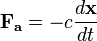
La masse est un corps libre. On suppose le repère inertiel, donc le premier vecteur est parallèle au ressort et à l'amortisseur. D'après la conservation de la quantité de mouvement :
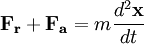
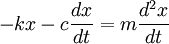
Équation différentielle ordinaire
C'est une équation différentielle ordinaire du second ordre. Elle est linéaire, homogène et à coefficients constants :
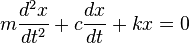
Afin de simplifier l'équation, nous définissons deux paramètres :
- la pulsation naturelle du système :
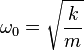
- et le taux d'amortissement :
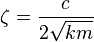
Ainsi, l'équation différentielle devient :
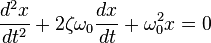
On résout le polynôme caractéristique :
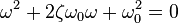
d'où
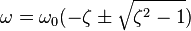
Régime transitoire du système
Le comportement du système dépend de la pulsation naturelle, et du taux d'amortissement. En particulier, il dépend fortement de la nature de ω.
Régime pseudo-périodique
ζ < 1, les racines ω sont complexes et conjuguées. La solution est la somme de deux exponentielles complexes :
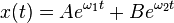
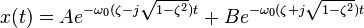
On peut réécrire la solution sous une forme trigonométrique :
![x(t) = e^{ - \frac{t}{\tau}}[A \cos(\omega_d t) + B \sin(\omega_d t)]](https://static.techno-science.net/illustration/Definitions/autres/9/99741432c6008f0c8afe9cf67836197b_e6d5a9ecf3c5effd7b30ad6133be8666.png)
où
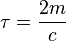
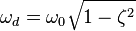
On détermine la plupart du temps les constantes A et B grâce aux conditions initiales x0 et
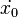
![\frac{dx}{dt} = e^{ - \frac{t}{\tau}}( [\omega_d B - \frac{A}{\tau}] \cos(\omega_d t) - [\omega_d A + \frac{B}{\tau}] \sin(\omega_d t))](https://static.techno-science.net/illustration/Definitions/autres/c/ceb27b9da7576586c0db3932b6c7267f_8efff52ec3d7c59dccf263aa29ffd3ab.png)
On résout le système d'équations linéaires :
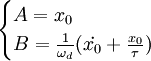
On obtient la solution homogène générale :
![x(t) = e^{ - \frac{t}{\tau}}[x_0 \cos(\omega_d t) + \beta \sin(\omega_d t)]](https://static.techno-science.net/illustration/Definitions/autres/d/d9713e6e38ca02b907d2f0b2e5f2803f_e98ea6a143ded24039685b0a6cbe581d.png)
Régime apériodique critique
ζ = 1, la racine ω est réelle et double. La solution est le produit d'un polynôme d'ordre 1 et d'une exponentielle réelle :
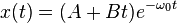
Comme ω0 est réelle, elle traduit non plus une pulsation mais une constante de temps, donc on note
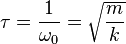
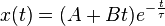
On détermine la plupart du temps les constantes A et B grâce aux conditions initiales x0 et
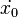
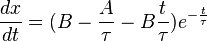
On résout le système d'équations linéaires :
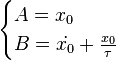
On obtient la solution homogène générale :
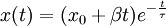
Régime apériodique
ζ > 1, les racines ω sont réelles et distinctes. La solution est la somme de deux exponentielles réelles :
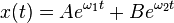
Comme ω1 et ω2 sont réelles, elle traduisent non plus une pulsation mais une constante de temps, donc on note
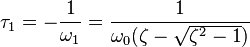
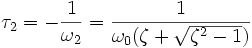
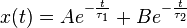
On détermine la plupart du temps les constantes A et B grâce aux conditions initiales x0 et
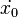
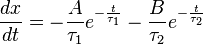
On résout le système d'équations linéaires :