Algèbre universelle - Définition

Quotients et congruences

Définition et propriétés élémentaires

Il est courant de définir le groupe quotient d'un groupe par un sous-groupe distingué, l'anneau quotient d'un anneau par un idéal bilatère ou le module quotient d'un module par un sous-module. Mais la généralisation de ces notions dans le cadre de l'algèbre universelle est moins immédiate. Ces quotients sont en fait des quotients par rapport à des relations d'équivalence particulières et dans ces exemples, les classes d'équivalence d'élément neutre (e, 1 et 0 respectivement) sont les sous-groupes distingués, les idéaux bilatères et les sous-modules.

Soit A une algèbre de signature Ω. On appelle congruence (ou Ω-congruence si on tient à préciser) de A toute relation d'équivalence R dans A telle que, pour tout entier naturel n, pour tout élément ω de Ω_n quels que soient les éléments x₁, ..., x_n, y₁, ..., y_n de A, si, pour i = 1, ..., n, x_i et y_i sont équivalents pour R, alors ω_A(x₁, ..., x_n) = ω_A(y₁, ..., y_n) sont équivalents pour R.

Soit R une congruence de A. Alors chacune des opérations de A passe au quotient suivant R, c'est-à-dire produit une opération « bien définie » dans l'ensemble quotient A/R : le composé des classe d'équivalence d'éléments de A pour R est la classe d'équivalence du composé de ces éléments de A pour R. On définit ainsi une structure algébrique sur A/R, et l'algèbre ainsi obtenue est appelée algèbre quotient ou, plus simplement, quotient de A par R. Lorsque l'on considère l'ensemble A/R comme une algèbre de signature Ω, c'est pour cette structure algébrique.

La surjection canonique de A sur A/R est un homomorphisme. En fait, la structure algébrique de A/R est l'unique structure algébrique sur l'ensemble A/R pour laquelle cette surjection est un homomorphisme.

Revenons sur le cas des groupes. Soit G un groupe. Alors, pour tout sous-groupe distingué H de G, la relation d'équivalence dans G définie par H (x et y sont équivalents si et seulement si xy ^{− 1} appartient à H) est une congruence de G. Réciproquement, pour toute congruence R de G, la classe d'équivalence de l'élément neutre de G est un sous-groupe distingué de G. On obtient ainsi une bijection entre les congruences de G et les sous-groupes distingués de G. On obtient des résultats analogues pour les anneaux et les modules en remplaçant les sous-groupes distingués par les idéaux bilatères et les sous-modules, respectivement.

Les congruences de A ne sont autres que les sous-algèbres de l'algèbre produit A × A.

Voici quelques propriétés des congruences.

• L'identité de l'ensemble A et l'ensemble A × A sont des congruences de A.
• L'intersection d'un ensemble de congruences de A est une congruence de A.
• Soit B une sous-algèbre de A. Pour toute congruence R de A, la relation d'équivalence dans B induite par R (son intersection R ∩ (B × B) avec B × B) est une congruence dans B, qui est dite induite sur B par R.
• Pour toute relation binaire R dans A, il existe une plus petite congruence de A qui la contienne, et c'est l'intersection de l'ensemble des congruences de A qui la contiennent, et elle est dite engendrée par R.
• L'ensemble des congruences de A est un treillis complet pour la relation d'inclusion, c'est-à-dire toute ensemble de congruences de A admet, pour la relation d'inclusion, une borne inférieure et une borne supérieure. Dans ce treillis, la borne inférieure d'une famille de congruences est son intersection et la borne supérieur est la congruence engendrée par sa réunion.

Exemple de géométrie affine. Soient K un corps et E un espace affine sur K attaché à un espace vectoriel V sur K. On considère E comme un algèbre pour une signature convenable (voir plus haut). Pour tout sous-espace vectoriel W de V, l'ensemble des couple (x, y) de points de E tels que x - y appartient à V est une congruence de cette algèbre, et on obtient ainsi une bijection entre le treillis des congruences de E est celui des sous-espaces vectoriels de V.

Passage au quotient et théorèmes d'isomorphie

Comme dans le cas des groupes, des anneaux et des modules, il y a une notion de passage au quotient d'homomorphismes et il y a des théorèmes d'isomorphie.

Premier théorème d'isomorphie. Soient A et B des algèbres, f un homomorphisme de A dans B. Alors la relation d'équivalence U dans A associée à f (x est équivalent à y pour U si et seulement si f(x) = f(y)) est une congruence dans A, dite associée à f et est notée R_f, et l'application g de A/R_f dans B déduite de f par passage au quotient est un homomorphisme injectif, et un donc g définit un isomorphisme de A/R_f sur f(B). Si f est une surjection, alors g est un isomorphisme de A/R_f sur B.

Plus généralement, si R et S sont des congruences de A et B respectivement et si, quels que soient les éléments x et y de A qui sont équivalents pour R, f(x) et f(y) sont équivalents pour S (on dit alors que f est compatible avec R et S), alors, par passage au quotient, on définit une application de A/R dans B/S, et cette application est un homomorphisme.

Proposition. Soit R une relation d'équivalence dans une algèbre A. Pour que R soit une congruence de A, il faut et il suffit qu'il existe un homomorphisme f de A dans une algèbre B tel que R est la congruence de A associée à f.

Définition. On dit qu'une algèbre B est image homomorphe d'une algèbre A s'il existe un homomorphisme surjectif f de A sur B, et alors B est isomorphe à l'algèbre A/R, où R est la congruence de A associée à f.

Voici la propriété fondamentale des algèbres quotients.

Théorème. Soient A et B des algèbres, R une congruence de A et p la surjection canonique de A sur A/R. Pour tout homomorphisme f de A/R dans B, alors f p est un homomorphisme de A dans B qui est compatible avec R. L'application f f p de l'ensemble des homomorphismes de A/R dans B dans l'ensemble des homomorphismes de A dans B qui sont compatibles avec R est une bijection. En termes de théorie des catégories, cela peut s'interpréter en disant que le couple (A/B, p) est du foncteur de la catégorie des algèbres de signature Ω dans la catégorie des ensembles qui à toute algèbre X de signature Ω associe l'ensemble des homomorphismes de A dans X qui sont compatibles avec R est représentant.

Définition. Soient A une algèbre, B une sous-algèbre de A et R une congruence de A. On dit que B est saturée pour R si la classe d'équivalence pour R de tout élément de B est incluse dans B, c'est-à-dire si B est la réunion de classes d'équivalence de R. La réunion de l'ensemble des classes d'équivalence pour R des éléments de B est une sous-algèbre de A qui est saturée pour R, et on l'appelle saturée de B pour R. Elle est égale à l'image R(B) de B par la relation R.

Proposition. Soient A et B des algèbres telles qu'il existe un homomorphisme f de A sur B et soit R la congruence de A associée à f. Alors l'application de l'ensemble des sous-algèbres de A qui sont saturée pour R dans l'ensemble des sous-algèbres de f(B) qui à une telle sous-algèbre C de A associe f(C) est une bijection.

Deuxième théorème d'isomorphie. Soient A une algèbre, B une sous-algèbre de A, R une congruence de A et C la saturé de B pour R. Alors l'injection canonique de B dans C est compatible avec les relations d'équivalence S et T induites sur B et C par R, et donc, on a par passage au quotient, un homomorphisme g de B/S dans C/T. Si de plus A = C, alors g est un isomorphisme de B/S sur A/R = C/T.

Troisième théorème d'isomorphie. Soient A une algèbre, R et S des congruences de A telles que R est incluse dans S. Alors l'identité de A est compatible avec R et S et alors la relation d'équivalence associée à l'application h de A/R sur A/S déduite de l'identité de A par passage au quotient est notée S/R et appelée quotient de S par R. L'application de (A/R)/(S/R) dans A/S déduite de h par passage au quotient est un isomorphisme (les R se simplifient).

Proposition. Soient A une algèbre et R une congruence de A. Alors l'application de l'ensemble des congruences de A qui contiennent R dans l'ensemble des congruences de A/R qui à toute congruence S de A qui contient R associe S/R est une bijection.

Proposition. Soit une famille d'algèbre et, pour tout élément i de I, R_i une congruence dans R_i. Alors la relation binaire R dans définie par R si et seulement si x_i R y_i est une congruence dans . Elle est la relation d'équivalence associée à l'homomorphisme g de dans qui à associe la famille des classes d'équivalence des x_i suivant des R_i. D'après le premier théorème d'isomorphie, on déduit de g par passage au quotient suivant R un isomorphisme de sur .

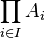
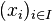
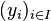
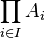
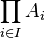
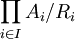
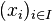
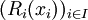
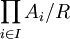
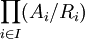
Algèbres simples

Définition. On dit qu'un algèbres A est simple si l'ensemble de ses congruences est un ensemble à deux éléments, c'est-à-dire si A n'est ni vide ni triviale et s'il n'existe pas de congruence autre que l'identité de A et la congruence A × A.

Cette définition généralise la notion de groupes simples, de modules simples sur un anneau donné. La définition des anneaux simples et des algèbres associatives unitaires simples sur un corps commutatif donné variant d'un auteur à l'autre, cette définition la généralise parfois. Dans le cas des algèbres de Lie sur un corps commutatif donné, on exige en plus que les algèbres de Lie simples soient non commutatives et de dimension finie.