Algèbre géométrique - Définition

Irrationnalité

Les grecs finirent par s'apercevoir que leur postulat initial était faux. Toutes les longueurs ne s'expriment pas comme une fraction de deux nombres entiers. Une question, naturelle pour un pythagoricien, est la détermination de la fraction de nombres entiers décrivant la proportion entre une diagonale et son côté, pour un pentagone ou un carré. Ce rapport n'est pas une fraction de nombre entier. Les méthodes de l'algèbre géométrique sont adaptés pour appréhender cette question. En termes modernes, la question est algébrique car elle correspond à la nature d'une solution d'une équation du second degré.

Les Pythagoriciens développaient le culte du secret, à propos de leurs savoirs, il est en conséquence difficile de connaître précisément quand, qui et avec quelles méthodes la découverte puis la démonstration ont été faite. Plusieurs hypothèses sont imaginées et, à ce jour, aucune ne fait l'unanimité.

Une découverte à l'aide du pentagone ?

Une méthode babylonienne met en évidence le caractère irrationnel de φ.

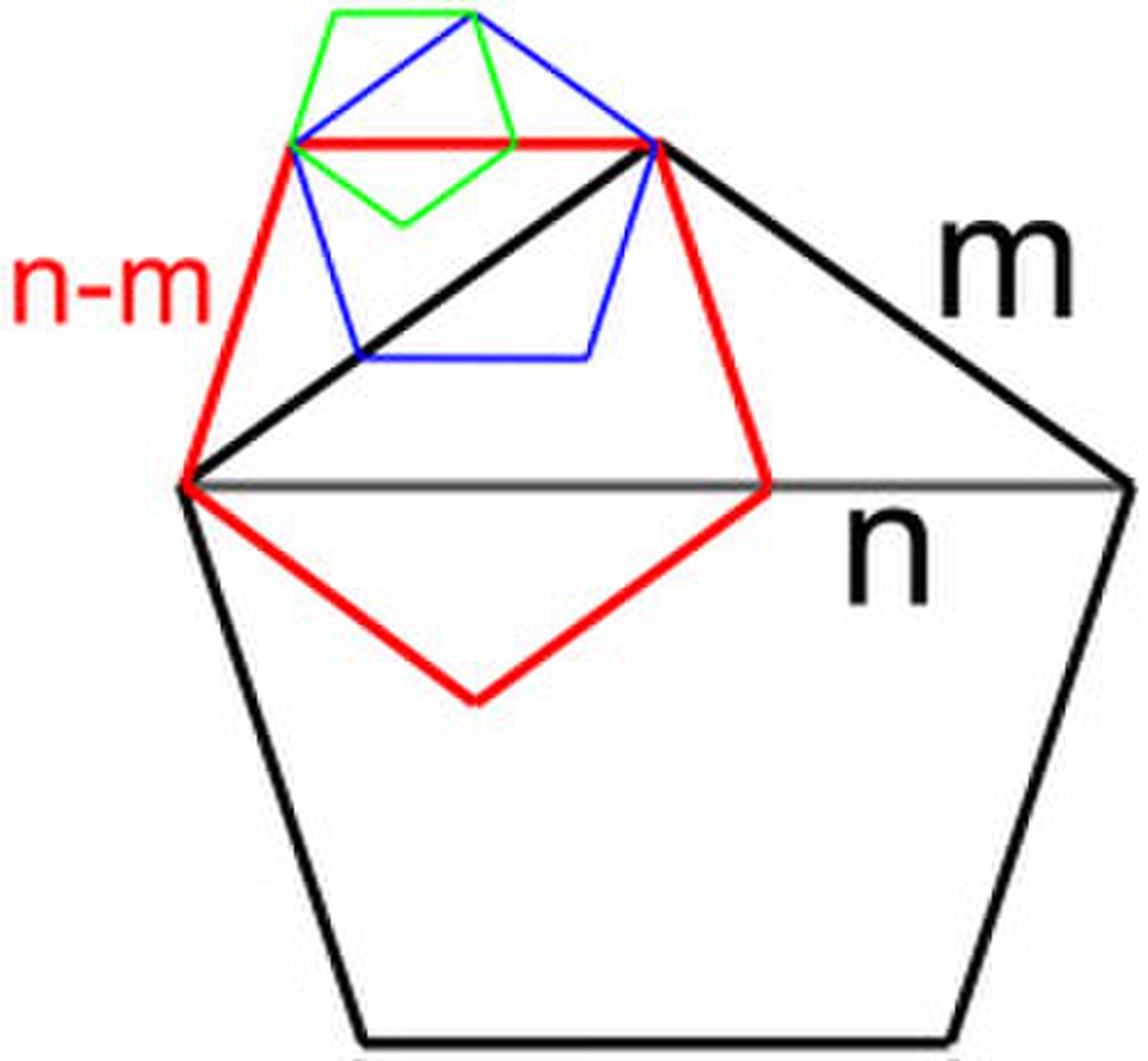
L'historien Kurt Von Fritz émet l'hypothèse suivante : Hippase, après avoir trouvé comment construire le pentagone, aurait cherché à déterminer la section d'extrême et de moyenne raison, c'est à dire le rapport entre une diagonale et un côté d'un pentagone régulier. Il imagine que cette section est une fraction n/m de deux nombres entiers. Une procédure pour trouver ces valeurs n et m consiste à construire un rectangle de base n et de hauteur m. On cherche à emplir ce rectangle de carrés de côté le plus grand possible. La première valeur du côté est m et on peut placer un unique carré, en rouge sur la figure.

Après avoir placé le carré rouge, la zone restante est un carré de côté m et n - m. En multipliant par n/m, on remarque que le carré est homothétique à un carré de hauteur m et de base n. Ce résultat est une conséquence de l'égalité 1/(φ - 1) = φ. On en déduit que l'on peut ensuite placer un unique carré, en bleu foncé sur la figure et de côté n - m. On en déduit surtout que la procédure ne s'arrête jamais !

Cette procédure, connue depuis les babyloniens sur le calcul du rapport entre la diagonale et le côté d'un carré, permet de donner une suite de fractions qui approxime de mieux en mieux la fraction φ. On obtient : 1, puis 2, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21 ..., c'est-à-dire des fractions de plus en plus proches de φ, avec des numérateurs et des dénominateurs qui ne cessent de croître. Ce comportement n'a aucun sens, les dénominateurs ne devraient jamais dépasser m. Les carrés rouge puis bleus ont nécessairement des côtés entiers. L'historien Maurice Caveing en conclut qu'il est raisonnable de penser que ces observations ont permis la réalisation d'une révélation stupéfiante : le fait que toutes les grandeurs ne sont pas des fractions^,.

Des fins possibles de la démonstration

Une descente infinie montre que φ est irrationnel.

Il existe d'autres manières de conclure à partir de la construction précédente. On suppose toujours que φ est un nombre rationnel, noté n/m, et on construit un pentagone régulier de coté m et de diagonale n. La figure de droite montre comment construire un nouveau pentagone, de côté n - m et de diagonale m, le côté et la diagonale du nouveau pentagone sont toujours des entiers, mais cette fois-ci plus petits. L'on peut ainsi continuer indéfiniment. La suite des côtés forment alors une liste d'entiers positifs strictement décroissante et infinie, ce qui est impossible. Un tel raisonnement s'appelle en mathématique une descente infinie.

Il existe aussi une manière plus rapide et plutôt plus simple de conclure. Avec les mêmes hypothèses, on choisit, pour valeur de n/m, une représentation irréductible, c'est à dire que m est la plus petite valeur que doit prendre le côté du pentagone pour que le diamètre soit de longueur entière. Le pentagone en rouge de la figure de droite montre qu'il est possible de construire un pentagone de côté n - m et de diagonale entière. Cette contradiction permet de conclure.

Il existe un consensus relativement vaste chez les historiens pour admettre qu'Hippase n'a pas pu terminer la démonstration. Par exemple, pour la descente infinie, Caveing remarque que : « Ce qui manque à la démonstration c'est seulement l'axiome d'Archimède, ou un lemme équivalent, qu'au témoignage d'Archimède lui-même on n'a pas le droit de faire remonter plus haut qu'Eudoxe de Cnide ». Ainsi, l'historien Maurice Caveing pense qu'à la période d'Hippase, aucune découverte scientifique fructueuse n'était possible.

Racine carrée de deux

Le double d'un nombre carré n'est jamais un nombre carré.

Le résultat précédent permet de déduire que la diagonale d'un carré de coté 1 est irrationnelle.

La logique présentée pour le pentagone s'applique aussi pour la diagonale du carré. On en retrouve des traces dans les livres d'Euclide. La preuve par la descente infinie se trouve dans le livre X, à la proposition 117. La démonstration que la fraction continue d'un nombre rationnel est finie se trouve dans le livre VII. Pour ce cas particulier, cet algorithme porte maintenant le nom d'algorithme d'Euclide. Il existe aussi une démonstration différente, encore présente chez Euclide, et citée par Aristote «  Ils prouvent que le diamètre du carré est incommensurable au côté en montrant que, si l'on admet qu'il lui est commensurable, un nombre impair serait égal à un pair. » L'historien O. Becker, montre que ce raisonnement est fondé sur un savoir archaïque des grecs en matière d'arithmétique géométrique, elle est peut-être très ancienne. La méthode consiste à démontrer que « Le double d'un nombre carré n'est jamais un nombre carré ». L'article racine carrée de deux montre comment elle est démontrée chez Euclide à l'aide d'un principe appelé lemme d'Euclide et plus tardif.

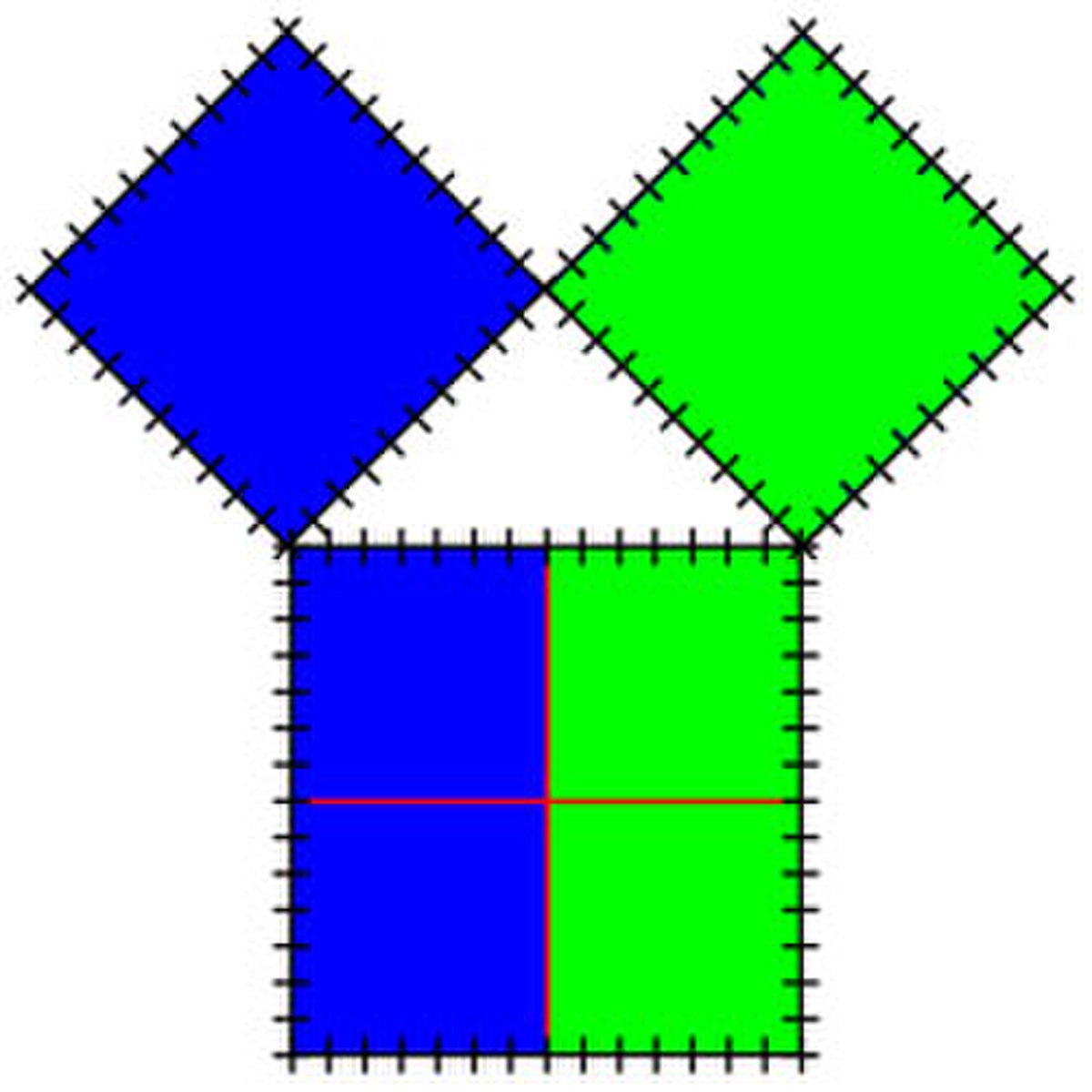
Une reconstitution de la possible démonstration archaïque, à base arithmétique géométrique, s'appuie sur la figure de gauche. Elle procède encore par l'absurde. On considère le plus petit nombre carré de côté a somme de deux nombres carrés de côté b. Le nombre carré de côté a est pair et donc a l'est aussi. Le côté b est impair, sinon, en choisissant une unité deux fois plus grande on trouverait une nouvelle valeur deux fois plus petite que a, dont le carré est la somme de deux carrés. Par ailleurs, un carré de côté b possède la même aire qu'un rectangle de hauteur a et deux fois plus grande que sa base (en bleu sur la figure). Un tel rectangle est composé de deux nombres carrés, il est donc pair et le carré de côté b l'est aussi, ainsi que b. Le côté b est un nombre à la fois pair et impair. Cette contradiction montre que b n'existe pas et termine la démonstration.

Une fois cette proposition démontrée, l'irrationnalité de la racine carrée de deux s'obtient en appliquant le théorème de Pythagore à la figure de droite. S'il existait une unité telle que tous les côtés du triangle rectangle isocèle de la figure soient des nombres entiers, le résultat précédent serait faux.

Conséquence

Le théorème de Thalès permet de généraliser la démonstration précédente.

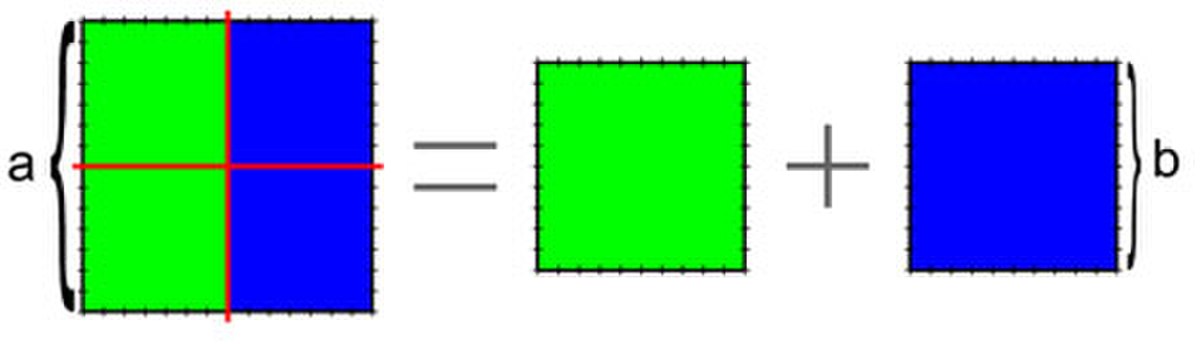
Une conséquence de l'existence d'irrationnels est que les démonstrations des propriétés établies sur les fractions d'entiers en début d'article ne traitent pas le cas général. Cependant, l'usage de l'algèbre géométrique et une approche différente permet encore de démontrer qu'une fraction b/c est égale à (a.b)/(a.c) si a, b, c sont trois nombres réels positifs tels que a et c soient non nuls.

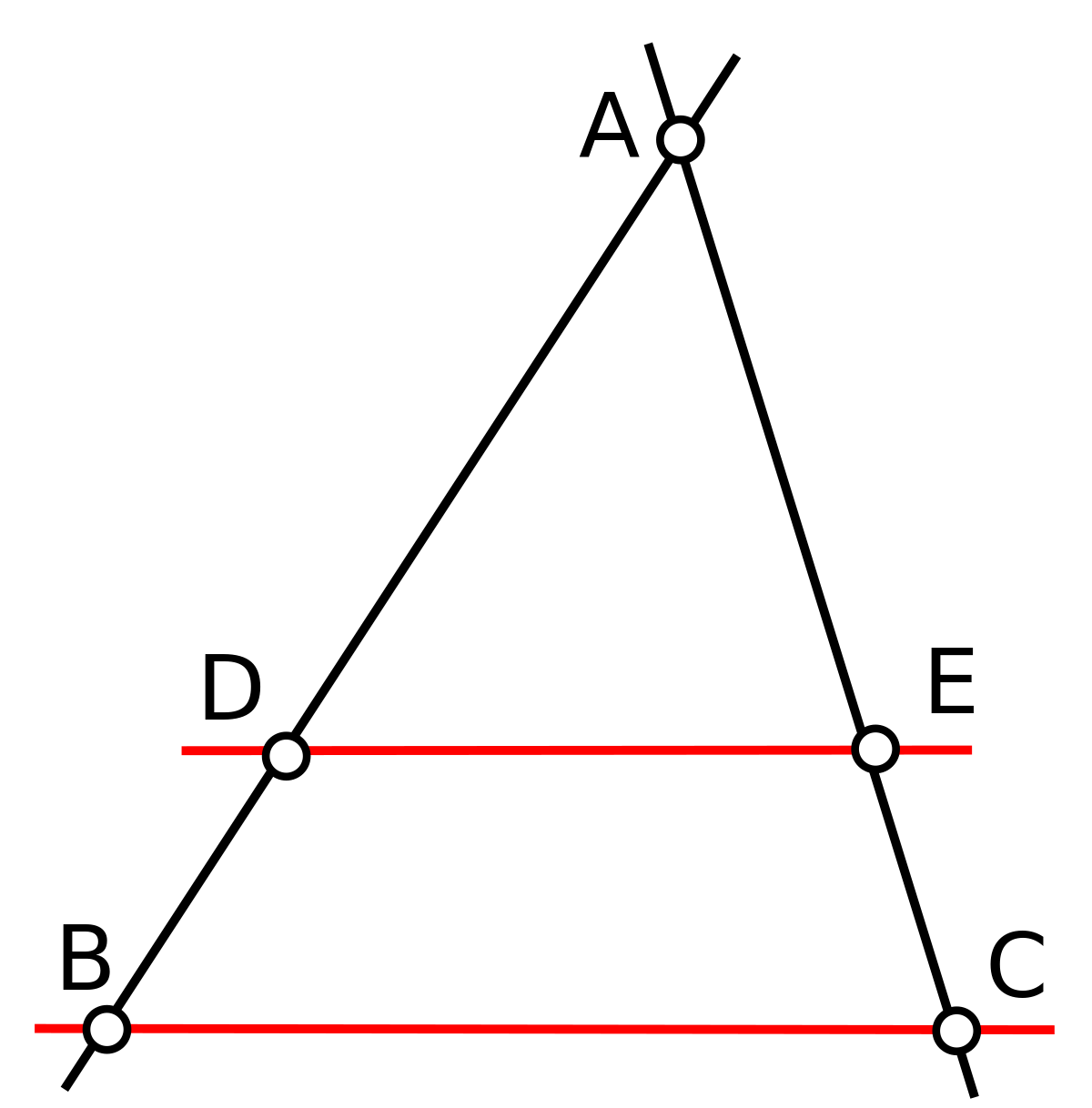
Pour montrer ce résultat, on considère deux droites (noires sur la figure de droite) ayant comme intersection un unique point A. On définit les points B et C tels que la distance AB soit égale à b et AC à c. Les points B et C sont chacun sur une des droites, comme indiqué sur la figure. Le point D (resp. E) se situe sur la droite AB (resp. AC) et la distance AD (resp. AE) est égale à a.b (resp. a.c). Le théorème de Thalès indique que les droites rouges sont parallèles et que :

On peut ré-établir de la sorte toutes les lois régissant les quatre opérations sur les nombres quelconques. Ce travail est réalisé dans le livre VI des Éléments d'Euclide, qui pour cette raison est considéré comme de l'algèbre géométrique.

Toutes les démonstrations proposées dans cet article utilisent le principe de la mesure d'une ou de plusieurs aires. Cette règle est une caractéristique de l'algèbre géométrique et cette démonstration n'est pas une exception. La démonstration d'Euclide du théorème de Thalès se fonde sur le même principe.

Si les démonstrations ou illustrations précédentes sont toujours employées, de par leur simplicité et leur aspect intuitif, une construction rigoureuse des règles opératoires en algèbre, comme réalisée dans le livre VI, ne deviennent ni simples ni intuitifs.