Algèbre géométrique - Définition

Histoire des sciences

Difficultés

Les concepts mathématiques grecs ne sont pas adaptés à un langage algébrique. Cette remarque est particulièrement vraie pour les périodes précoces, comme celle pythagoricienne. Un nombre est une collection de plusieurs unités (un n'est pas un nombre), il correspond chez nous à un entier positif strictement supérieur à un. Un ratio n'est pas un nombre, mais une comparaison de deux grandeurs. La notion de ratio prend un sens à l'aide de la proportion. Quatre grandeurs a, b, c et d sont en proportion si le ratio a:b est égal au ratio c:d. L'unité est une grandeur physique élémentaire, comme une longueur ou une aire qui, associée à des nombres ou des ratios, permet d'exprimer les grandeurs présentes dans une figure géométrique. Dans les mathématiques hellénistiques, il n'existe pas véritablement de multiplication interne. La multiplication de deux longueurs donne l'aire d'une figure plane, la multiplication de deux nombres a et b correspond plus à l'addition itérée a fois du nombre b qu'à une véritable multiplication. La différence entre leurs concepts et notre formalisme complexifie la compréhension des mathématiques grecques. En conséquence, la présentation des idées mathématiques contenues dans cet article est, pour des raisons de simplicité de compréhension, fort loin d'un véritable traité d'époque, comme on le trouve chez Euclide. Par exemple, l'usage du symbole 1 dans la détermination de la section d'extrême et moyenne raison ne ferait pas sens pour un grec.

La deuxième difficulté provient de la rareté des sources avant Platon. Les cinquième et quatrième siècles sont presque vides en terme de traités mathématiques. Le savoir des historiens provient de sources postérieures de plusieurs siècles et pas toujours fiables, d'études précises sur la signification exacte de certains mots, que l'on retrouve aussi dans des textes non mathématiques, d'analyses archéologiques ou encore d'étude des importations d'autres civilisations. À l'aide de ces différentes indications, les historiens reconstruisent les démonstrations possibles et les placent dans leurs époques et leurs écoles respectives. Si, au fil du temps, l'ensemble des indices finit par donner une image cohérente et consensuelle dans les grandes lignes, de nombreux points de divergences, même sur des questions importantes, sont encore présents entre les différents spécialistes.

Usages du terme

Dans son livre de 1902, Zeuthen présente le concept d'algèbre géométrique essentiellement pour décrire le livre II d'Euclide et remarquer qu'il est équivalent à la résolution d'une équation quadratique. Il ne prend pas particulièrement de précautions oratoires ; il prête à Euclide la volonté de : « ... de transporter, aux équations numériquement données, la solution générale trouvée pour les équations quadratiques ». Tannery est convaincu de la véracité des témoignages, nombreux même si souvent tardifs et peu fiables, attribuant la découverte des irrationnels à l'époque de Pythagore. Il pense que ce véritable scandale logique est à l'origine du miracle mathématique grec que sont les Éléments d'Euclide. Or, cette découverte ne peut avoir lieu que dans la mesure où la maîtrise des questions du second degré est suffisante. Ces questions relevant du domaine algébrique, le concept de Zeuthen lui semble fécond, et il l'adopte dès l'année suivante. Pour Tannery, ce qui a limité les grecs dans la démarche n'est pas tant l'absence d'une pensée algébrique qu'un vocabulaire adapté, qu'ils ne possédaient pas : « Ce qui manque aux mathématiciens grecques, ce sont moins les méthodes ... que les formules propres à l'exposition des méthodes ».

Si, à l'image de Heath, cette idée est souvent adoptée par les historiens de l'époque, elle suscite une première polémique dans les années 1920. La forme des mathématiques grecques est géométrique, en extraire une finalité algébrique n'est pas du goût de tous et Jacob Klein s'exprime ainsi : « De plus, la plus part des histoires classiques tentent d'appréhender les mathématiques grecques à l'aide du symbolisme moderne, comme si ce dernier était extrinsèque au contenu mathématique, qui pourrait être habillé sous n'importe quelle forme. ». Parler d'équations chez Euclide, comme le fait Zeuthen, laisse penser que les grecs disposaient déjà d'une inconnue sur lequel ils pouvaient opérer algébriquement, à l'image d'Al-Khawarizmi. Or, une telle démarche n'existe pas avant Diophante.

Otto Neugebauer apporte, dans les années 1940, des arguments en faveur de la thèse de Zeuthen et Tannery. Ses études sur d'autres cultures mathématiques montrent que les grecs de l'époque de Pythagore ont importé des techniques mésopotamiennes. Ce savoir se fonde sur des méthodes et des procédures de calcul (appartenant à la même famille que les fractions continues) permettant d'approximer des racines ou encore des méthodes de résolution de questions du second degré. Cette culture est algébrique, au sens où elle se fonde sur des équivalents d'algorithmes (le mot sera inventé plus tard) dont l'objectif est calculatoire. A l'image de la construction de la section d'extrême et de moyenne raison, de nombreux travaux de l'école de Pythagore sont des traductions de résultats mésopotamiens dans le langage géométrique ionien. Le concept d'algèbre géométrique s'étend à cette branche de savoir, maintenant couverte par l'algèbre et qui se démontre chez les grecques à l'aide de la mesure des aires. On y trouve la théorie des proportions, présente dans les livres V et VI qui décrivent des résultats maintenant contenus dans les axiomes d'un corps commutatif, des méthodes de résolution et d'analyse de la nature d'une solution d'une question de degré 2 présentes dans le livre II, ou encore l'application de l'algorithme d'Euclide à des proportions, dans le livre X, pour démontrer leur incommensurabilité. Elle contient aussi des démonstrations, déjà archaïques à l'époque d'Euclide, comme la théorie du pair et de l'impair.

Jusque dans les années 1970, les historiens n'hésitent plus à s'appuyer sur le concept de Zeuthen et Tannery, même si certains comme Knorr utilisent des précautions oratoires. La polémique est alors relancée. Unguru remarque l'existence d'un schéma ordinaire, présent chez les chinois, les indiens, les arabes ou encore les européens, qui démarrent tous par de la géométrie pour atteindre, après un certain degré d'abstraction, une formalisation plus algébrique. Le schéma chez les grecs serait alors inverse; à partir d'une conception d'orientation algébrique, héritée des mésopotamiens, ils se seraient dirigés vers un système géométrique. Unguru n'imagine pas ce schéma réaliste. Cette position, qui imposerait selon lui une réécriture profonde de l'histoire des mathématiques grecques, est suivie par d'autres historiens comme Szabó.

La réplique est fournie par plusieurs spécialistes dont Van der Waerden qui estime que Szabó attache une importance trop forte au formalisme et que le propre des méthodes pythagoriciennes exposées ici sont de nature calculatoires et algorithmiques et qu'ils sont bien hérités des babyloniens. Mahoney, qui partage la même opinion que Van der Waerden, remarque que les mathématiciens fondateurs de l'algèbre, comme Al-Khawarizmi ou Viète s'inspire largement des textes d'Euclide pour bâtir leurs théories.

Malgré la polémique, de nombreux spécialistes comme Burkert, Itard ou Caveing font usage du concept. Si des historiens généralistes l'utilisent aussi pour des ouvrages de vulgarisation, l'expression est souvent attachée à une mise en garde comme : « Le terme d'algèbre pour une époque où la recherche de l'inconnue n'est pas encore explicite, et encore moins l'étude des "équations", doit être utilisé avec prudence ». L'usage du terme d'algèbre pour des mathématiques anciennes n'est pas tombé en désuétude. Si l'usage de l'expression algèbre géométrique dépasse parfois en histoire des sciences le contexte grec, le cas est suffisamment rare pour mériter d'être noté.

Héritage

La tablette YBC 7289 montre la connaissance d'un algorithme pour extraire la racine de deux.

Si l'histoire de l'algèbre géométrique commence avec Pythagore, comme l'indique Maurice Caveing : « ... il y a des raisons de penser que la mathématique grecque n'est pas née, comme la fille de Métis, tout armée de la tête de Zeus ». Pour cet auteur, l'école pythagoricienne hérite à la fois de l'école ionnienne avec les travaux de Thalès de Milet et du patrimoine égyptien et mésopotamien. Les travaux de l'école de Thalès modifient déjà l'orientation des mathématiques grecques. Elle introduit la notion de preuve. Elles n'étaient surement pas aussi sophistiquées que celles que l'on trouve chez Euclide, cependant cette spécificité grec est déjà présente, les différenciant de leurs prédécesseurs. Une deuxième spécificité des mathématiques ioniennes est son inclinaison à la géométrie. Les résultats prêtés à cette école sont, par exemple, le fait qu'un triangle isocèle possède deux angles égaux ou qu'un triangle de base le diamètre d'un cercle et dont le dernier sommet est situé sur le cercle est rectangle.

A la différence des ioniens, la culture mésopotamienne est, à défaut d'être qualifiée d'algébrique, algorithmique. Les différentes tablettes qui nous sont parvenus montrent une mathématique sous forme de problèmes à résoudre. Celle notée BM 13901, qui contient 24 questions du second degré, laisse penser à une aide géométrique pour guider dans l'algorithme utilisé. La tablette YBC 7289 montre la connaissance du résultat de l'algorithme décrit dans cet article pour la découverte de l'irrationnalité de la section d'extrême et de moyenne raison, mais cette fois ci appliqué à la diagonale d'un carré. Tous les ingrédients pour découvrir l'irrationnalité sont présents.

École pythagoricienne

L'école pythagoricienne cultive le culte du secret, à propos de son savoir. Il est donc difficile dans connaître exactement la teneur, de dater précisément et d'associer un nom aux différents progrès. C'est néanmoins à cette école que l'on doit la naissance de l'algèbre géométrique grec. Cette école hérite du savoir babylonien, ainsi que de l'orientation vers la géométrie et les démonstrations des ioniens. Cette fusion des savoirs apporte un résultat nouveau : l'algèbre géométrique qui, à cette époque se limite encore largement à de l'arithmétique géométrique.

Une démonstration élémentaire d'un cas particulier du théorème de Pythagore.

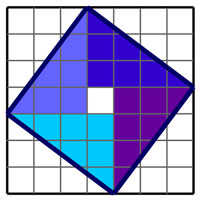
La science mésopotamienne apporte la puissance du calcul. Elle permet en géométrie un progrès que n'avait probablement jamais réalisé les égyptiens ou les mésopotamiens. Un exemple est donné par les premières démonstrations partielles du théorème de Pythagore, que l'on attribue généralement à cette époque. Elle ne s'applique que dans le cas où les côtés sont commensurables — c'est à dire où le triangle correspond à triplet pythagoricien — et utilise un quadrillage typique de l'arithmétique géométrique, illustré sur la figure de gauche. Dans cet exemple on cherche à trouver l'aire du carré en divers bleus, de coté l'hypoténuse d'un triangle rectangle, dont les autres côtés sont de longueurs 3 et 4. Le regroupement deux à deux des triangles intérieurs au carré bleu permet de conclure.

La puissance de la démarche les amène à l'appliquer dans des cas de longueurs incommensurables, sans nécessairement avoir conscience d'une possible incommensurabilité. La construction du pentagone impose la détermination de la section d'extrême et de moyenne raison, qui correspond à une question du deuxième degré. Les procédures calculatoires mésopotamiens sont à même de venir à bout de cette difficulté. Cette construction est probablement réalisée à l'époque de Pythagore. Elle illustre l'orientation grec, le résultat n'est pas une fraction approchant la valeur recherchée, mais une construction géométrique exacte.

La plus importante découverte souvent attribuée aux pythagoriciens et à l'algèbre géométrique est celle des incommensurables. Les éléments étaient déjà presque présents chez les babyloniens, qui pourtant n'en ont jamais parlé. C'est probablement une attitude plus spéculative et moins pragmatique chez les grecs qui fait la différence. Les mésopotamiens concevaient néanmoins aussi les mathématiques comme une spéculation, comme le montre la tablette du illustrée au paragraphe précédent. Elle donne la racine de deux avec une précision de cinq décimales, ce qui n'a aucun intérêt pratique au vu de leur technologie. Cependant les mésopotamiens ont choisi une numération à notation positionnelle, un peu à l'image de notre notation décimale. Si cette notation est plus pratique pour les sciences de l'ingénieur, elle est moins adaptée que l'écriture fractionnaire des grecs pour un travail théorique sur l'irrationnalité. Une valeur dont la notation positionnelle ne se termine pas, comme 0,11111..., ne signifie en rien un caractère irrationnel.

De Pythagore à Euclide

L'école de Pythagore fournit un savoir encore loin de celui que l'on trouve, en matière d'algèbre géométrique, dans les Éléments d'Euclide. Pour atteindre ce but, on peut ranger les difficultés en trois catégories.

La première série de difficultés est d'ordre logique. La découverte des irrationnels montre l'existence de suites dont le comportement ne semble faire guère de sens. Celle donnée en exemple dans l'article n'est pas la plus étudiée, les grecs lui préfèrent celle associée à la diagonale du carré. Elle s'obtient par un processus plus simple et dispose des mêmes propriétés. Cette suite de proportions semble difficilement compatible avec l'hypothèse que tout couple de longueurs est commensurable. Si elle s'approche de plus en plus de la proportion recherchée, elle ne l'atteint jamais. Beaucoup ont vu dans le Paradoxe d'Achille et de la tortue une étude logique issue d'une réflexion sur les suites issues du calcul des incommensurables, c'est à dire une suite qui s'approche infiniment de sa cible, sans jamais la toucher. L'absence de fondement logique suffisant aurait conduit Zénon d'Élée à condamner le raisonnement pythagoricien. Pour trancher de manière fiable ce scandale logique, pour reprendre l'expression de Tannery, il a fallu bâtir une logique consistante. A l'époque d'Aristote, le travail était fait. Ses analytiques exposent clairement comment articuler un raisonnement par l'absurde sans risque d'erreur. Cet auteur utilise plusieurs fois l'exemple du fait que la diagonale d'un carré n'est pas commensurable avec son côté.

La deuxième série de difficultés concerne la modification du cadre conceptuel, imposée par les incommensurables. A l'époque de Pythagore, le théorème qui porte son nom est une égalité entre des nombres — toujours entiers chez les grecs —; chez Euclide, ce théorème est une égalité entre des aires, qui n'ont cette fois-ci aucune raison de pouvoir être représentée par des nombres. Cette modification impose une reconstruction totale de la mathématique, la démonstration du théorème de Thalès doit aussi être revue ainsi que toutes les démonstrations qui doivent maintenant quitter leur gangue commensurable et ne peuvent plus s'appuyer sur une logique fondée sur l'arithmétique géométrique. Maîtriser les incommensurables suppose aussi une arithmétique plus forte, pour mener à bien le raisonnement présenté pour la découverte des irrationnels. Chez Euclide, le raisonnement qui montre que dans le cas de grandeurs commensurables l'algorithme s'arrête, est devenu rigoureux. Il a néanmoins quitté son origine d'arithmétique géométrique, cet algorithme ne fournit plus l'unité de la figure (c'est à dire la plus grande unité qui permet d'exprimer les deux longueurs comme des multiples de l'unité) mais le plus grand commun diviseur entre deux nombres. L'historien Itard s'exprime ainsi à propos de la théorie des nombres chez Euclide : « Elle est à peu près totalement dégagée de l'arithmo-géométrie, de la numération pratique et de la logistique, mais reste étroitement liée à la théorie des rapports ».

Enfin, la troisième série de difficultés consiste à développer les outils permettant de comprendre le comportement asymptotique de l'étrange suite des origines de la découverte. D'une manière ou d'une autre, elle impose une certaine maîtrise du phénomène de limite, qui est alors traitée par l'exhaustion. Le Livre V des éléments permet de construire un univers admettant les incommensurables et les phénomènes de convergence, tout en conservant les propriétés algébriques exprimées maintenant sous forme d'axiomes comme la distributivité de la multiplication par rapport à l'addition dans le corps des réels. Ce travail n'est pas sans conséquences, il impose ce qui deviendra l'axiome d'Archimède et permettra de fonder solidement l'argument de la descente infinie.

L'algèbre géométrique chez Euclide

Deux siècles séparent Pythagore et Euclide. A certains égards, la finalité n'a pas évoluée. On y trouve toujours les méthodes prouvant les propriétés algébriques des proportions, comme la distributivité présentes dans les livres V et VI, les procédures de résolution de questions du second degré et l'usage de l'anthyphérèse — équivalent à une fraction continue — au livre X pour établir l'incommensurabilité de certaines proportions. A d'autres égards, la théorie est métamorphosée. Elle s'appuie sur une logique axiomatisée, la théorie des proportions prend en compte les incommensurables et l'arithmétique utilisée n'a plus grand chose à voir avec celle de Pythagore. En conséquence, toutes les pistes de démonstrations présentées dans cet article sont explorées rigoureusement avec succès et les paradoxes n'en sont plus. Si l'arithmétique géométrique de Pythagore découvre les incommensurables, l'algèbre géométrique d'Euclide les maîtrise. Le grand absent reste le nombre qui se limite encore aux entiers. Eudoxe ne peut pas définir l'axiome d'Archimède, tel que nous l'imaginons aujourd'hui. Cet axiome dépend de la grandeur considérée et le mathématicien ne traite finalement que le cas des aires

Si les fondamentaux introduits à l'époque de Pythagore restent emprunts de l'origine mésopotamienne, la finalité est modifiée. Un algorithme comme l'anthyphérèse maintenant appelé fraction continue ne sert pas, à l'instar de la Mésopotamie, à approximer une proportion, mais à établir la propriété d'incommensurabilité. Le mépris des calculs pour les grecs est notoire, Hérodote est arrêté par une division par 48. Pour Szabó cette modification de finalité n'est pas le plus important. Il n'existe aucun formalisme algébrique chez les grecs et le fait que l'objet principal d'étude soit une proportion et non pas un nombre n'est guère un facteur favorable. Cet absence de formalisme algébrique est la preuve d'une orientation géométrique, loin des préoccupations et des idées d'un précurseur en algèbre comme Diophante. Chez Euclide, l'idée d'équation n'apparaît pas et ne peut apparaître. Opérer sur une inconnue et non plus uniquement des nombres, n'est ici guère envisageable. Pourtant, l'équation et son inconnue sont souvent considérées comme l'acte de naissance de l'algèbre.

Pour Van der Waerden, le propre de l'algèbre est la mise en évidence et l'usage d'une structure. Le travail d'Eudoxe consiste à assurer l'existence d'un monde aux propriétés algébriques, comme la distributivité ou la commutativité d'une multiplication de proportions, tout en respectant une relation d'ordre. Cette question est fondamentalement algébrique et le fait qu'Eudoxe trouve un résultat équivalent aux coupures de Dedekind n'est pas le fruit du hasard, ils cherchent tous deux à résoudre la même question, indépendamment du vêtement ou du formalisme choisi et la matière mathématique reste la même. De même, Le livre II établit les propriétés couramment appelées identités remarquables. Elles sont valables dans tous les anneaux commutatifs et donc celui des proportions géométriques des grecs Le fait de travailler dans une structure à vocation géométrique ne modifie en rien leur nature algébrique. L'usage chez les grecs de l'anthyphérèse a pour objectif une classification des incommensurables. Cette idée, qui sera poussée beaucoup plus loin dans la théorie de Galois, est aussi une question algébrique. En conclusion et pour Van der Waerden, si la finalité et le formalisme sont géométriques, la nature même de l'algèbre géométrique reste inchangée depuis la Mésopotamie.

Pour les fondateurs de l'algèbre arabe et européenne, l'algèbre géométrique s'avère indispensable. La logique de la résolution d'une équation par Al-Khawarizmi n'est possible que dans la mesure où les propriétés algébriques de l'ensemble dont sont issus les coefficients du polynôme sont établies. Dans son traité Abrégé du calcul par la restauration et la comparaison, Al-Khawarizmi s'appuie sur Euclide pour établir la pertinence de la démarche, tout comme son disciple Abu Kamil. Le livre V est le seul à proposer une construction algébrique suffisamment solide pour représenter la structure des nombres réels positifs. Euclide, ne disposant pas de manière pour exprimer les incommensurables, développe dans un langage géométrique un équivalent des identités remarquables — au sens de Van der Waerden — de manière générique. Cette généricité est indispensable pour les premiers algébristes arabes qui ne disposent pas de paramètre et doivent se contenter d'illustrer leurs principes sur des exemples. Au XVI^e siècle en Europe, Viète comble cette lacune et développe le concept du paramètre, généralisant l'algèbre et autorisant l'expression de résultats plus puissants, comme les relations entre coefficients et racines. Pour Viète, la construction de l'algèbre géométrique reste indispensable. Ainsi, pendant près de 2000 ans, l'algèbre géométrique est un outil incontournable pour les algébristes européens et arabes. Cet élément convainc Mahoney du caractère algébrique de la théorie.