Algèbre géométrique - Définition

Arithmétique géométrique

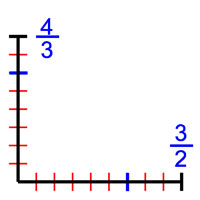
A l’aube des mathématiques grecques et jusqu’au mathématicien Pythagore, l’on pensait que toutes les longueurs pouvaient s’exprimer par ce que l’on appelle maintenant des fractions, ce que l'historien Paul Tannery exprime de la manière suivante : « les Pythagoriciens sont partis de l’idée, naturelle à tout homme non instruit, que toute longueur est nécessairement commensurable à l’unité. ». Ces mathématiciens en conclurent que, pour étudier une figure géométrique, l'on pouvait toujours choisir une longueur unité telle que tous les segments représentés sur la figure aient des longueurs qui s’expriment comme des nombres entiers. La figure de droite illustre cette situation. Elle représente deux segments de longueur 4/3 et 3/2, si l'unité choisie est indiquée par la graduation bleue. L'unité de la graduation rouge est de longueur le sixième de la bleue, avec la graduation rouge, les longueurs sont entières et égales à 8 et 9.

Cette remarque et certaines figures géométriques permettent d’établir des résultats sur les nombres entiers, résultats qui entrent dans la branche mathématique appelée arithmétique. Zeuthen considère ces techniques comme de l’arithmétique géométrique. Il estime que c'est une branche de l’algèbre géométrique car les démarches sont analogues^,,.

Pour faire de l'arithmétique géométrique les représentations sont de même nature que celle du paragraphe Nombre entier, mais il est possible de les simplifier. Les grecs avaient remarqué que tracer les rectangles était inutile. Les pastilles à l’intérieur des carrés, qui étaient alors des galets, suffisaient. La méthode consiste à représenter un nombre à l'aide d'un assemblage de pastilles selon une figure géométrique. L'association du nombre et de la figure est appelée un nombre figuré. Celle utilisée au paragraphe précédent pour représenter 12 est appelée nombre rectangle. Il existe plusieurs figures cataloguées.

Somme des premiers nombres

L'objectif ici consiste à sommer les premiers nombres entiers, par exemple ceux de 1 à 8. Cela revient à calculer 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8. Pour cela, on les assemble comme les pastilles rouges du schéma de droite. On construit une autre figure semblable à l'aide de pastilles bleues et on assemble les deux figures à la manière du schéma. On en déduit que le double de la somme recherchée est égale à l’aire d’un rectangle de base 9 et de hauteur 8 c'est-à-dire 72. La somme recherchée est égale à la moitié de 72, c'est-à-dire 36. Dans le cas général, la somme des entiers de 1 à n est égale à :

La figure de droite illustre la raison pour laquelle ces sommes sont appelées par les grecs des nombres triangulaires. L'association d'un nombre comme 9 x 8 à rectangle de base d'une unité supérieure à sa hauteur est appelée un nombre oblong.

Nombre carré

Un nombre carré est un nombre égal à un certain entier multiplié par lui-même. Par exemple, 9 est un nombre carré car 3 x 3 = 9. Il se présente de manière figurée comme un carré. Pour établir la liste des premiers carrés, l’arithmétique géométrique peut être utile. On suppose, par exemple, connue la liste jusqu’à 7 x 7 = 49. Pour trouver la valeur du carré suivant, de côté 8, on raisonne à l’aide de la figure de gauche. Le nombre 8 x 8 peut être vu comme la somme de 7 x 7 correspondant aux billes rouges, de 7 correspondant aux billes vertes et 8 correspondant aux billes bleues. De manière générale, on dispose de l’égalité :

Établir la liste des premiers nombres carrés est un vieil exercice, déjà réalisé par les mésopotamiens. A cette époque, la numération était en base 60. Réaliser des multiplications comme nous le faisons maintenant aurait supposé d’apprendre les tables de multiplication jusqu’à 60, exercice de mémorisation difficile et que l’on n'imposait pas aux écoliers mésopotamiens. Les tables de carrés, qui existaient alors, étaient bien utiles. Par exemple, la multiplication de 15 par 29 donne :

Les grecs héritèrent du savoir mésopotamien et ajoutèrent leur propre interprétation qui leur permit de trouver d’autres résultats. Ils avaient remarqué que, si le côté d'un nombre carré est pair, le nombre carré l'est aussi, car il se décompose en la somme de deux nombres rectangles égaux dont la base est égale à deux fois la hauteur. La logique géométrique permet de comprendre que si le côté est de longueur impair, l’aire l’est aussi. La figure de droite l’illustre sur l’exemple 15 x 15. La représentation du nombre carré montre qu’il est somme d’un carré, en rouge sur la figure, qui est pair (il est composé d’autant de pastilles claires que foncées), d’un nombre pair (les pastilles bleues, qui sont graphiquement divisées en deux parties égales) et d’une pastille verte, isolée. Ainsi 15 x 15 est la somme d’un nombre pair (les pastilles rouges et les bleues) et de 1, ce qui est un nombre impair.

Triplet pythagoricien

À l’aide de la figure permettant de calculer la liste des carrés, les grecs définirent un nouveau nombre figuré, le nombre gnomon. Les pastilles bleues de la figure de gauche correspondent à un nombre gnomon : 9. Cette figure de gauche montre qu’un carré est formé d'une suite de nombres gnomons, correspondant à la suite des premiers nombres impairs. Ce que l’on peut encore traduire par l’égalité :

Ce résultat permet de construire des triplets pythagoriciens si, comme sur la figure de gauche, le dernier gnomon est un carré parfait. L’égalité issue cette figure s’écrit :

Or la somme des nombres entre parenthèses correspond à un nombre carré ; l’égalité s’écrit encore :

Cette observation permet de construire des séries de trois nombres a, b et c, vérifiant a² + b² = c², que l’on appelle triplet pythagoricien. À l'aide du théorème de Pythagore, il devient possible de construire des triangles rectangles (à côtés entiers). Si, au lieu de choisir une largeur 1 pour le gnomon, on lui attribue une largeur quelconque, on peut trouver une méthode qui donne tous les triplets pythagoriciens. Elle est proposée dans le livre X des Éléments d'Euclide.

Somme des cubes

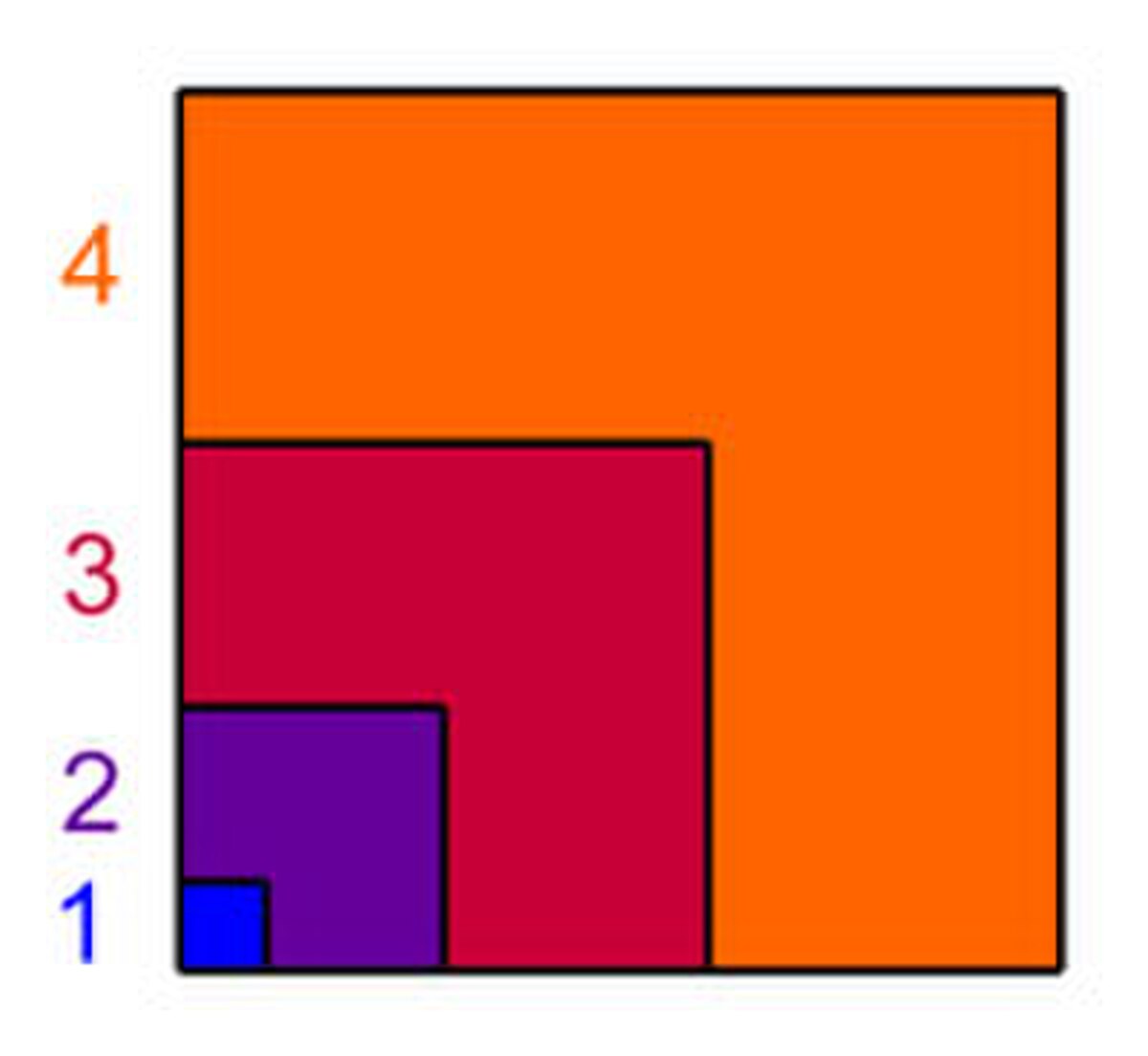
Les nombres cubiques sont construits comme les carrés, à la différence que cette fois-ci le nombre représente le volume et non la surface. Les premiers nombres cubiques sont 1 =  1³, 8 =  2³, 27 =  3³, 64 =  4³ … Le raisonnement suivant permet de comprendre pourquoi la somme des premiers nombres cubiques est toujours un nombre carré.

Le carré de droite possède un côté de longueur un nombre triangulaire, ici 10, égal à 1 + 2 + 3 + 4. Ce carré est décomposé en une somme de gnomons dont la largeur vaut 1 puis 2 puis 3 puis 4. Calculons la surface du dernier gnomon. Il contient un rectangle de base 10 et de largeur 4 soit d’aire 40. Si l’on considère qu’il est composé de deux rectangles ayant cette géométrie, on compte deux fois un carré de coté 4. Autrement dit, l’aire du gnomon est égal à 2 x 40 - 4². Cette aire est encore égale à 64 c'est-à-dire le cube de 4.

Ce raisonnement est vrai pour tous les nombres gnomons de la figure. Considérons le n^ième nombre gnomon, le raisonnement précédent montre qu'il est égal à :

On en déduit que la somme des n premiers nombres cubiques est un nombre carré de côté le n^ième nombre triangulaire. Cette fois-ci, à la différence des exemples précédents, rien n’indique que les grecs de l'époque de Pythagore connaissaient cette démonstration. Soit ils ne la connaissaient pas, soit ils n'ont pas jugés utile de laisser une trace encore visible de leur démonstration. La preuve présentée ici est attribuée à un mathématicien arabe : Al-Karaji.